
Standing waves are produced in \[10m\] long stretched strings. If the string vibrates in 5 segments and wave velocity is \[20m{s^{ - 1}}\] , then its frequency will be
A. \[5Hz\]
B. \[2Hz\]
C. \[10Hz\]
D. \[12Hz\]
Answer
442.2k+ views
Hint: To answer the question, we will build a simple diagram based on the question. The entire length of the string is \[10m\] , and there are five segments, so we will compute the length of one segment and determine the value of $\lambda $ , and then calculate the frequency $(\nu )$ using this $\lambda $ .
Complete answer:
Before we go into the question, let's have a look at what a standing wave is. The combination of two waves flowing in opposite directions, each with the same amplitude and frequency, is known as a standing wave.
Now, let us come to the question;
The wavelength of a stretched string's fundamental vibrational mode is twice the length of the string.
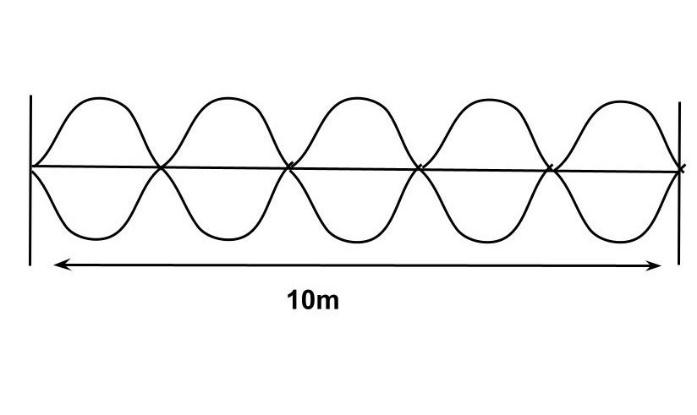
Because the string produces standing waves and vibrates in five parts, it can be shown as
\[\therefore 5\dfrac{\lambda }{2} = 10\]
Therefore, from here we will find value of $\lambda $
\[ \Rightarrow \lambda = 4{\mkern 1mu} m\]
The wave's velocity, \[v\] , is given to us in the question as $v = 20m{s^{ - 1}}$
Hence, the frequency will be \[\nu = \dfrac{v}{\lambda } = \dfrac{{20}}{4} = 5{\mkern 1mu} {s^{ - 1}} = 5{\mkern 1mu} Hz\]
Therefore, the frequency is \[5Hz\]
The correct option is: (A) \[5Hz\]
Note:
It's important to note that standing waves don't just appear out of nowhere. They call for energy to be delivered into a system at a specific frequency. That is, when a system's driving frequency is identical to its natural frequency. Resonance is the term for this situation. Standing waves are invariably linked to resonance.
Complete answer:
Before we go into the question, let's have a look at what a standing wave is. The combination of two waves flowing in opposite directions, each with the same amplitude and frequency, is known as a standing wave.
Now, let us come to the question;
The wavelength of a stretched string's fundamental vibrational mode is twice the length of the string.

Because the string produces standing waves and vibrates in five parts, it can be shown as
\[\therefore 5\dfrac{\lambda }{2} = 10\]
Therefore, from here we will find value of $\lambda $
\[ \Rightarrow \lambda = 4{\mkern 1mu} m\]
The wave's velocity, \[v\] , is given to us in the question as $v = 20m{s^{ - 1}}$
Hence, the frequency will be \[\nu = \dfrac{v}{\lambda } = \dfrac{{20}}{4} = 5{\mkern 1mu} {s^{ - 1}} = 5{\mkern 1mu} Hz\]
Therefore, the frequency is \[5Hz\]
The correct option is: (A) \[5Hz\]
Note:
It's important to note that standing waves don't just appear out of nowhere. They call for energy to be delivered into a system at a specific frequency. That is, when a system's driving frequency is identical to its natural frequency. Resonance is the term for this situation. Standing waves are invariably linked to resonance.
Recently Updated Pages
Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is the opposite of entropy class 11 chemistry CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




