
How do you solve the equation \[{x^2} - 2x - 24 = 0\] by graphing?
Answer
525.3k+ views
Hint: Here, we will first find the \[x\] and \[y\] intercepts and the vertex to plot the graph of this equation. As this is a quadratic equation, its graph will be U-shaped. After plotting the graph, we will observe what are the possible values of \[x\] when \[y = 0\] to find the required solution using the graph.
Complete step-by-step answer:
The given quadratic equation is: \[{x^2} - 2x - 24 = 0\]
Now, in order to plot a graph of this equation, we will, first of all, determine the \[y\] intercept.
Hence, we will substitute \[x = 0\]
Hence, \[y = f\left( 0 \right) = {\left( 0 \right)^2} - 2\left( 0 \right) - 24 = - 24\]
Thus, the \[y\] intercept is \[\left( {0, - 24} \right)\]
Now, we will determine the \[x\] intercept, by substituting \[y = f\left( x \right) = 0\]
\[{x^2} - 2x - 24 = 0\]
Doing middle term split, we get
\[ \Rightarrow {x^2} - 6x + 4x - 24 = 0\]
\[ \Rightarrow x\left( {x - 6} \right) + 4\left( {x - 6} \right) = 0\]
Factoring out common terms, we get
\[ \Rightarrow \left( {x + 4} \right)\left( {x - 6} \right) = 0\]
By using zero product property, we get
\[\begin{array}{l} \Rightarrow \left( {x + 4} \right) = 0\\ \Rightarrow x = - 4\end{array}\]
Or
\[\begin{array}{l} \Rightarrow \left( {x - 6} \right) = 0\\ \Rightarrow x = 6\end{array}\]
Therefore, for \[y = 0\], we get two \[x\] intercepts, i.e. \[\left( { - 4,0} \right)\] and \[\left( {6,0} \right)\]
Now, we will determine the vertex by using the formula \[x = \dfrac{{ - b}}{{2a}}\] to find the \[x\]-value of the vertex and then, we will substitute this value in the function to find the corresponding value of \[y\].
In the given equation, \[{x^2} - 2x - 24 = 0\] by comparing it to \[a{x^2} + bx + c = 0\], we get,
\[a = 1\], \[b = - 2\] and \[c = - 24\]
Thus, substituting these values in \[x = \dfrac{{ - b}}{{2a}}\], we get,
\[x = \dfrac{{ - \left( { - 2} \right)}}{{2\left( 1 \right)}} = \dfrac{2}{2} = 1\]
Substituting this is the equation \[y = {x^2} - 2x - 24\], we get,
\[y = {1^2} - 2\left( 1 \right) - 24\]
Simplifying the expression, we get
\[ \Rightarrow y = 1 - 2 - 24 = - 25\]
Therefore, the vertex is: \[\left( {1, - 25} \right)\]
Also, let us substitute \[x = 2\] in the \[y = {x^2} - 2x - 24\] thus, we get,
\[y = {2^2} - 2\left( 2 \right) - 24\]
Simplifying the expression, we get
\[ \Rightarrow y = 4 - 4 - 24 = - 24\]
Therefore, the other point is \[\left( {2, - 24} \right)\]
Hence, we will plot the graph having:
\[y\] intercept as \[\left( {0, - 24} \right)\]
\[x\] intercepts as \[\left( { - 4,0} \right)\] and \[\left( {6,0} \right)\]
Vertex: \[\left( {1, - 25} \right)\]
Extra point: \[\left( {2, - 24} \right)\]
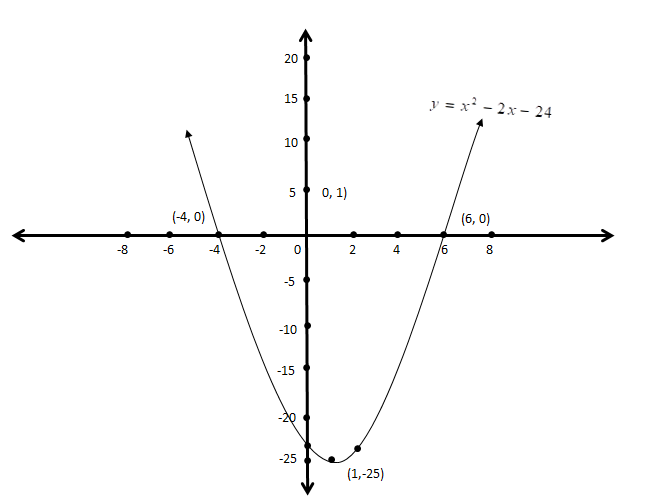
Hence, from this graph, we can clearly observe that the values \[x = - 4\]and \[x = 6\] when \[y = 0\]
Therefore, this is the required solution of the given equation \[{x^2} - 2x - 24 = 0\] by graphing.
Hence, this is the required answer.
Note:
An equation is called a quadratic equation if it can be written in the form of \[a{x^2} + bx + c = 0\] where \[a,b,c\] are real numbers and \[a \ne 0\] , as it is the coefficient of \[{x^2}\] and it determines that this is a quadratic equation. Also, the power of a quadratic equation will be 2 as it is a ‘quadratic equation’. Also, a quadratic equation will give us two roots and its graph is U-shaped as we can observe from this question.
Complete step-by-step answer:
The given quadratic equation is: \[{x^2} - 2x - 24 = 0\]
Now, in order to plot a graph of this equation, we will, first of all, determine the \[y\] intercept.
Hence, we will substitute \[x = 0\]
Hence, \[y = f\left( 0 \right) = {\left( 0 \right)^2} - 2\left( 0 \right) - 24 = - 24\]
Thus, the \[y\] intercept is \[\left( {0, - 24} \right)\]
Now, we will determine the \[x\] intercept, by substituting \[y = f\left( x \right) = 0\]
\[{x^2} - 2x - 24 = 0\]
Doing middle term split, we get
\[ \Rightarrow {x^2} - 6x + 4x - 24 = 0\]
\[ \Rightarrow x\left( {x - 6} \right) + 4\left( {x - 6} \right) = 0\]
Factoring out common terms, we get
\[ \Rightarrow \left( {x + 4} \right)\left( {x - 6} \right) = 0\]
By using zero product property, we get
\[\begin{array}{l} \Rightarrow \left( {x + 4} \right) = 0\\ \Rightarrow x = - 4\end{array}\]
Or
\[\begin{array}{l} \Rightarrow \left( {x - 6} \right) = 0\\ \Rightarrow x = 6\end{array}\]
Therefore, for \[y = 0\], we get two \[x\] intercepts, i.e. \[\left( { - 4,0} \right)\] and \[\left( {6,0} \right)\]
Now, we will determine the vertex by using the formula \[x = \dfrac{{ - b}}{{2a}}\] to find the \[x\]-value of the vertex and then, we will substitute this value in the function to find the corresponding value of \[y\].
In the given equation, \[{x^2} - 2x - 24 = 0\] by comparing it to \[a{x^2} + bx + c = 0\], we get,
\[a = 1\], \[b = - 2\] and \[c = - 24\]
Thus, substituting these values in \[x = \dfrac{{ - b}}{{2a}}\], we get,
\[x = \dfrac{{ - \left( { - 2} \right)}}{{2\left( 1 \right)}} = \dfrac{2}{2} = 1\]
Substituting this is the equation \[y = {x^2} - 2x - 24\], we get,
\[y = {1^2} - 2\left( 1 \right) - 24\]
Simplifying the expression, we get
\[ \Rightarrow y = 1 - 2 - 24 = - 25\]
Therefore, the vertex is: \[\left( {1, - 25} \right)\]
Also, let us substitute \[x = 2\] in the \[y = {x^2} - 2x - 24\] thus, we get,
\[y = {2^2} - 2\left( 2 \right) - 24\]
Simplifying the expression, we get
\[ \Rightarrow y = 4 - 4 - 24 = - 24\]
Therefore, the other point is \[\left( {2, - 24} \right)\]
Hence, we will plot the graph having:
\[y\] intercept as \[\left( {0, - 24} \right)\]
\[x\] intercepts as \[\left( { - 4,0} \right)\] and \[\left( {6,0} \right)\]
Vertex: \[\left( {1, - 25} \right)\]
Extra point: \[\left( {2, - 24} \right)\]

Hence, from this graph, we can clearly observe that the values \[x = - 4\]and \[x = 6\] when \[y = 0\]
Therefore, this is the required solution of the given equation \[{x^2} - 2x - 24 = 0\] by graphing.
Hence, this is the required answer.
Note:
An equation is called a quadratic equation if it can be written in the form of \[a{x^2} + bx + c = 0\] where \[a,b,c\] are real numbers and \[a \ne 0\] , as it is the coefficient of \[{x^2}\] and it determines that this is a quadratic equation. Also, the power of a quadratic equation will be 2 as it is a ‘quadratic equation’. Also, a quadratic equation will give us two roots and its graph is U-shaped as we can observe from this question.
Recently Updated Pages
Explain the double helix structure of DNA with a labeled class 10 biology CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE

Which party gave the slogan Save Democracy in the Lok class 10 social science CBSE

iWhat is Rain Water Harvesting iiWhat are the advantages class 10 social science CBSE

Explain any 5 effects of the Russian Revolution of class 10 social science CBSE

Refractive index of glass with respect to water is class 10 physics CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

The uses of bleaching powder are A It is used bleaching class 10 chemistry CBSE

Write any two uses of Plaster of Paris class 10 chemistry CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Discuss the main reasons for poverty in India




