
How do you solve the compound inequality \[h-10 < -21\] or \[h+3 < 2\]?
Answer
468.9k+ views
Hint: This question is from the topic of algebra. In this question, we will first solve the equation $h-10 < -21$ and find the range of h. After that, we will solve the equation $h+3< 2$ and the range of h from the equation. After using both ranges of h, we will take union of both ranges. After taking the union, we will get our answer.
Complete step by step solution:
Let us solve this question.
In this question, we have asked to solve the compound inequality h-10<-21 or h+3<2. Or, we can say we have to find the range of h using these equations.
So, let us first solve the equation
\[h-10<-21\]
Adding 10 to both the side of equation, we can write the above equation as
\[\Rightarrow h-10+10<-21+10\]
The above equation can also be written as
\[\Rightarrow h<-11\]
So, from here we get the range of h is from negative of infinity to negative of 11, that is \[\left( -\infty ,-11 \right)\], where negative of infinity and negative of 11 is not included.
Now, let us solve the equation
\[h+3<2\]
After subtracting 3 to both the side of equation, we can write the above equation as
\[\Rightarrow h+3-3<2-3\]
The above equation can also be written as
\[\Rightarrow h<-1\]
Hence, from here we get that the range of h is from negative of infinity to negative of 1, that is \[\left( -\infty ,-1 \right)\], where negative of infinity and negative of 1 is not included.
Now, we get the two ranges of h. They are \[h\in \left( -\infty ,-11 \right)\] and \[h\in \left( -\infty ,-1 \right)\].
We can see in the question that there is ‘or’ between the inequalities, so we will take union of these two ranges.
Hence, we can write
\[h\in \left( -\infty ,-11 \right)\bigcup \left( -\infty ,-1 \right)\]
We can say that
\[h\in \left( -\infty ,-1 \right)\]
Therefore, we get the range of h as \[h\in \left( -\infty ,-1 \right)\] or we can write
\[h<-1\]
Note: We should have a better knowledge on the topic of algebra to solve this type of question easily. We should know how to find the range of any variable. We should know how to take intersections.
We can solve this question by different methods.
As earlier, we have solved the equations that are \[h-10 < -21\] and \[h+3 < 2\], and found their range as \[h < -11\] and \[h < -1\] respectively.
So, a common range for h can be found by different method which can be seen in the following:
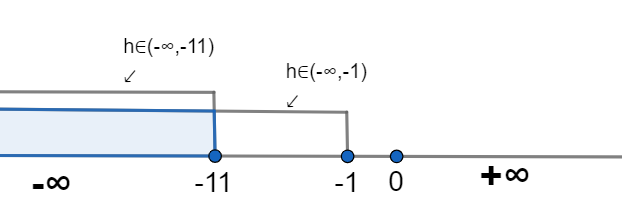
Here, we can see that the common range of h is
\[h < -11\]
Complete step by step solution:
Let us solve this question.
In this question, we have asked to solve the compound inequality h-10<-21 or h+3<2. Or, we can say we have to find the range of h using these equations.
So, let us first solve the equation
\[h-10<-21\]
Adding 10 to both the side of equation, we can write the above equation as
\[\Rightarrow h-10+10<-21+10\]
The above equation can also be written as
\[\Rightarrow h<-11\]
So, from here we get the range of h is from negative of infinity to negative of 11, that is \[\left( -\infty ,-11 \right)\], where negative of infinity and negative of 11 is not included.
Now, let us solve the equation
\[h+3<2\]
After subtracting 3 to both the side of equation, we can write the above equation as
\[\Rightarrow h+3-3<2-3\]
The above equation can also be written as
\[\Rightarrow h<-1\]
Hence, from here we get that the range of h is from negative of infinity to negative of 1, that is \[\left( -\infty ,-1 \right)\], where negative of infinity and negative of 1 is not included.
Now, we get the two ranges of h. They are \[h\in \left( -\infty ,-11 \right)\] and \[h\in \left( -\infty ,-1 \right)\].
We can see in the question that there is ‘or’ between the inequalities, so we will take union of these two ranges.
Hence, we can write
\[h\in \left( -\infty ,-11 \right)\bigcup \left( -\infty ,-1 \right)\]
We can say that
\[h\in \left( -\infty ,-1 \right)\]
Therefore, we get the range of h as \[h\in \left( -\infty ,-1 \right)\] or we can write
\[h<-1\]
Note: We should have a better knowledge on the topic of algebra to solve this type of question easily. We should know how to find the range of any variable. We should know how to take intersections.
We can solve this question by different methods.
As earlier, we have solved the equations that are \[h-10 < -21\] and \[h+3 < 2\], and found their range as \[h < -11\] and \[h < -1\] respectively.
So, a common range for h can be found by different method which can be seen in the following:

Here, we can see that the common range of h is
\[h < -11\]
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
How much is 23 kg in pounds class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

What organs are located on the left side of your body class 11 biology CBSE

What are the similarities and differences between the class 11 biology CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

What is the mass of carbon dioxide which contains the class 11 chemistry CBSE




