
How do you solve and graph the compound inequality $2x-6<-14$ or $2x+3<1$?
Answer
466.5k+ views
Hint: To solve the compound inequality first we separately solve both in equations. Then we will obtain two solutions by solving both equations. Then we plot a graph for each solution. The intersection of both the solutions is the required solution of the given system of equations.
Complete step-by-step solution:
We have been given a system of inequality equations $2x-6<-14$ or $2x+3<1$.
We have to solve and graph the given compound inequality.
First let us consider the equation $2x-6<-14$.
To solve the given equation first we will keep the variable term at the LHS of inequality and shift constant terms at the RHS. Then we will get
$\Rightarrow 2x<-14+6$
Now, simplifying the above obtained equation we will get
$\begin{align}
& \Rightarrow 2x<-8 \\
& \Rightarrow x<\dfrac{-8}{2} \\
& \Rightarrow x<-4 \\
\end{align}$
Now, let us consider the equation $2x+3<1$.
To solve the given equation first we will keep the variable term at the LHS of inequality and shift constant terms at the RHS. Then we will get
$\Rightarrow 2x<1-3$
Now, simplifying the above obtained equation we will get
$\begin{align}
& \Rightarrow 2x<-2 \\
& \Rightarrow x<\dfrac{-2}{2} \\
& \Rightarrow x<-1 \\
\end{align}$
Now, let us plot a graph for $x<-4$ and $x<-1$ then we will get
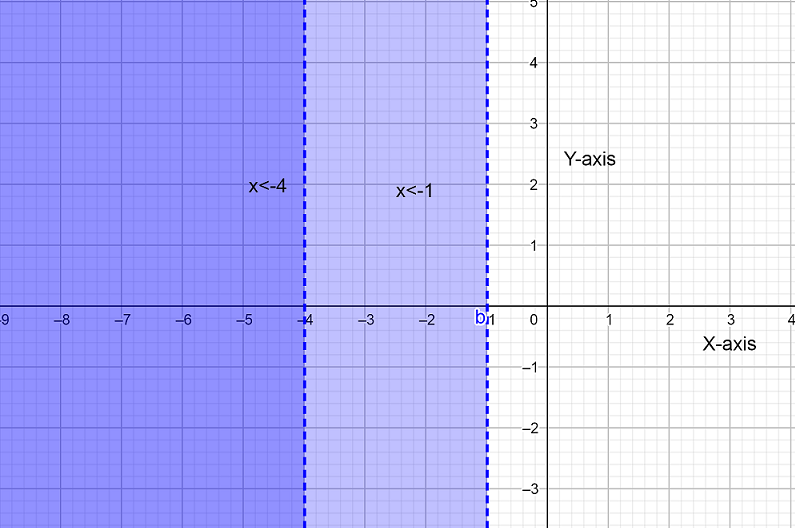
By observing the above graph we reach the conclusion that $x<-4$ is the common solution for both the inequality.
Hence $x<-4$ is the solution of given compound inequality.
Note: The point to be noted is that if we didn’t find any common intersection area by plotting the graph of solutions of two inequalities then there is no solution of the system of linear inequalities. If the equations have “or” then we need to combine two solutions and if the equations have “and” then the solution is where the two graphs overlap.
Complete step-by-step solution:
We have been given a system of inequality equations $2x-6<-14$ or $2x+3<1$.
We have to solve and graph the given compound inequality.
First let us consider the equation $2x-6<-14$.
To solve the given equation first we will keep the variable term at the LHS of inequality and shift constant terms at the RHS. Then we will get
$\Rightarrow 2x<-14+6$
Now, simplifying the above obtained equation we will get
$\begin{align}
& \Rightarrow 2x<-8 \\
& \Rightarrow x<\dfrac{-8}{2} \\
& \Rightarrow x<-4 \\
\end{align}$
Now, let us consider the equation $2x+3<1$.
To solve the given equation first we will keep the variable term at the LHS of inequality and shift constant terms at the RHS. Then we will get
$\Rightarrow 2x<1-3$
Now, simplifying the above obtained equation we will get
$\begin{align}
& \Rightarrow 2x<-2 \\
& \Rightarrow x<\dfrac{-2}{2} \\
& \Rightarrow x<-1 \\
\end{align}$
Now, let us plot a graph for $x<-4$ and $x<-1$ then we will get

By observing the above graph we reach the conclusion that $x<-4$ is the common solution for both the inequality.
Hence $x<-4$ is the solution of given compound inequality.
Note: The point to be noted is that if we didn’t find any common intersection area by plotting the graph of solutions of two inequalities then there is no solution of the system of linear inequalities. If the equations have “or” then we need to combine two solutions and if the equations have “and” then the solution is where the two graphs overlap.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Whales are warmblooded animals which live in cold seas class 11 biology CBSE




