
$P$ and $Q$ are any two points lying on the sides $DC$ and $AD$ respectively of a parallelogram $ABCD$. Show that $area\;\left( {\Delta APB} \right) = area\;\left( {\Delta BQC} \right)$.
Answer
556.2k+ views
Hint:In the solution we will use the concept of parallelogram which states that if the triangle and parallelogram have the same base and parallels then the area of triangle is half of the parallelogram.
Complete step-by-step solution
Given: $P$ and $Q$ are any two points lying on the sides $DC$ and $AD$ respectively of a parallelogram $ABCD$.
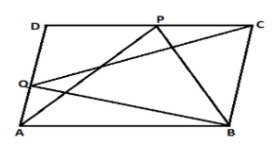
Since $\Delta APB$ and parallelogram $ABCD$ are on the same base $AB$ and between the same parallels.
Therefore, $ar\left( {\Delta APB} \right) = \dfrac{1}{2}ar\left( {{\rm{Parallelogram}}\;\;ABCD} \right)$ …..(1)
Similarly,
Since $\Delta BQC$ and parallelogram $ABCD$ are on the same base $AB$ and between the same parallels.
Therefore, $ar\left( {\Delta BQC} \right) = \dfrac{1}{2}ar\left( {{\rm{Parallelogram}}\;\;ABCD} \right)$ …..(2)
From equation (1) and equation (2) we can say that
$area\;\left( {\Delta APB} \right) = area\;\left( {\Delta BQC} \right)$
Note: Here we have make sure of using the concept of parallelogram instead of concept of quadrilateral.So here we can say that when parallelograms have same base as well as same parallels then the area of parallelogram is doubled of the area of triangle.
Complete step-by-step solution
Given: $P$ and $Q$ are any two points lying on the sides $DC$ and $AD$ respectively of a parallelogram $ABCD$.

Since $\Delta APB$ and parallelogram $ABCD$ are on the same base $AB$ and between the same parallels.
Therefore, $ar\left( {\Delta APB} \right) = \dfrac{1}{2}ar\left( {{\rm{Parallelogram}}\;\;ABCD} \right)$ …..(1)
Similarly,
Since $\Delta BQC$ and parallelogram $ABCD$ are on the same base $AB$ and between the same parallels.
Therefore, $ar\left( {\Delta BQC} \right) = \dfrac{1}{2}ar\left( {{\rm{Parallelogram}}\;\;ABCD} \right)$ …..(2)
From equation (1) and equation (2) we can say that
$area\;\left( {\Delta APB} \right) = area\;\left( {\Delta BQC} \right)$
Note: Here we have make sure of using the concept of parallelogram instead of concept of quadrilateral.So here we can say that when parallelograms have same base as well as same parallels then the area of parallelogram is doubled of the area of triangle.
Recently Updated Pages
How do you convert r6sec theta into Cartesian form class 10 maths CBSE

How do you solve dfrac5y3dfracy+72y6+1 and find any class 10 maths CBSE

If sin A+B1 and cos AB1 0circ le left A+B rightle 90circ class 10 maths CBSE

On the number line 10 is to the of zero class 10 maths CBSE

How do you solve 5xge 30 class 10 maths CBSE

In the following sentence supply a verb in agreement class 10 english CBSE

Trending doubts
Write examples of herbivores carnivores and omnivo class 10 biology CBSE

Search and you will find The speed of light is kms class 10 physics CBSE

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

The speed of revolution of earth in its orbit around class 10 social science CBSE

Difference between mass and weight class 10 physics CBSE

Explain series connections of Resistors and derive class 10 physics CBSE




