
Explain series connections of Resistors and derive the formula of equivalent resistance.
Answer
532.8k+ views
Hint: Resistor is an electrical component that is used to convert the current into the voltage or the voltage into the current. Resistors are said to be in series when they are connected in one line. Here, we will use ohm’s law to calculate the formula of equivalent resistance.
Complete step by step answer:
Consider a circuit carrying a current $I$ in which three resistors are connected in series. A voltage $V$ is connected to the circuit.
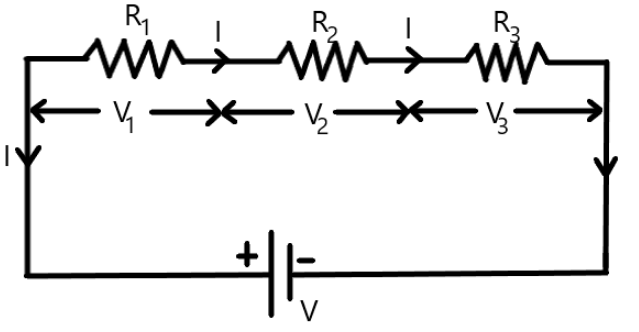
Here, ${R_1}$ , ${R_2}$ and ${R_3}$ are the resistors that are connected in series and ${V_1}$ , ${V_2}$ and ${V_3}$ are the voltage drops across the respective resistors.
Now, as the resistors are connected in series, the current flowing through the circuit will be the same across all the resistors. Now, the voltage $V$ across the circuit is given by
$V = {V_1} + {V_2} + {V_3} + ....$
Now, if a resistor $R$ is placed in the place of these three resistors ${R_1}$ , ${R_2}$ and ${R_3}$ such that the current in the circuit remains the same, then $R$ is called the equivalent resistance.

Therefore, for an equivalent resistance, $V = IR$.
Now, the voltage drop across the resistance ${R_1}$ is ${V_1} = I{R_1}$.
The voltage drop across the resistance ${R_2}$ is ${V_2} = I{R_2}$.
The voltage drop across the resistance ${R_3}$ is ${V_3} = I{R_3}$.
Therefore, the voltage $V$ across the circuit is given by,
$V = {V_1} + {V_2} + {V_3} + .....$
$ \Rightarrow \,V = I{R_1} + I{R_2} + I{R_3}$
Now, taking $I$ common, we get
$V = I\left( {{R_1} + {R_2} + {R_3}} \right)$
$ \therefore \,\dfrac{V}{I} = {R_1} + {R_2} + {R_3}$
Now, as we know $V = IR$
Therefore, $\dfrac{V}{I} = R$
Therefore, the above equation becomes
$R = {R_1} + {R_2} + {R_3}$
Which is the equivalent resistance.
Thus, we can say that the equivalent resistance $R$ in the circuit is the sum of all the individual resistances in the circuit.
Note:All the resistors in the series do not get a source voltage, therefore, they divide the voltage across them. Also, the amount of energy used by the resistors will be the same as the amount of energy used by a single resistor. This energy is also divided across the resistors depending upon their resistances.
Complete step by step answer:
Consider a circuit carrying a current $I$ in which three resistors are connected in series. A voltage $V$ is connected to the circuit.

Here, ${R_1}$ , ${R_2}$ and ${R_3}$ are the resistors that are connected in series and ${V_1}$ , ${V_2}$ and ${V_3}$ are the voltage drops across the respective resistors.
Now, as the resistors are connected in series, the current flowing through the circuit will be the same across all the resistors. Now, the voltage $V$ across the circuit is given by
$V = {V_1} + {V_2} + {V_3} + ....$
Now, if a resistor $R$ is placed in the place of these three resistors ${R_1}$ , ${R_2}$ and ${R_3}$ such that the current in the circuit remains the same, then $R$ is called the equivalent resistance.

Therefore, for an equivalent resistance, $V = IR$.
Now, the voltage drop across the resistance ${R_1}$ is ${V_1} = I{R_1}$.
The voltage drop across the resistance ${R_2}$ is ${V_2} = I{R_2}$.
The voltage drop across the resistance ${R_3}$ is ${V_3} = I{R_3}$.
Therefore, the voltage $V$ across the circuit is given by,
$V = {V_1} + {V_2} + {V_3} + .....$
$ \Rightarrow \,V = I{R_1} + I{R_2} + I{R_3}$
Now, taking $I$ common, we get
$V = I\left( {{R_1} + {R_2} + {R_3}} \right)$
$ \therefore \,\dfrac{V}{I} = {R_1} + {R_2} + {R_3}$
Now, as we know $V = IR$
Therefore, $\dfrac{V}{I} = R$
Therefore, the above equation becomes
$R = {R_1} + {R_2} + {R_3}$
Which is the equivalent resistance.
Thus, we can say that the equivalent resistance $R$ in the circuit is the sum of all the individual resistances in the circuit.
Note:All the resistors in the series do not get a source voltage, therefore, they divide the voltage across them. Also, the amount of energy used by the resistors will be the same as the amount of energy used by a single resistor. This energy is also divided across the resistors depending upon their resistances.
Recently Updated Pages
Choose the option that best corrects the given sentence class 10 english CBSE

Choose the wordphrase which is opposite in meaning class 10 english CBSE

Find the volume m3 in a cube one face of which has class 10 maths CBSE

A solid iron pole consists of a cylinder of height-class-10-maths-CBSE

Which of the following theories has no connection with class 10 physics CBSE

What is the atomic mass of calcium carbonate class 10 chemistry CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




