Question

In the given figure,

(A) $P > {P_0}$
(B) $P < {P_0}$
(C) $P = {P_0}$
(D) $P = 0$

Answer 1

Hint: Pascal’s Law states the pressure is the same on both the arms. Pressure depends on the density and height of the fluid.

Formula Used: The formulae used in the solution are given here.
The pressure due to the weight of a fluid is given by $P = \rho gh$ where $\rho $ is the density of the fluid, $g$ is the acceleration due to gravity and $h$ is the height of the fluid column.

Complete step by step answer
Let us suppose an external force is applied to a surface. The component of the force that is acting perpendicularly to the surface is the normal force. The total normal force applied to the surface divided by the area of the surface is the average pressure on the surface. Pascal's law says that pressure applied to an enclosed fluid will be transmitted without a change in magnitude to every point of the fluid and to the walls of the container. The pressure at any point in the fluid is equal in all directions.
Therefore, at the same level, ${P_{out}} = {P_{in}}$ where ${P_{out}}$ indicates the pressure output and ${P_{in}}$ indicates the pressure input.

We know that the pressure due to the weight of a fluid is given by $P = \rho gh$ where $\rho $ is the density of the fluid, $g$ is the acceleration due to gravity and $h$ is the height of the fluid column.
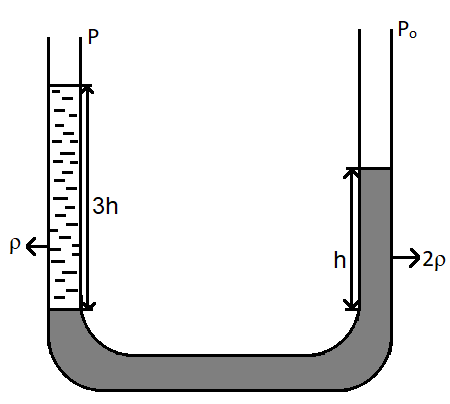
As seen in the figure, a U-shaped tube is filled with fluids. Let us suppose that the arm on the right is arm A and that on the left is arm B.
Thus, it can be written that, pressure on arm A is, $P + \rho g\left( {3h} \right)$, since it is given that the height of the fluid $3h$ and the pressure on arm A is $P$.
The pressure on arm B is ${P_0} + 2\rho gh$, since the density is twice and the pressure on arm B is ${P_0}$.
By Pascal’s Law, the pressure is the same on both the arms.
$P + \rho g\left( {3h} \right) = {P_0} + 2\rho gh$
$P + 3\rho gh - 2\rho gh = {P_0}$
Simplifying the equation,
$ \Rightarrow P + \rho gh = {P_0}$

Thus, it is evident that $P < {P_0}$. Hence, the correct answer is Option B.

Note
Pressure is the force acting perpendicularly on the unit area of the object. Pressure depends upon the factors as follows:-
(1) It depends on the force applied.
(2) Area over in which force acts.
The same force can produce different pressures depending upon the area in which it acts. When the force acts over a large area, the pressure produced is less.
Pressure also depends on the intermolecular forces of attraction present between the molecules of gases confined in a vessel.
Greater the intermolecular forces of attractions lesser the pressure it exerts. This can be explained on the basis of Vander Waals equation.
When there is complete absence of intermolecular forces then that gas exerts more pressure on the walls of the container. Such gas is called Ideal gas. But in nature no gas is found to be ideal.