
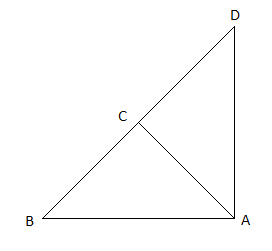
In fig, \[ABD\] is a triangle right angled at \[A\] and \[AC \bot BD\]. Show that,
1. \[A{B^2} = BC.BD\]
2. \[A{C^2} = BC.DC\]
3. \[A{D^2} = BD.DC\]

Answer
553.2k+ views
Hint: At first, using the given condition we will try to find that the triangles are similar.
If the three angles of any triangle are equal to the respective angles of another triangle, then the triangle is called a similar triangle.
Then, by the common side of a similar triangle we can prove the required proof.
Complete step-by-step answer:
It is given that; \[ABD\] is a triangle right angled at \[A\] and \[AC \bot BD\]
We have to show that,
1. \[A{B^2} = BC.BD\]
2. \[A{C^2} = BC.DC\]
3. \[A{D^2} = BD.DC\]
Since, \[AC \bot BD\], \[\Delta ABC\] and \[\Delta BAD\] are right-angle triangles.
So, \[\angle BCA = \angle DAB = {90^ \circ }\]
Again, \[\angle B\] is the common angle of \[\Delta ABC\] and \[\Delta BAD\].
Now, in \[\Delta ABC\] and \[\Delta BAD\], we have,
\[\angle BCA = \angle DAB = {90^ \circ }\]
\[\angle B\] is the common angle
So, by A-A-A condition, \[\Delta ABC\] and \[\Delta BAD\] are similar triangles.
From the common side of similar triangle, we have,
\[\dfrac{{BC}}{{AB}} = \dfrac{{AC}}{{AD}} = \dfrac{{AB}}{{BD}}\]… (1)
And, from the common angle of similar triangle, we have,
\[\angle BAC = \angle BDA\]… (2)
From (1) we get,
\[\dfrac{{BC}}{{AB}} = \dfrac{{AB}}{{BD}}\]
By cross multiplication we get,
\[A{B^2} = BC.BD\]
Again, in \[\Delta ABC\] and \[\Delta CAD\], we have,
\[\angle BCA = \angle DCA\] (each angle is \[{90^ \circ }\])
From (2) we get, \[\angle BAC = \angle BDA\]
So, by A-A-A condition, \[\Delta ABC\] and \[\Delta CAD\] are similar triangles.
From the common side of similar triangle, we have,
\[\dfrac{{BC}}{{AC}} = \dfrac{{AC}}{{CD}} = \dfrac{{AB}}{{AD}}\]
So, \[\dfrac{{BC}}{{AC}} = \dfrac{{AC}}{{CD}}\]
By cross multiplication we get,
\[A{C^2} = BC.DC\]
Since, \[\Delta ABC\] and \[\Delta CAD\] are similar triangles and \[\Delta ABC\] and \[\Delta BAD\] are similar triangles.
So, \[\Delta CAD\] and \[\Delta BAD\] are similar triangles.
From the common side of similar triangle, we have,
\[\dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{CD}} = \dfrac{{BD}}{{AD}}\]
So, \[\dfrac{{AD}}{{CD}} = \dfrac{{BD}}{{AD}}\]
By cross multiplication we get,
\[A{D^2} = BD.DC\]
Hence,
1. \[A{B^2} = BC.BD\]
2. \[A{C^2} = BC.DC\]
3. \[A{D^2} = BD.DC\]
Note: We know that, if the three angles of any triangle are equal to the respective angles of another triangle, then the triangles are called similar triangles. This is known as A-A-A condition.
If all the sides of any triangle are equal to the respective sides of another, then the triangles are called similar triangles. So, the ratio of the respective sides are equal.
If the three angles of any triangle are equal to the respective angles of another triangle, then the triangle is called a similar triangle.
Then, by the common side of a similar triangle we can prove the required proof.
Complete step-by-step answer:
It is given that; \[ABD\] is a triangle right angled at \[A\] and \[AC \bot BD\]
We have to show that,
1. \[A{B^2} = BC.BD\]
2. \[A{C^2} = BC.DC\]
3. \[A{D^2} = BD.DC\]
Since, \[AC \bot BD\], \[\Delta ABC\] and \[\Delta BAD\] are right-angle triangles.
So, \[\angle BCA = \angle DAB = {90^ \circ }\]
Again, \[\angle B\] is the common angle of \[\Delta ABC\] and \[\Delta BAD\].
Now, in \[\Delta ABC\] and \[\Delta BAD\], we have,
\[\angle BCA = \angle DAB = {90^ \circ }\]
\[\angle B\] is the common angle
So, by A-A-A condition, \[\Delta ABC\] and \[\Delta BAD\] are similar triangles.
From the common side of similar triangle, we have,
\[\dfrac{{BC}}{{AB}} = \dfrac{{AC}}{{AD}} = \dfrac{{AB}}{{BD}}\]… (1)
And, from the common angle of similar triangle, we have,
\[\angle BAC = \angle BDA\]… (2)
From (1) we get,
\[\dfrac{{BC}}{{AB}} = \dfrac{{AB}}{{BD}}\]
By cross multiplication we get,
\[A{B^2} = BC.BD\]
Again, in \[\Delta ABC\] and \[\Delta CAD\], we have,
\[\angle BCA = \angle DCA\] (each angle is \[{90^ \circ }\])
From (2) we get, \[\angle BAC = \angle BDA\]
So, by A-A-A condition, \[\Delta ABC\] and \[\Delta CAD\] are similar triangles.
From the common side of similar triangle, we have,
\[\dfrac{{BC}}{{AC}} = \dfrac{{AC}}{{CD}} = \dfrac{{AB}}{{AD}}\]
So, \[\dfrac{{BC}}{{AC}} = \dfrac{{AC}}{{CD}}\]
By cross multiplication we get,
\[A{C^2} = BC.DC\]
Since, \[\Delta ABC\] and \[\Delta CAD\] are similar triangles and \[\Delta ABC\] and \[\Delta BAD\] are similar triangles.
So, \[\Delta CAD\] and \[\Delta BAD\] are similar triangles.
From the common side of similar triangle, we have,
\[\dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{CD}} = \dfrac{{BD}}{{AD}}\]
So, \[\dfrac{{AD}}{{CD}} = \dfrac{{BD}}{{AD}}\]
By cross multiplication we get,
\[A{D^2} = BD.DC\]
Hence,
1. \[A{B^2} = BC.BD\]
2. \[A{C^2} = BC.DC\]
3. \[A{D^2} = BD.DC\]
Note: We know that, if the three angles of any triangle are equal to the respective angles of another triangle, then the triangles are called similar triangles. This is known as A-A-A condition.
If all the sides of any triangle are equal to the respective sides of another, then the triangles are called similar triangles. So, the ratio of the respective sides are equal.
Recently Updated Pages
Draw the graph of y x2 + 2x 3 and hence find the sum class 10 maths CBSE

How many 3 digit numbers can be formed without using class 10 maths CBSE

Choose the correct antonym for the given word HAUGHTY class 10 english CBSE

Find the mean of the first twelve odd natural numbers class 10 maths CBSE

A bicycle is sold for 3000 cash or for Rs 1000 cas-class-10-maths-CBSE

Explain which public facilities are important for Human class 10 social science CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




