Question

In a Fraunhofer diffraction pattern, slit width is $0.2mm$ and screen is at $2m$ away from the lens. If the wavelength of light used is $5000\overset{0}{\mathop{A}}\,$ then the distance between the first minimum on either side of the central maximum will be,
$\begin{align}
  & A{{.10}^{-1}}m \\
 & B{{.10}^{-2}}m \\
 & C.2\times {{10}^{-2}}m \\
 & D.2\times {{10}^{-1}}m \\
\end{align}$

Answer 1

Hint: The distance between the first two minima is to be calculated here. The distance will be the product of the wavelength and the distance between source and the slit divided by the distance between the slits. Don’t forget to multiply the numerator with the order of fringe. By substituting the given values in it, will give the required solution. These all may help you to solve this question.

Formula Used:
\[\beta =\dfrac{n\lambda D}{d}\]
Where \[\beta \] be the distance between the first two minimums, \[\lambda \]be the wavelength used up, \[D\] be the distance between the source and the slit and \[d\] be the distance between the two slits.

Complete step-by-step answer:
First of all let us mention what all are given in the question,
Wavelength of light used is given as,
\[\lambda =5000\overset{0}{\mathop{A}}\,\]
Slit width can be written as,
\[d=0.2mm\]
The distance between the source and the slit can be given as,
\[D=2m\]
As the question is to find the distance between first two minima, the value of \[n\]will be two,
Substituting all the values in the equation will give,
\[\beta =\dfrac{2\times 5000\times {{10}^{-10}}\times 2}{2\times {{10}^{-1}}\times {{10}^{-3}}}\]
Simplifying this will give,
\[\beta =10\times \dfrac{{{10}^{-7}}}{{{10}^{-4}}}={{10}^{-2}}m\]
Therefore the correct answer is option B.

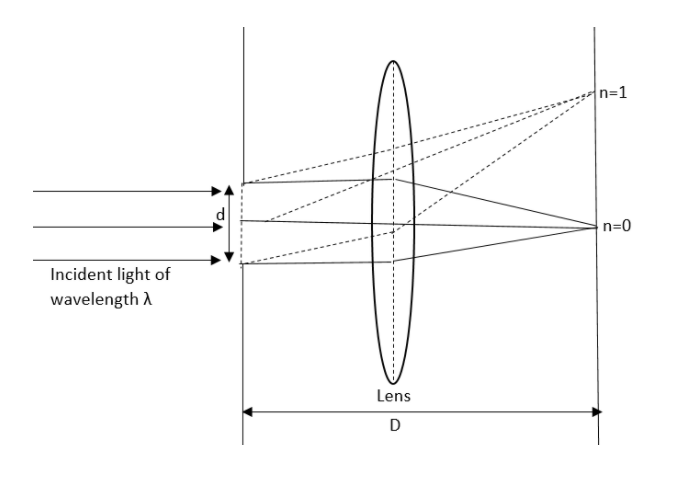
Note: The Fraunhofer diffraction pattern is helpful to picturise the diffraction of waves if the pattern can be observable even at a far distance from the diffracting body. And the difference between Fraunhofer and Fresnel diffraction is that the Fraunhofer diffraction is viewed at the focal plane of a converging lens. But the diffraction pattern created by the Fresnel diffraction is near the object, without using a converging lens.