
If the spinning speed of the earth is increased, then the weight of the body at the equator.
A. does not change
B. doubles
C. decreases
D. increases
Answer
533.4k+ views
Hint: The weight of the body in the absence of rotational motion is mg. This downward force mg is subjected to changes if centripetal force acts too. Velocities of bodies differ if their distances are different from the axis.
Complete step by step answer:
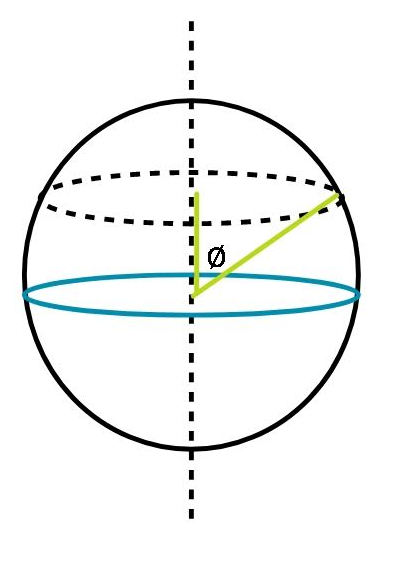
If the earth were not spinning, the weight of the body would have been mg. The earth rotating about its polar axis will make the body undergo a circular motion too. Suppose the object is present at an angle $\phi$ with the polar axis, then, the distance (or radius) from the axis will be $R\sin \phi$ . The centripetal force is given by $mv^2/r$ or $m \omega^2 r$, if the object is at a distance r from the axis. Therefore, we may write:
$mg' = mg - m \omega^2 R\sin \phi$
Canceling the m,
$g' = g - \omega^2 R\sin \phi$.
In the question it has been asked to find what happens to the g when our object is at the equator. So, we are given $\phi = 90^{\circ}$.
This clearly helps us see that the object at the equator will have a g' that is smaller than the actual g. Therefore the correct answer is option (C). The weight of the body decreases at the equator.
So, the correct answer is “Option C”.
Note:
To clear up the formula, consider drawing two perpendicular axes at the point where the object is present. Now, see what angle the centripetal force makes with these axes. mg will be always directed towards the centre of the earth, no matter where it is present and centripetal force points out from the circle that the object makes.
Complete step by step answer:

If the earth were not spinning, the weight of the body would have been mg. The earth rotating about its polar axis will make the body undergo a circular motion too. Suppose the object is present at an angle $\phi$ with the polar axis, then, the distance (or radius) from the axis will be $R\sin \phi$ . The centripetal force is given by $mv^2/r$ or $m \omega^2 r$, if the object is at a distance r from the axis. Therefore, we may write:
$mg' = mg - m \omega^2 R\sin \phi$
Canceling the m,
$g' = g - \omega^2 R\sin \phi$.
In the question it has been asked to find what happens to the g when our object is at the equator. So, we are given $\phi = 90^{\circ}$.
This clearly helps us see that the object at the equator will have a g' that is smaller than the actual g. Therefore the correct answer is option (C). The weight of the body decreases at the equator.
So, the correct answer is “Option C”.
Note:
To clear up the formula, consider drawing two perpendicular axes at the point where the object is present. Now, see what angle the centripetal force makes with these axes. mg will be always directed towards the centre of the earth, no matter where it is present and centripetal force points out from the circle that the object makes.
Recently Updated Pages
Physics and Measurement Mock Test 2025 – Practice Questions & Answers

NCERT Solutions For Class 5 English Marigold - The Little Bully

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.1

NCERT Solutions For Class 11 English Woven Words (Poem) - Ajamil And The Tigers

NCERT Solutions For Class 6 Hindi Durva - Bhaaloo

NCERT Solutions For Class 12 Physics In Hindi - Wave Optics

Trending doubts
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

The process in which gas transform into solid is called class 11 chemistry CBSE

How does Amoeba obtain its food a Endocytosis b Exocytosis class 11 biology ICSE

The string of a kite is 50m long and it makes an angle class 11 maths CBSE

A solution of a substance X is used for white washing class 11 chemistry CBSE




