
If the gravitational potential due to the earth on its surface is assumed to be zero, then gravitational potential at height\[2{{R}_{e}}\]from surface will be
(\[{{R}_{e}}\]:- Radius of the earth; \[g\]:- acceleration due to gravity on earth surface
\[\begin{align}
& A)\dfrac{g{{R}_{e}}}{3} \\
& B)\dfrac{-g{{R}_{e}}}{3} \\
& C)\dfrac{2g{{R}_{e}}}{3} \\
& D)-\dfrac{2g\operatorname{Re}}{3} \\
\end{align}\]
Answer
401.7k+ views
Hint: In this question it is given that at the surface of earth gravitational potential is zero. So first we calculate the change in Gravitational potential energy between earth surface and at some height from earth surface then we apply the relation for gravitational potential and gravitational potential energy.
Complete step-by-step solution:
Let us assume the mass of earth is \[M\] and mass of the body is\[m\].
Since it is given in the question that Gravitational potential on the surface of earth is assumed to be zero.
Let us assume the Gravitational potential on the surface can be represented as\[{{V}_{E}}\].
And also assume that Gravitational potential at height \[2{{R}_{e}}\]from the surface of earth can be represented as\[{{V}_{H}}\].
According to question,
\[{{V}_{E}}=0\].
We have to calculate the value of\[{{V}_{H}}\].
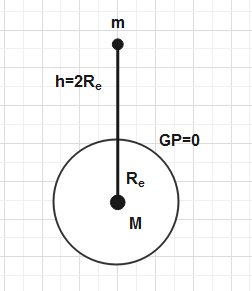
First we calculate the change in potential energy between surfaces of earth to the height\[2{{R}_{e}}\]from the surface of earth.
Let us assume this Change in potential energy can be represented as \[\Delta PE\].
So,
\[\Delta PE=P{{E}_{final}}-P{{E}_{initial}}\]
According to this equation,
Final potential energy can be expressed as : -
\[{{P}_{final}}=\dfrac{-GMm}{3{{R}_{e}}}\]
Initial potential energy can be expressed as :-
\[{{P}_{initial}}=\dfrac{-GMm}{{{R}_{e}}}\]
So , put this value in above equation then change in potential energy can be expressed as
\[\Delta PE=\dfrac{-GMm}{3{{R}_{e}}}-\left( \dfrac{-GMm}{{{R}_{e}}} \right)\]
\[\begin{align}
& \Rightarrow \Delta PE=\dfrac{-GMm}{3{{R}_{e}}}+\dfrac{GMm}{{{R}_{e}}} \\
& \therefore \Delta PE=\dfrac{2GMm}{3{{R}_{e}}}---Equation(1) \\
\end{align}\]
Since we know the relation between change in potential energy and change in gravitational potential can be expressed as: -
\[\Delta V=\dfrac{\Delta PE}{m}\]
Where \[\Delta V\]is representing the change in gravitational potential.
\[\Rightarrow {{V}_{H}}-{{V}_{E}}=\dfrac{\Delta PE}{m}\]
Since potential at surface of earth is zero so this relation can be expressed as: -
\[{{V}_{H}}=\dfrac{\Delta PE}{m}\]
Put the value from equation 1 we get,
\[{{V}_{H}}=\dfrac{2GMm}{3{{R}_{e}}\times m}\]
\[\Rightarrow {{V}_{H}}=\dfrac{2GM}{3{{R}_{e}}}\]
Since we know that the relation between acceleration due to gravity and gravitational constant can be expressed as:-
\[\begin{align}
& \because g=\dfrac{GM}{{{R}_{e}}^{2}} \\
& \therefore GM=g{{R}_{e}}^{2} \\
\end{align}\]
Put it in above equation of gravitational potential we get,
\[{{V}_{H}}=\dfrac{2g{{R}_{e}}}{3}\].
This is the required value of gravitational potential at height \[2{{R}_{e}}\]from the surface of earth.
So, Correct Option is C.
Note: Gravitational force is always attractive in nature. It is also independent of the medium between the particles. It holds well over a wide range of distances. It is found true for interplanetary to inter atomic distances. It is a central force i.e. acts along the line joining the centres of two interacting bodies.
Complete step-by-step solution:
Let us assume the mass of earth is \[M\] and mass of the body is\[m\].
Since it is given in the question that Gravitational potential on the surface of earth is assumed to be zero.
Let us assume the Gravitational potential on the surface can be represented as\[{{V}_{E}}\].
And also assume that Gravitational potential at height \[2{{R}_{e}}\]from the surface of earth can be represented as\[{{V}_{H}}\].
According to question,
\[{{V}_{E}}=0\].
We have to calculate the value of\[{{V}_{H}}\].

First we calculate the change in potential energy between surfaces of earth to the height\[2{{R}_{e}}\]from the surface of earth.
Let us assume this Change in potential energy can be represented as \[\Delta PE\].
So,
\[\Delta PE=P{{E}_{final}}-P{{E}_{initial}}\]
According to this equation,
Final potential energy can be expressed as : -
\[{{P}_{final}}=\dfrac{-GMm}{3{{R}_{e}}}\]
Initial potential energy can be expressed as :-
\[{{P}_{initial}}=\dfrac{-GMm}{{{R}_{e}}}\]
So , put this value in above equation then change in potential energy can be expressed as
\[\Delta PE=\dfrac{-GMm}{3{{R}_{e}}}-\left( \dfrac{-GMm}{{{R}_{e}}} \right)\]
\[\begin{align}
& \Rightarrow \Delta PE=\dfrac{-GMm}{3{{R}_{e}}}+\dfrac{GMm}{{{R}_{e}}} \\
& \therefore \Delta PE=\dfrac{2GMm}{3{{R}_{e}}}---Equation(1) \\
\end{align}\]
Since we know the relation between change in potential energy and change in gravitational potential can be expressed as: -
\[\Delta V=\dfrac{\Delta PE}{m}\]
Where \[\Delta V\]is representing the change in gravitational potential.
\[\Rightarrow {{V}_{H}}-{{V}_{E}}=\dfrac{\Delta PE}{m}\]
Since potential at surface of earth is zero so this relation can be expressed as: -
\[{{V}_{H}}=\dfrac{\Delta PE}{m}\]
Put the value from equation 1 we get,
\[{{V}_{H}}=\dfrac{2GMm}{3{{R}_{e}}\times m}\]
\[\Rightarrow {{V}_{H}}=\dfrac{2GM}{3{{R}_{e}}}\]
Since we know that the relation between acceleration due to gravity and gravitational constant can be expressed as:-
\[\begin{align}
& \because g=\dfrac{GM}{{{R}_{e}}^{2}} \\
& \therefore GM=g{{R}_{e}}^{2} \\
\end{align}\]
Put it in above equation of gravitational potential we get,
\[{{V}_{H}}=\dfrac{2g{{R}_{e}}}{3}\].
This is the required value of gravitational potential at height \[2{{R}_{e}}\]from the surface of earth.
So, Correct Option is C.
Note: Gravitational force is always attractive in nature. It is also independent of the medium between the particles. It holds well over a wide range of distances. It is found true for interplanetary to inter atomic distances. It is a central force i.e. acts along the line joining the centres of two interacting bodies.
Recently Updated Pages
Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
The reservoir of dam is called Govind Sagar A Jayakwadi class 11 social science CBSE

What problem did Carter face when he reached the mummy class 11 english CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

In China rose the flowers are A Zygomorphic epigynous class 11 biology CBSE

What is Environment class 11 chemistry CBSE

Nucleolus is present in which part of the cell class 11 biology CBSE




