
If $\Delta ABC$ is right-angled at B, where $A\left( 5,6,4 \right)$, $B\left( 4,4,1 \right)$, $C\left( 8,2,x \right)$, then find the value of $x$.
Answer
494.1k+ views
Hint: We first use the Pythagoras’ theorem that gives $bas{{e}^{2}}+heigh{{t}^{2}}=hypotenus{{e}^{2}}$. Then we get $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$. We use the distance formula of $d=\sqrt{{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}+{{\left( z-c \right)}^{2}}}$. We find the length of the sides and use them in the formula of $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$. We solve the linear equation to find the value of $x$.
Complete step by step solution:
$\Delta ABC$ is right-angled at B. Therefore, $\angle B={{90}^{\circ }}$ and the side AC is the hypotenuse.
From Pythagoras’ theorem we can say that $bas{{e}^{2}}+heigh{{t}^{2}}=hypotenus{{e}^{2}}$.
Here the rest of the sides AB and BC will be considered as height and base.
We get $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$.
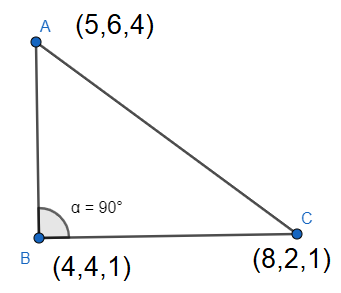
We have been given the coordinates of the vertices.
For two points with coordinates $P\left( x,y,z \right)$, $Q\left( a,b,c \right)$, the distance between them will be
$d=\sqrt{{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}+{{\left( z-c \right)}^{2}}}$.
We find the length of the sides AB, BC, CA.
So, $AB=\sqrt{{{\left( 5-4 \right)}^{2}}+{{\left( 6-4 \right)}^{2}}+{{\left( 4-1 \right)}^{2}}}=\sqrt{14}$
\[AC=\sqrt{{{\left( 5-8 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}+{{\left( 4-x \right)}^{2}}}=\sqrt{{{\left( x-4 \right)}^{2}}+25}\]
\[BC=\sqrt{{{\left( 4-8 \right)}^{2}}+{{\left( 4-2 \right)}^{2}}+{{\left( 1-x \right)}^{2}}}=\sqrt{{{\left( x-1 \right)}^{2}}+20}\]
The equation $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$ gives $14+{{\left( x-1 \right)}^{2}}+20={{\left( x-4 \right)}^{2}}+25$.
We simplify the quadratic to get
$\begin{align}
& 14+{{\left( x-1 \right)}^{2}}+20={{\left( x-4 \right)}^{2}}+25 \\
& \Rightarrow -2x+35=-8x+41 \\
& \Rightarrow 8x-2x=41-35 \\
& \Rightarrow 6x=6 \\
\end{align}$
We now divide both sides with 6 to get $x=\dfrac{6}{6}=1$.
Therefore, the value of $x$ is 1.
Note: We need to be careful about taking the image as 2-D as it is situated in a 3-D plane. The length of the sides will be considered in that way also. The hypotenuse also has to be greater than any other sides and that can be considered as a condition also.
Complete step by step solution:
$\Delta ABC$ is right-angled at B. Therefore, $\angle B={{90}^{\circ }}$ and the side AC is the hypotenuse.
From Pythagoras’ theorem we can say that $bas{{e}^{2}}+heigh{{t}^{2}}=hypotenus{{e}^{2}}$.
Here the rest of the sides AB and BC will be considered as height and base.
We get $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$.

We have been given the coordinates of the vertices.
For two points with coordinates $P\left( x,y,z \right)$, $Q\left( a,b,c \right)$, the distance between them will be
$d=\sqrt{{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}+{{\left( z-c \right)}^{2}}}$.
We find the length of the sides AB, BC, CA.
So, $AB=\sqrt{{{\left( 5-4 \right)}^{2}}+{{\left( 6-4 \right)}^{2}}+{{\left( 4-1 \right)}^{2}}}=\sqrt{14}$
\[AC=\sqrt{{{\left( 5-8 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}+{{\left( 4-x \right)}^{2}}}=\sqrt{{{\left( x-4 \right)}^{2}}+25}\]
\[BC=\sqrt{{{\left( 4-8 \right)}^{2}}+{{\left( 4-2 \right)}^{2}}+{{\left( 1-x \right)}^{2}}}=\sqrt{{{\left( x-1 \right)}^{2}}+20}\]
The equation $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$ gives $14+{{\left( x-1 \right)}^{2}}+20={{\left( x-4 \right)}^{2}}+25$.
We simplify the quadratic to get
$\begin{align}
& 14+{{\left( x-1 \right)}^{2}}+20={{\left( x-4 \right)}^{2}}+25 \\
& \Rightarrow -2x+35=-8x+41 \\
& \Rightarrow 8x-2x=41-35 \\
& \Rightarrow 6x=6 \\
\end{align}$
We now divide both sides with 6 to get $x=\dfrac{6}{6}=1$.
Therefore, the value of $x$ is 1.
Note: We need to be careful about taking the image as 2-D as it is situated in a 3-D plane. The length of the sides will be considered in that way also. The hypotenuse also has to be greater than any other sides and that can be considered as a condition also.
Recently Updated Pages
Explain the double helix structure of DNA with a labeled class 10 biology CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE

Which party gave the slogan Save Democracy in the Lok class 10 social science CBSE

iWhat is Rain Water Harvesting iiWhat are the advantages class 10 social science CBSE

Explain any 5 effects of the Russian Revolution of class 10 social science CBSE

Refractive index of glass with respect to water is class 10 physics CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

The uses of bleaching powder are A It is used bleaching class 10 chemistry CBSE

What is the minimum age for fighting the election in class 10 social science CBSE

The capital of British India was transferred from Calcutta class 10 social science CBSE

Write any two uses of Plaster of Paris class 10 chemistry CBSE




