
If a potential difference across 27-ohm resistor in the circuit shown is 54 volts, then the potential difference across the 4-ohm resistor is:
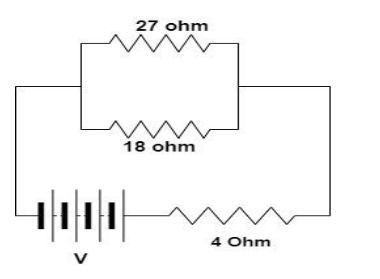
1) 20 volts
2) 10 volts
3) 5 volts
4) 4 volts

Answer
454.5k+ views
Hint:In a parallel circuit the voltage remains same in each of the resistance, so here the voltage across 27 ohm and 18 ohm resistance will be the same. Apply the formula of Ohm’s and find the asked voltage across the 4 ohm resistor.
Complete step by step solution:
Ohm’s law is given as:
V = IR;
Where:
V = voltage;
I = current;
R = Resistance;
Now, we know that to calculate equivalent resistance in parallel the formula is:
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ ;
Put the given value in the above relation:
$\dfrac{1}{R} = \dfrac{1}{{27}} + \dfrac{1}{{18}}$;
Do, the necessary calculation and solve:
$ \Rightarrow \dfrac{1}{R} = \dfrac{9}{{100}}$;
$ \Rightarrow R = \dfrac{{100}}{9}$;
Now, apply Ohm's law:
V = IR ;
Write the above relation in terms of current “I”:
$ \Rightarrow I = \dfrac{V}{R}$ ;
Put the value of voltage and resistance:
$I = \dfrac{{54 \times 9}}{{100}}$;
Do the needed calculation:
$ \Rightarrow I = \dfrac{{486}}{{100}}$;
$ \Rightarrow I = 4.86A$;
Now, we know the current that passes through both the resistances combined, again applying ohm’s law to find the voltage across the 4 ohm resistor.
$V = IR$;
Put the value of voltage and resistance:
$ \Rightarrow V = 4.86 \times 4$;
$ \Rightarrow V = 19.44$;
The voltage across the 4 ohm resistor is:
$ \Rightarrow V \simeq 20Volts$;
Final Answer:Option “1” is correct. Therefore, the potential difference across the 4-ohm resistor is 20 volts.
Note:Here, in case of calculating the equivalent resistance in parallel the formula is $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$, similarly to calculate the resistance in series we have the formula \[R = {R_1} + {R_2}\]. In the case of capacitors just reverse the formula i.e. use the series formula of resistance in the parallel formula for equivalent capacitance and the parallel formula for equivalent resistance in the formula for equivalent capacitance in series.
Complete step by step solution:
Ohm’s law is given as:
V = IR;
Where:
V = voltage;
I = current;
R = Resistance;
Now, we know that to calculate equivalent resistance in parallel the formula is:
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ ;
Put the given value in the above relation:
$\dfrac{1}{R} = \dfrac{1}{{27}} + \dfrac{1}{{18}}$;
Do, the necessary calculation and solve:
$ \Rightarrow \dfrac{1}{R} = \dfrac{9}{{100}}$;
$ \Rightarrow R = \dfrac{{100}}{9}$;
Now, apply Ohm's law:
V = IR ;
Write the above relation in terms of current “I”:
$ \Rightarrow I = \dfrac{V}{R}$ ;
Put the value of voltage and resistance:
$I = \dfrac{{54 \times 9}}{{100}}$;
Do the needed calculation:
$ \Rightarrow I = \dfrac{{486}}{{100}}$;
$ \Rightarrow I = 4.86A$;
Now, we know the current that passes through both the resistances combined, again applying ohm’s law to find the voltage across the 4 ohm resistor.
$V = IR$;
Put the value of voltage and resistance:
$ \Rightarrow V = 4.86 \times 4$;
$ \Rightarrow V = 19.44$;
The voltage across the 4 ohm resistor is:
$ \Rightarrow V \simeq 20Volts$;
Final Answer:Option “1” is correct. Therefore, the potential difference across the 4-ohm resistor is 20 volts.
Note:Here, in case of calculating the equivalent resistance in parallel the formula is $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$, similarly to calculate the resistance in series we have the formula \[R = {R_1} + {R_2}\]. In the case of capacitors just reverse the formula i.e. use the series formula of resistance in the parallel formula for equivalent capacitance and the parallel formula for equivalent resistance in the formula for equivalent capacitance in series.
Recently Updated Pages
Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Explain sex determination in humans with the help of class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers

How do you convert from joules to electron volts class 12 physics CBSE

Differentiate between internal fertilization and external class 12 biology CBSE

On what factors does the internal resistance of a cell class 12 physics CBSE

A 24 volt battery of internal resistance 4 ohm is connected class 12 physics CBSE




