
Given $\theta =\dfrac{19\pi }{6}$, how do you find $\sin \theta $?
Answer
516.3k+ views
Hint: We will use $\sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2}$ to get to the right answer. Also, to simplify the angle we will convert \[\dfrac{19\pi }{6}=6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6}\] and solve it further. Moreover, to know about the presence of an angle is in which quadrant we have to take the help of a graph in which each angle will be $90{}^\circ $ apart.
Complete step-by-step answer:
We will consider the following diagram to solve this question.
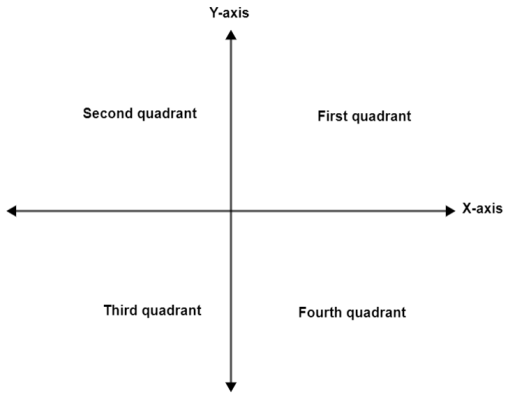
In this question, we can see the four quadrants. Now, we will find out that where the given angle lies in it. For this we need to simplify the angle $\theta =\dfrac{19\pi }{6}$. This can be done as follows,
\[\begin{align}
& \theta =\dfrac{19\pi }{6} \\
& \Rightarrow \theta =\dfrac{18\pi +\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)+\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)}{6}+\dfrac{\pi }{6} \\
& \Rightarrow \theta =6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6}\,...(i) \\
\end{align}\]
Now, in order to find $\sin \left( \theta \right)$, we need to substitute equation (i) in it. Therefore, we get$\sin \left( \theta \right)=\sin \left( 6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6} \right)$. At this point we will move $\dfrac{\pi }{2}$ six times in the above figure. Thus, we get the following new diagram,
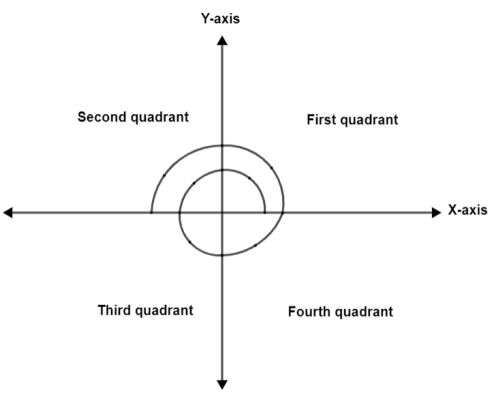
After this we are going to trace $\dfrac{\pi }{6}$ and stop when reached to the third quadrant. Thus, we get
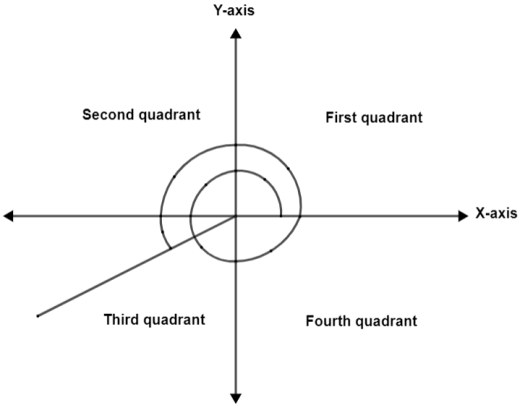
Since, in the third quadrant sine is always negative therefore, we will now have $\sin \left( \theta \right)=-\sin \left( \dfrac{\pi }{6} \right)$. As the value of $\sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2}$ thus, we get $\sin \left( \theta \right)=-\dfrac{1}{2}$.
Hence, the value of $\sin \left( \theta \right)=-\dfrac{1}{2}$.
Note:We could have solve the problem with the following process,
\[\begin{align}
& \theta =\dfrac{19\pi }{6} \\
& \Rightarrow \theta =\dfrac{18\pi +\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)+\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)}{6}+\dfrac{\pi }{6} \\
& \Rightarrow \theta =3\pi +\dfrac{\pi }{6} \\
\end{align}\]
From this method we would have traced $\pi $ instead of $\dfrac{\pi }{2}$ and get to the same answer. But in this case the formula would have used here be \[\sin \left( 3\pi +\dfrac{\pi }{6} \right)=-\sin \left( \dfrac{\pi }{6} \right)\]. Leading towards the right answer must be tricky here as in trigonometry, one small mistake can give wrong angle. This may result into getting no marks at all. The angle of $\pi $ taken here is $180{}^\circ $. This is how we have traced the above diagrams.
Complete step-by-step answer:
We will consider the following diagram to solve this question.

In this question, we can see the four quadrants. Now, we will find out that where the given angle lies in it. For this we need to simplify the angle $\theta =\dfrac{19\pi }{6}$. This can be done as follows,
\[\begin{align}
& \theta =\dfrac{19\pi }{6} \\
& \Rightarrow \theta =\dfrac{18\pi +\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)+\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)}{6}+\dfrac{\pi }{6} \\
& \Rightarrow \theta =6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6}\,...(i) \\
\end{align}\]
Now, in order to find $\sin \left( \theta \right)$, we need to substitute equation (i) in it. Therefore, we get$\sin \left( \theta \right)=\sin \left( 6\left( \dfrac{\pi }{2} \right)+\dfrac{\pi }{6} \right)$. At this point we will move $\dfrac{\pi }{2}$ six times in the above figure. Thus, we get the following new diagram,

After this we are going to trace $\dfrac{\pi }{6}$ and stop when reached to the third quadrant. Thus, we get

Since, in the third quadrant sine is always negative therefore, we will now have $\sin \left( \theta \right)=-\sin \left( \dfrac{\pi }{6} \right)$. As the value of $\sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2}$ thus, we get $\sin \left( \theta \right)=-\dfrac{1}{2}$.
Hence, the value of $\sin \left( \theta \right)=-\dfrac{1}{2}$.
Note:We could have solve the problem with the following process,
\[\begin{align}
& \theta =\dfrac{19\pi }{6} \\
& \Rightarrow \theta =\dfrac{18\pi +\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)+\pi }{6} \\
& \Rightarrow \theta =\dfrac{6\left( 3\pi \right)}{6}+\dfrac{\pi }{6} \\
& \Rightarrow \theta =3\pi +\dfrac{\pi }{6} \\
\end{align}\]
From this method we would have traced $\pi $ instead of $\dfrac{\pi }{2}$ and get to the same answer. But in this case the formula would have used here be \[\sin \left( 3\pi +\dfrac{\pi }{6} \right)=-\sin \left( \dfrac{\pi }{6} \right)\]. Leading towards the right answer must be tricky here as in trigonometry, one small mistake can give wrong angle. This may result into getting no marks at all. The angle of $\pi $ taken here is $180{}^\circ $. This is how we have traced the above diagrams.
Recently Updated Pages
Explain the double helix structure of DNA with a labeled class 10 biology CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE

Which party gave the slogan Save Democracy in the Lok class 10 social science CBSE

iWhat is Rain Water Harvesting iiWhat are the advantages class 10 social science CBSE

Explain any 5 effects of the Russian Revolution of class 10 social science CBSE

Refractive index of glass with respect to water is class 10 physics CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

The uses of bleaching powder are A It is used bleaching class 10 chemistry CBSE

Write any two uses of Plaster of Paris class 10 chemistry CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Discuss the main reasons for poverty in India




