
How to find two missing sides of a right triangle with a right angle and a \[50\] degree angle if the hypotenuse is \[2\sqrt 2 {\text{ units}}\].
Answer
483.6k+ views
Hint:We are given the values of hypotenuse and one angle of a right angled triangle and asked to find the value of the other two sides that are base and perpendicular. For this, you will need to recall the formulas of sine and cosine functions in terms of sides of a right angled triangle.
Use those formulas and find the values of the other two sides of the right angled triangle.
Complete step by step solution:
Given, one angle of a right angled triangle is \[{50^{\text{o}}}\] and the hypotenuse is \[2\sqrt 2 {\text{ units}}\].
We are asked to find the other two sides.
Let the right angled triangle be ABC with \[\theta = {50^{\text{o}}}\] and the hypotenuse is \[2\sqrt
2 {\text{ units}}\]..
We draw the right angled triangle.
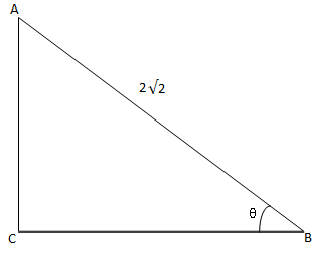
In the figure, the hypotenuse is \[AB = 2\sqrt 2 {\text{ units}}\], base is \[BC\] and perpendicular is
\[AC\].
We know sine and cosine of an angle can be written in terms of perpendicular, base and hypotenuse of a right angled triangle.
We can write sine function as,
\[\sin \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}\] (i)
We can write cosine function as,
\[\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}\] (ii)
Putting the values of \[\theta \], perpendicular and hypotenuse in equation (i) we get,
\[\sin {50^{\text{o}}} = \dfrac{{AC}}{{2\sqrt 2 }}\]
\[ \Rightarrow AC = 2\sqrt 2 \sin {50^{\text{o}}}\]
\[ \Rightarrow AC = 2\sqrt 2 \times 0.766\]
\[ \Rightarrow AC = 2.16\;{\text{units}}\]
Putting the values of \[\theta \], base and hypotenuse in equation (i) we get,
\[\cos {50^{\text{o}}} = \dfrac{{BC}}{{2\sqrt 2 }}\]
\[ \Rightarrow BC = 2\sqrt 2 \cos {50^{\text{o}}}\]
\[ \Rightarrow BC = 2\sqrt 2 \times 0.642\]
\[ \Rightarrow BC = 1.81{\text{ units}}\]
The values of other two sides of the right angled triangle are \[{\text{2}}{\text{.16 units}}\] and \[1.81{\text{ units}}\]
Note: There is an important theorem related to the right angled triangle that is the Pythagoras theorem. According to Pythagoras theorem, the square of hypotenuse is equal to the sum of square of base and square of perpendicular of the triangle. Here, we are asked to find two sides of the right angled triangle but if we are given two sides and asked to find the third side of the right angled triangle then we can use Pythagoras theorem to find the side.
Use those formulas and find the values of the other two sides of the right angled triangle.
Complete step by step solution:
Given, one angle of a right angled triangle is \[{50^{\text{o}}}\] and the hypotenuse is \[2\sqrt 2 {\text{ units}}\].
We are asked to find the other two sides.
Let the right angled triangle be ABC with \[\theta = {50^{\text{o}}}\] and the hypotenuse is \[2\sqrt
2 {\text{ units}}\]..
We draw the right angled triangle.

In the figure, the hypotenuse is \[AB = 2\sqrt 2 {\text{ units}}\], base is \[BC\] and perpendicular is
\[AC\].
We know sine and cosine of an angle can be written in terms of perpendicular, base and hypotenuse of a right angled triangle.
We can write sine function as,
\[\sin \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}\] (i)
We can write cosine function as,
\[\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}\] (ii)
Putting the values of \[\theta \], perpendicular and hypotenuse in equation (i) we get,
\[\sin {50^{\text{o}}} = \dfrac{{AC}}{{2\sqrt 2 }}\]
\[ \Rightarrow AC = 2\sqrt 2 \sin {50^{\text{o}}}\]
\[ \Rightarrow AC = 2\sqrt 2 \times 0.766\]
\[ \Rightarrow AC = 2.16\;{\text{units}}\]
Putting the values of \[\theta \], base and hypotenuse in equation (i) we get,
\[\cos {50^{\text{o}}} = \dfrac{{BC}}{{2\sqrt 2 }}\]
\[ \Rightarrow BC = 2\sqrt 2 \cos {50^{\text{o}}}\]
\[ \Rightarrow BC = 2\sqrt 2 \times 0.642\]
\[ \Rightarrow BC = 1.81{\text{ units}}\]
The values of other two sides of the right angled triangle are \[{\text{2}}{\text{.16 units}}\] and \[1.81{\text{ units}}\]
Note: There is an important theorem related to the right angled triangle that is the Pythagoras theorem. According to Pythagoras theorem, the square of hypotenuse is equal to the sum of square of base and square of perpendicular of the triangle. Here, we are asked to find two sides of the right angled triangle but if we are given two sides and asked to find the third side of the right angled triangle then we can use Pythagoras theorem to find the side.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

Whales are warmblooded animals which live in cold seas class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

Explain zero factorial class 11 maths CBSE




