
What is banking of road? Why is banking necessary for a curved road?
Answer
468.1k+ views
Hint: The process of raising the outer edge of the curved road above the inner edge is known as banking of roads by doing so the vehicle can go round the curved track at a reasonable speed without skidding.
Complete step by step answer:
When a vehicle goes round a curved road, it requires some centripetal force. While rounding the curve, the wheels of the vehicle have a tendency to leave the curved path and regain its original path i.e., straight line. Now the force of friction between wheels and the roads opposes this tendency. This force of friction therefore, acts towards the centre of the circular track and provides the necessary centripetal force (shown by the diagram).
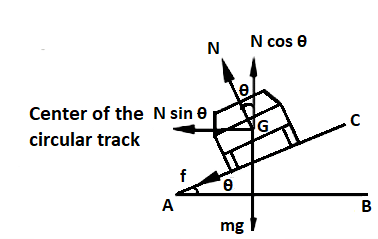
On observing this situation, we find that the maximum permissible velocity with which a vehicle can go round a level curved road depends on ‘μ’ i.e., the coefficient of friction between tyres and road.
The value of ‘μ’ decreases when the road is wet or extra smooth or tyres of the vehicle are worn out. So, we can say that the force of friction is not a reliable source for providing the required centripetal force to the vehicle.
Now, if we made any attempt to run it at a greater speed, the vehicle is likely to skid and go out of track. In order that the vehicle can go round the curved track at a reasonable speed without skidding, the sufficient centripetal force is managed for it by raising the outer edge of the track a little above the inner edge. This process is called the banking of the circular track or banking of roads.
Note: Students should understand the concept of banking of roads thoroughly because by doing so they will become more skilled in solving problems of mechanics. Students should keep in mind that the concept of banking of the road can be better understood with the previous knowledge of centripetal force and frictional force.
Complete step by step answer:
When a vehicle goes round a curved road, it requires some centripetal force. While rounding the curve, the wheels of the vehicle have a tendency to leave the curved path and regain its original path i.e., straight line. Now the force of friction between wheels and the roads opposes this tendency. This force of friction therefore, acts towards the centre of the circular track and provides the necessary centripetal force (shown by the diagram).

On observing this situation, we find that the maximum permissible velocity with which a vehicle can go round a level curved road depends on ‘μ’ i.e., the coefficient of friction between tyres and road.
The value of ‘μ’ decreases when the road is wet or extra smooth or tyres of the vehicle are worn out. So, we can say that the force of friction is not a reliable source for providing the required centripetal force to the vehicle.
Now, if we made any attempt to run it at a greater speed, the vehicle is likely to skid and go out of track. In order that the vehicle can go round the curved track at a reasonable speed without skidding, the sufficient centripetal force is managed for it by raising the outer edge of the track a little above the inner edge. This process is called the banking of the circular track or banking of roads.
Note: Students should understand the concept of banking of roads thoroughly because by doing so they will become more skilled in solving problems of mechanics. Students should keep in mind that the concept of banking of the road can be better understood with the previous knowledge of centripetal force and frictional force.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




