
A wheel has three spokes and in a uniform magnetic field perpendicular to its plane, with the axis of rotation of the wheel parallel to the magnetic field. When the wheel rotates with a uniform angular velocity $\omega $ , the emf induced between the center and rim of the wheel is $e$ , if another wheel having same radius but with six spokes is kept in the same field and rotated with a uniform angular velocity $\dfrac{\omega }{2}$ . The emf induced between the center and the rim will be :
A)$e$
B)$\dfrac{e}{2}$
C)$2e$
D)$\dfrac{e}{4}$
Answer
478.8k+ views
Hint: Spoke is one of some number of rods radiating from the center of a wheel. Spoke are connecting rods between bicycle hub and the rim the purpose of the spoke is to transfer the load between the hub and rim, spokes are made of steel and that steel may be a stainless steel or high carbon steel.
Complete step-by-step solution:
Faraday's law of induction which predicts how a magnetic field interacts with electric field to induce an electromotive force this phenomenon is known as electrometric induction. Electromagnetic induction principle is used in transformers, generators and many other devices.
Faraday’s first laws of electromagnetic induction states that when a conductor is rotating in a magnetic field an emf is induced in a circuit.
Faraday's second of electromagnetic induction states that the rate of change of flux linkages is equal to the induced emf
$e=-N\dfrac{dQ}{dt}Volts$
Negative sign represents the direction of the induced current and will be in the opposite direction.
Emf induced in a rotating conductor in uniform magnetic field
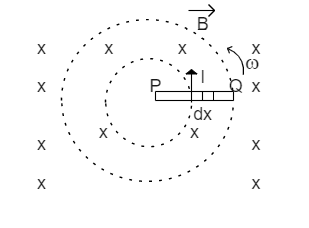
From the diagram you can see that uniform magnetic field$(\overrightarrow{B)}$ existing in opposite direction and rod PQ is rotating with an angular speed $\omega $ and we consider an element $dx$ with velocity $v$
Motional emf induced in element $dx$ is
$de=Bvdx$
Total emf induced across P and Q is
${{e}_{PQ}}=\int{de=\int\limits_{0}^{l}{B(x\omega )dx}}$
${{e}_{PQ}}=B\omega \left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{l}$
${{e}_{PQ}}=\dfrac{1}{2}B\omega {{l}^{2}}$
The emf induced between the center and the rim will be
$e=\dfrac{1}{2}B{{R}^{2}}\omega $
$\therefore $ Emf induced is independent upon the number of spokes
Induced emf$(e)$ is directly proportional to angular velocity($\omega $
$e\propto w$
If the angular velocity is$\dfrac{\omega }{2}$ then the emf induced will be$\dfrac{e}{2}$
So option B is the correct answer.
Note: Student the emf induced between the center and the rim can be obtained by faraday's laws and also by motional emf. Emf induced is independent upon the number of spokes. The number of spokes may be 3 or else 6 and it depends upon the velocity .Lighter wheel performances better than the stronger wheel.
Complete step-by-step solution:
Faraday's law of induction which predicts how a magnetic field interacts with electric field to induce an electromotive force this phenomenon is known as electrometric induction. Electromagnetic induction principle is used in transformers, generators and many other devices.
Faraday’s first laws of electromagnetic induction states that when a conductor is rotating in a magnetic field an emf is induced in a circuit.
Faraday's second of electromagnetic induction states that the rate of change of flux linkages is equal to the induced emf
$e=-N\dfrac{dQ}{dt}Volts$
Negative sign represents the direction of the induced current and will be in the opposite direction.
Emf induced in a rotating conductor in uniform magnetic field

From the diagram you can see that uniform magnetic field$(\overrightarrow{B)}$ existing in opposite direction and rod PQ is rotating with an angular speed $\omega $ and we consider an element $dx$ with velocity $v$
Motional emf induced in element $dx$ is
$de=Bvdx$
Total emf induced across P and Q is
${{e}_{PQ}}=\int{de=\int\limits_{0}^{l}{B(x\omega )dx}}$
${{e}_{PQ}}=B\omega \left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{l}$
${{e}_{PQ}}=\dfrac{1}{2}B\omega {{l}^{2}}$
The emf induced between the center and the rim will be
$e=\dfrac{1}{2}B{{R}^{2}}\omega $
$\therefore $ Emf induced is independent upon the number of spokes
Induced emf$(e)$ is directly proportional to angular velocity($\omega $
$e\propto w$
If the angular velocity is$\dfrac{\omega }{2}$ then the emf induced will be$\dfrac{e}{2}$
So option B is the correct answer.
Note: Student the emf induced between the center and the rim can be obtained by faraday's laws and also by motional emf. Emf induced is independent upon the number of spokes. The number of spokes may be 3 or else 6 and it depends upon the velocity .Lighter wheel performances better than the stronger wheel.
Recently Updated Pages
Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




