
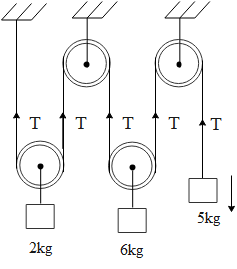
A system of pulley and block is arranged as shown in the figure. Find the acceleration of the block 5kg, 2kg, 6kg.

Answer
580.5k+ views
Hint: In the above diagram we can see that the block of 5kg is moving downwards. Therefore from that we can imply that the other two blocks will move up as the string across them will get reduced. For the above pulley problem we would use the equation for tension in constrained motion. Further we will determine the net force acting on each of the blocks and then again substituting for acceleration in the equation of tension of the individual blocks will enable us to estimate their respective acceleration.
Formula used:
$\sum{Ta=0}$
${{F}_{NET}}=ma$
Complete answer:
In the above diagram let us say the block of 5kg, 6kg and 2kg respectively move with acceleration of ${{a}_{1}}\text{, }{{a}_{2}}\text{ }and\text{ }{{a}_{3}}$ respectively. Hence we can write the net force on the block of 5kg as difference of force due to gravity and the tension in the rope. Mathematically this can be written as,
$\begin{align}
& {{F}_{NET}}=mg-T \\
& \Rightarrow 5{{a}_{1}}=5g-T...(1) \\
\end{align}$
Similarly for a block of 6kg and 2kg we can write, the net force on them as,
$\begin{align}
& \text{For 6kg,} \\
& {{F}_{NET}}=2T-mg \\
& \Rightarrow 6{{a}_{2}}=2T-6g...(2) \\
& \text{For 2kg,} \\
& {{F}_{NET}}=2T-mg \\
& \Rightarrow 2{{a}_{3}}=2T-2g...(3) \\
\end{align}$
Now as per the equation of constrained motion, it tells us that the sum of the total tension in the rope times the acceleration of each of the block is zero .i.e. mathematically can be written as,
$\sum{Ta=0}$ where T is the tension in the rope across the individual masses having different acceleration a.
Hence using this above equation in the above figure we get,
$\begin{align}
& \sum{Ta=0} \\
& \Rightarrow 2T(-{{a}_{3}})+2T(-{{a}_{2}})+T{{a}_{1}}=0 \\
& \Rightarrow 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0...(4) \\
\end{align}$
Since the tension in the string is the same, from equation 1 and, 2 and 3 and 3 and 1 we get,
From 1 and 2,
$\begin{align}
& T=5g-5{{a}_{1}}=3{{a}_{2}}+3g \\
& \Rightarrow 5{{a}_{1}}+3{{a}_{2}}=2g \\
\end{align}$
From 2 and 3,
$\begin{align}
& T=3{{a}_{2}}+3g=g+{{a}_{3}} \\
& \Rightarrow {{a}_{3}}-3{{a}_{2}}=2g \\
\end{align}$
From 3 and 1,
$\begin{align}
& T=5g-5{{a}_{1}}={{a}_{3}}+g \\
& \Rightarrow {{a}_{3}}+5{{a}_{1}}=4g \\
\end{align}$
Now let us substitute equation 4 totally in terms of ${{a}_{1}}$,
$\begin{align}
& 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0 \\
& \Rightarrow 2(4g-5{{a}_{1}})+2(\dfrac{2g-5{{a}_{1}}}{3})-{{a}_{1}}=0 \\
& \Rightarrow 8g-10{{a}_{1}}+\dfrac{4g}{3}-\dfrac{10{{a}_{1}}}{3}-{{a}_{1}}=0 \\
& \Rightarrow -10{{a}_{1}}-\dfrac{10{{a}_{1}}}{3}-{{a}_{1}}=-\dfrac{4g}{3}-8g \\
& \Rightarrow -\dfrac{43{{a}_{1}}}{3}=-\dfrac{28g}{3} \\
& \Rightarrow {{a}_{1}}=\dfrac{28}{43}g\text{, }\because \text{ }g=10m{{s}^{-2}} \\
& \Rightarrow {{a}_{1}}=6.5m{{s}^{-2}} \\
\end{align}$
Now let us determine the acceleration using a similar procedure of mass 6kg.
$\begin{align}
& 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0 \\
& \Rightarrow 2(2g+3{{a}_{2}})+2{{a}_{2}}-(\dfrac{2g-3{{a}_{2}}}{5})=0 \\
& \Rightarrow 4g+6{{a}_{2}}+2{{a}_{2}}-\dfrac{2g}{5}+\dfrac{3{{a}_{2}}}{5}=0 \\
& \Rightarrow 6{{a}_{2}}+2{{a}_{2}}+\dfrac{3{{a}_{2}}}{5}=-4g+\dfrac{2g}{5} \\
& \Rightarrow -\dfrac{43{{a}_{2}}}{5}=-\dfrac{18g}{5} \\
& \Rightarrow {{a}_{2}}=-\dfrac{18}{43}g\text{, }\because \text{ }g=10m{{s}^{-2}} \\
& \Rightarrow {{a}_{2}}=-4.2m{{s}^{-2}} \\
\end{align}$
Now let us determine the acceleration using a similar procedure of mass 2kg.
$\begin{align}
& 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0 \\
& \Rightarrow 2{{a}_{3}}+2(\dfrac{{{a}_{3}}-2g}{3})-(\dfrac{4g-{{a}_{3}}}{5})=0 \\
& \Rightarrow 2{{a}_{3}}+\dfrac{2{{a}_{3}}}{3}-\dfrac{4g}{3}-\dfrac{4g}{5}+\dfrac{{{a}_{3}}}{5}=0 \\
& \Rightarrow 2{{a}_{3}}+\dfrac{2{{a}_{3}}}{3}+\dfrac{{{a}_{3}}}{5}=\dfrac{4g}{3}+\dfrac{4g}{5} \\
& \Rightarrow -\dfrac{43{{a}_{3}}}{15}=\dfrac{32g}{15} \\
& \Rightarrow {{a}_{3}}=\dfrac{32}{43}g\text{, }\because \text{ }g=10m{{s}^{-2}} \\
& \Rightarrow {{a}_{3}}=7.4m{{s}^{-2}} \\
\end{align}$
Hence the acceleration of the above blocks i.e. 5kg, 6kg and 2kg are $6.5m{{s}^{-2}}\text{, 4}\text{.2}m{{s}^{-2}}and7.4m{{s}^{-2}}$ respectively.
Note:
It is to be noted that the pulley as well as the string is considered to be massless. Hence We have considered the tension to be the same throughout the string. It is also to be noted that we can take any convention of the masses moving in a particular direction but the final answer would remain the same.
Formula used:
$\sum{Ta=0}$
${{F}_{NET}}=ma$
Complete answer:
In the above diagram let us say the block of 5kg, 6kg and 2kg respectively move with acceleration of ${{a}_{1}}\text{, }{{a}_{2}}\text{ }and\text{ }{{a}_{3}}$ respectively. Hence we can write the net force on the block of 5kg as difference of force due to gravity and the tension in the rope. Mathematically this can be written as,
$\begin{align}
& {{F}_{NET}}=mg-T \\
& \Rightarrow 5{{a}_{1}}=5g-T...(1) \\
\end{align}$
Similarly for a block of 6kg and 2kg we can write, the net force on them as,
$\begin{align}
& \text{For 6kg,} \\
& {{F}_{NET}}=2T-mg \\
& \Rightarrow 6{{a}_{2}}=2T-6g...(2) \\
& \text{For 2kg,} \\
& {{F}_{NET}}=2T-mg \\
& \Rightarrow 2{{a}_{3}}=2T-2g...(3) \\
\end{align}$
Now as per the equation of constrained motion, it tells us that the sum of the total tension in the rope times the acceleration of each of the block is zero .i.e. mathematically can be written as,
$\sum{Ta=0}$ where T is the tension in the rope across the individual masses having different acceleration a.
Hence using this above equation in the above figure we get,
$\begin{align}
& \sum{Ta=0} \\
& \Rightarrow 2T(-{{a}_{3}})+2T(-{{a}_{2}})+T{{a}_{1}}=0 \\
& \Rightarrow 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0...(4) \\
\end{align}$
Since the tension in the string is the same, from equation 1 and, 2 and 3 and 3 and 1 we get,
From 1 and 2,
$\begin{align}
& T=5g-5{{a}_{1}}=3{{a}_{2}}+3g \\
& \Rightarrow 5{{a}_{1}}+3{{a}_{2}}=2g \\
\end{align}$
From 2 and 3,
$\begin{align}
& T=3{{a}_{2}}+3g=g+{{a}_{3}} \\
& \Rightarrow {{a}_{3}}-3{{a}_{2}}=2g \\
\end{align}$
From 3 and 1,
$\begin{align}
& T=5g-5{{a}_{1}}={{a}_{3}}+g \\
& \Rightarrow {{a}_{3}}+5{{a}_{1}}=4g \\
\end{align}$
Now let us substitute equation 4 totally in terms of ${{a}_{1}}$,
$\begin{align}
& 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0 \\
& \Rightarrow 2(4g-5{{a}_{1}})+2(\dfrac{2g-5{{a}_{1}}}{3})-{{a}_{1}}=0 \\
& \Rightarrow 8g-10{{a}_{1}}+\dfrac{4g}{3}-\dfrac{10{{a}_{1}}}{3}-{{a}_{1}}=0 \\
& \Rightarrow -10{{a}_{1}}-\dfrac{10{{a}_{1}}}{3}-{{a}_{1}}=-\dfrac{4g}{3}-8g \\
& \Rightarrow -\dfrac{43{{a}_{1}}}{3}=-\dfrac{28g}{3} \\
& \Rightarrow {{a}_{1}}=\dfrac{28}{43}g\text{, }\because \text{ }g=10m{{s}^{-2}} \\
& \Rightarrow {{a}_{1}}=6.5m{{s}^{-2}} \\
\end{align}$
Now let us determine the acceleration using a similar procedure of mass 6kg.
$\begin{align}
& 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0 \\
& \Rightarrow 2(2g+3{{a}_{2}})+2{{a}_{2}}-(\dfrac{2g-3{{a}_{2}}}{5})=0 \\
& \Rightarrow 4g+6{{a}_{2}}+2{{a}_{2}}-\dfrac{2g}{5}+\dfrac{3{{a}_{2}}}{5}=0 \\
& \Rightarrow 6{{a}_{2}}+2{{a}_{2}}+\dfrac{3{{a}_{2}}}{5}=-4g+\dfrac{2g}{5} \\
& \Rightarrow -\dfrac{43{{a}_{2}}}{5}=-\dfrac{18g}{5} \\
& \Rightarrow {{a}_{2}}=-\dfrac{18}{43}g\text{, }\because \text{ }g=10m{{s}^{-2}} \\
& \Rightarrow {{a}_{2}}=-4.2m{{s}^{-2}} \\
\end{align}$
Now let us determine the acceleration using a similar procedure of mass 2kg.
$\begin{align}
& 2{{a}_{3}}+2{{a}_{2}}-{{a}_{1}}=0 \\
& \Rightarrow 2{{a}_{3}}+2(\dfrac{{{a}_{3}}-2g}{3})-(\dfrac{4g-{{a}_{3}}}{5})=0 \\
& \Rightarrow 2{{a}_{3}}+\dfrac{2{{a}_{3}}}{3}-\dfrac{4g}{3}-\dfrac{4g}{5}+\dfrac{{{a}_{3}}}{5}=0 \\
& \Rightarrow 2{{a}_{3}}+\dfrac{2{{a}_{3}}}{3}+\dfrac{{{a}_{3}}}{5}=\dfrac{4g}{3}+\dfrac{4g}{5} \\
& \Rightarrow -\dfrac{43{{a}_{3}}}{15}=\dfrac{32g}{15} \\
& \Rightarrow {{a}_{3}}=\dfrac{32}{43}g\text{, }\because \text{ }g=10m{{s}^{-2}} \\
& \Rightarrow {{a}_{3}}=7.4m{{s}^{-2}} \\
\end{align}$
Hence the acceleration of the above blocks i.e. 5kg, 6kg and 2kg are $6.5m{{s}^{-2}}\text{, 4}\text{.2}m{{s}^{-2}}and7.4m{{s}^{-2}}$ respectively.
Note:
It is to be noted that the pulley as well as the string is considered to be massless. Hence We have considered the tension to be the same throughout the string. It is also to be noted that we can take any convention of the masses moving in a particular direction but the final answer would remain the same.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




