Question

A solid disk is rolling without slipping on a level surface at a constant speed of \[2.0m{{s}^{-1}}\].How far can it roll up a \[{{30}^{0}}\]ramp before it stops?(Take \[g=9.8m{{s}^{-2}}\])

Answer 1

Hint: Since, a solid disc is rolling without slipping so we considered it as a pure rolling and for this linear velocity of centre of mass is equal to angular velocity of disc. Since this is pure rolling motion so no work is done due to friction then only conservation of energy is applied only conservative forces are acting.

Complete answer:
A solid disc is moving on a level surface at constant speed of \[2.0m{{s}^{-1}}\].This solid disc is moving on a ramp at angle of \[{{30}^{0}}\].We have to calculate how much distance the solid disc will move till it stops.
Since it is given in the question that the disc is rolling without slipping which means pure rolling takes place.
Let us assume disc is moving linearly so velocity of centre of mass is v and disc is rolling with angular velocity\[\omega \].
Let us assume the radius of the disc is R.
For pure rolling this below equation is satisfied,
\[v=R\omega \](Equation 1)
And for pure rolling velocity of point of Contact which is represented by C is also 0.
When this disc rolls on an inclined plane then a number of forces are acting on it. These forces are represented as: -
1. Friction force f.
2. Weight of disc W. (Acting Vertically downward)
3. Normal reaction to surface N. (Acting perpendicular to inclined plane)

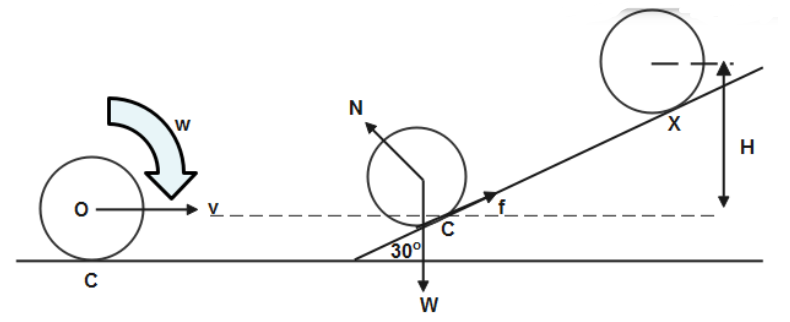
As it is pure rolling motion so velocity at point of contact C is 0 throughout the motion.
As this frictional force is acting at point of contact C and velocity at point of contact C is zero so no work is done due to frictional force.
So work done on this system is due to conservative forces which mean only the forces due to gravity.
Now this disc will stop on an inclined plane after reaching the top most point at X where linear velocity V becomes zero as it is a pure rolling motion so from equation 1 angular velocity\[\omega =0\].
Let us assume the vertical height of the centre of mass solid disc is H from the initial height of centre of mass.
According to conservation of energy, total mechanical energy of the system is always constant.
Initial Kinetic Energy of rolling disc changes into potential energy after reaching highest point X
 Initial Rotational kinetic energy + Linear Kinetic energy = Final Potential Energy
\[\dfrac{1}{2}I{{\omega }^{2}}+\dfrac{1}{2}m{{v}^{2}}=mgH\]
Put the value of \[\omega \] from equation 1, we get
\[\Rightarrow I{{(\dfrac{v}{R})}^{2}}+m{{v}^{2}}=2mgH\]
The moment of inertia of the disc is represented by\[I=\dfrac{m{{R}^{2}}}{2}\].
Put the value in above equation, we get
\[\Rightarrow \dfrac{m{{R}^{2}}}{2}\times \dfrac{{{v}^{2}}}{{{R}^{2}}}+m{{v}^{2}}=2mgH\]
On Simplifying, we get
\[\Rightarrow \]\[\dfrac{3{{v}^{2}}}{2}=2gH\]
\[\therefore H=\dfrac{3{{v}^{2}}}{4g}\]
Put the value of velocity from the given question.
\[\therefore H=\dfrac{3\times 4}{4\times 9.8}\]
\[\therefore H=\dfrac{3}{9.8}m\]
We have to calculate the inclined distance CX.
In triangle CDX,
\[\Rightarrow \]\[Sin{{30}^{0}}=\dfrac{H}{CX}\]
\[\Rightarrow \]\[CX=\dfrac{H}{Sin{{30}^{0}}}\]
\[\Rightarrow CX=\dfrac{3\times 2}{9.8}=\dfrac{6}{9.8}\]
\[\therefore CX=0.612m\]
So solid disks roll upto distance of 0.612m on an inclined plane.

Note:
Purely rotational motion or rolling without slipping occurs if every particle in the body moves in a circle about a single line or along the center of mass. This line is called the axis of rotation. For pure rolling motion linear velocity is equal to angular velocity. During pure rolling work done due fractional forces is always zero.