
A deer wants to save her life from a lion. The lion follows a path whose equation is ${x^2} + {y^2} = 16$. For saving life, the deer moves on a path whose equation is (are):
A. ${x^2} + {y^2} = 4$
B. ${x^2} + {y^2} = 16$
C. ${x^2} + {y^2} - 64 = 0$
D. Both (a) and (c) are correct.
Answer
554.7k+ views
Hint: We are given an equation of the path which is followed by a lion. And the equation resembles a circle equation and the right hand side value of the equation is the square of the path’s radius. So deer must not follow the path which is followed by the lion to save her life. So find the equations with different path radius from the lion’s path radius.
Complete step by step answer:
We are given that a deer wants to save her life from a lion and the lion follows a path whose equation is ${x^2} + {y^2} = 16$.
We have to find the equation(s) of the path to be followed by deer such that she can save her life.
General equation of a circle is ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, where r is the radius of the circle and (h, k) are the coordinates of its centre point.
So when we compare the given path equation followed by lion with above equation we get that,
$
\left( {h,k} \right) = \left( {0,0} \right) \\
\Rightarrow {r^2} = 16 \\
\Rightarrow r = 4 \\
$
The centre is at origin and the radius of the path is 4 units.
So in the given options,
The first equation is ${x^2} + {y^2} = 4$, here the centre is at the origin and the radius is ${r^2} = 4 \to r = 2$ units.
The second equation is the same as the path equation followed by the lion.
The third equation is ${x^2} + {y^2} - 64 = 0 \to {x^2} + {y^2} = 64$, here also the centre is at the origin and the radius is ${r^2} = 64 \to r = 8$ units.
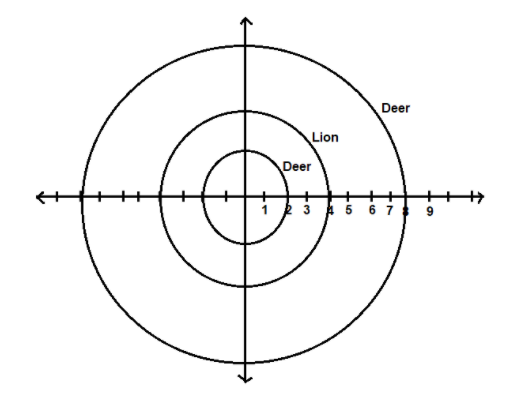
So the first and the third path equations have different radii from the lion’s path radius and deer can save her life by following these paths.
So Option A and Option C are correct.
Hence, the correct option is Option D, both (a) and (c) are correct.
Note: Do not forget to write units of a measurement. If no units like metres, centimeters are given in the question then just write “units” after its value. And radius is always positive and will never be negative whereas the coordinates of the centre can be negative values.
Complete step by step answer:
We are given that a deer wants to save her life from a lion and the lion follows a path whose equation is ${x^2} + {y^2} = 16$.
We have to find the equation(s) of the path to be followed by deer such that she can save her life.
General equation of a circle is ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, where r is the radius of the circle and (h, k) are the coordinates of its centre point.
So when we compare the given path equation followed by lion with above equation we get that,
$
\left( {h,k} \right) = \left( {0,0} \right) \\
\Rightarrow {r^2} = 16 \\
\Rightarrow r = 4 \\
$
The centre is at origin and the radius of the path is 4 units.
So in the given options,
The first equation is ${x^2} + {y^2} = 4$, here the centre is at the origin and the radius is ${r^2} = 4 \to r = 2$ units.
The second equation is the same as the path equation followed by the lion.
The third equation is ${x^2} + {y^2} - 64 = 0 \to {x^2} + {y^2} = 64$, here also the centre is at the origin and the radius is ${r^2} = 64 \to r = 8$ units.

So the first and the third path equations have different radii from the lion’s path radius and deer can save her life by following these paths.
So Option A and Option C are correct.
Hence, the correct option is Option D, both (a) and (c) are correct.
Note: Do not forget to write units of a measurement. If no units like metres, centimeters are given in the question then just write “units” after its value. And radius is always positive and will never be negative whereas the coordinates of the centre can be negative values.
Recently Updated Pages
Why is there a time difference of about 5 hours between class 10 social science CBSE

In cricket, what is a "pink ball" primarily used for?

In cricket, what is the "new ball" phase?

In cricket, what is a "death over"?

What is the "Powerplay" in T20 cricket?

In cricket, what is a "super over"?

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




