
A constant function is a periodic function.
A. True
B. False
Answer
526.8k+ views
Hint: We need to check whether the given statement is true or false. A periodic function can be defined as a function returning to the same value at regular intervals. A function $f$ is said to be periodic if, for some non-zero constant $P$ , it satisfies the equation, \[f\left( x+P \right)=\text{ }f\left( x \right)\] , for all values of $x$ in the domain . $P$ is the period of the function. A constant function, $f(x)=c$ repeats its values at regular intervals.
Complete step by step answer:
We need to check whether the statement “ a constant function is a periodic function” is true or false.
Let us see what a periodic function is.
A periodic function can be defined as a function returning to the same value at regular intervals.
For example, $\sin x$ .
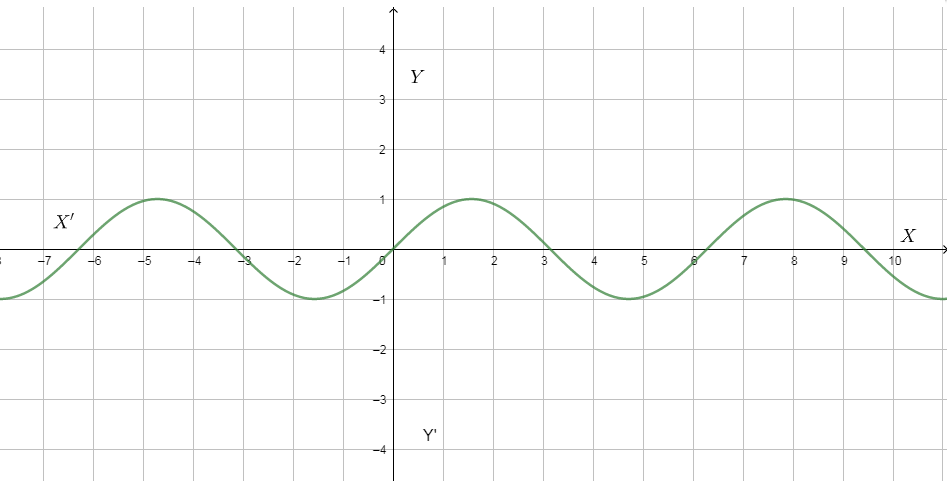
The function repeats continuously in a similar fashion. For example, from the figure, the wave begins from 0 to 3 goes to the negative part from 3 to 6. This fashion is repeated again.
A function $f$ is said to be periodic if, for some non-zero constant $P$ , it satisfies the equation, \[f\left( x+P \right)=\text{ }f\left( x \right)\] , for all values of $x$ in the domain . $P$ is the period of the function.
Constant function a real-valued function of a real-valued argument, denoted by $f(x)=c$ .
The below figure shows the graph of constant function $f(x)=2$ .
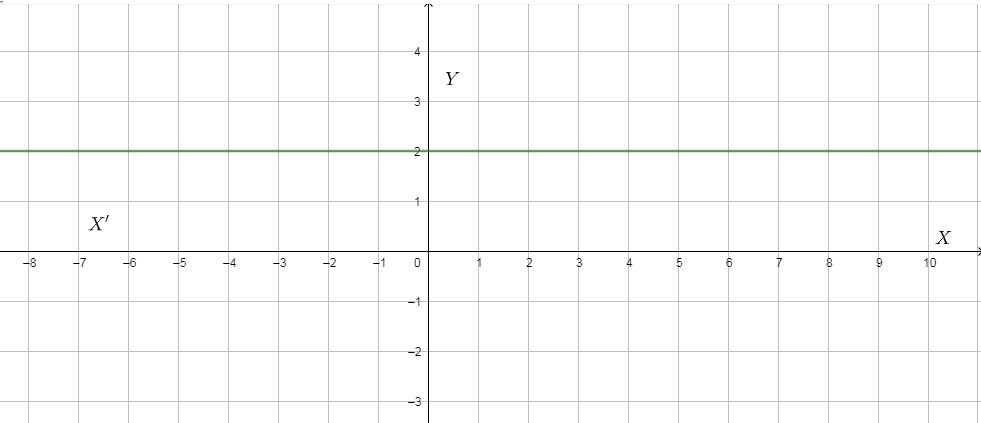
$f(x)=2$ repeats its values at regular intervals like for $x=1,2,....n$ , where $n=Z$ , an integer.
Hence, a constant function is a periodic function with a period $n$.
Hence, the given statement is True.
Note:
All constant functions are periodic irrespective of its type, that is, whether it is an integer, a fraction, or real number. \[f\left( x+P \right)=\text{ }f\left( x \right)\] is the equation of a periodic function. All constant functions repeat its values at regular intervals like for $x=1,2,....n$ , where $n=Z$ .
Complete step by step answer:
We need to check whether the statement “ a constant function is a periodic function” is true or false.
Let us see what a periodic function is.
A periodic function can be defined as a function returning to the same value at regular intervals.
For example, $\sin x$ .

The function repeats continuously in a similar fashion. For example, from the figure, the wave begins from 0 to 3 goes to the negative part from 3 to 6. This fashion is repeated again.
A function $f$ is said to be periodic if, for some non-zero constant $P$ , it satisfies the equation, \[f\left( x+P \right)=\text{ }f\left( x \right)\] , for all values of $x$ in the domain . $P$ is the period of the function.
Constant function a real-valued function of a real-valued argument, denoted by $f(x)=c$ .
The below figure shows the graph of constant function $f(x)=2$ .

$f(x)=2$ repeats its values at regular intervals like for $x=1,2,....n$ , where $n=Z$ , an integer.
Hence, a constant function is a periodic function with a period $n$.
Hence, the given statement is True.
Note:
All constant functions are periodic irrespective of its type, that is, whether it is an integer, a fraction, or real number. \[f\left( x+P \right)=\text{ }f\left( x \right)\] is the equation of a periodic function. All constant functions repeat its values at regular intervals like for $x=1,2,....n$ , where $n=Z$ .
Recently Updated Pages
NCERT Solutions For Class 4 English Marigold (Poem) - Don’t Be Afraid Of The Dark

NCERT Solutions For Class 5 English Marigold (Poem) - Class Discussion

NCERT Solutions For Class 5 English Marigold - Gullivers Travels

NCERT Solutions For Class 5 Hindi Rimjhim - Bagh Aaya Uss Raat

NCERT Solutions For Class 8 Hindi Bharat Ki Khoj - Tanaav

NCERT Solutions For Class 12 Maths - Differential Equations

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

When the President submits his resignation to the VicePresident class 10 social science CBSE

Five things I will do to build a great India class 10 english CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




