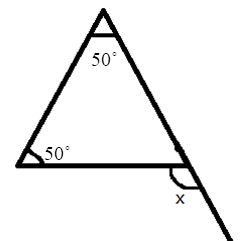The Triangle And Its Properties - Exercise-wise Questions and Answers For Class 7 Maths - Free PDF Download
FAQs on NCERT Solutions For Class 7 Maths Chapter 6 The Triangle And Its Properties - 2025-26
1. What are the main concepts I need to understand to solve the exercises in NCERT Class 7 Maths Chapter 6, 'The Triangle and Its Properties'?
To effectively solve the problems in the NCERT Solutions for Chapter 6, you must have a clear, step-by-step understanding of the following properties:
- Medians and Altitudes: Knowing the difference and how to identify them in a diagram.
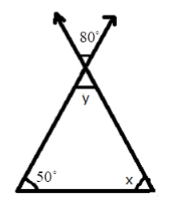
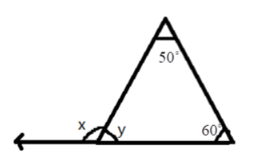
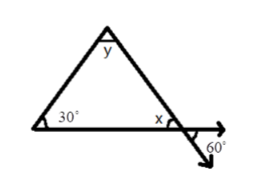
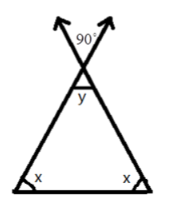
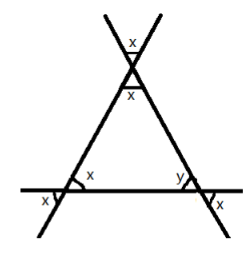
- Exterior Angle Property: The exterior angle of a triangle is equal to the sum of its interior opposite angles.
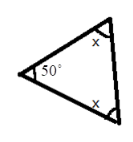
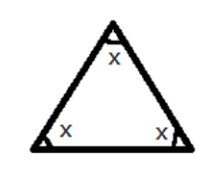
- Angle Sum Property: The sum of all three interior angles of any triangle is always 180°.
- Triangle Inequality Property: The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
- Pythagoras Theorem: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
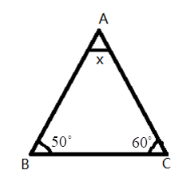
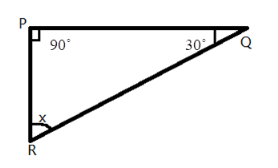
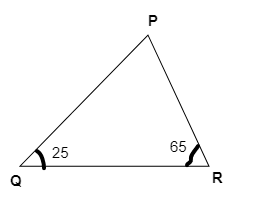
2. What is the correct method to find a missing angle in a triangle using the angle sum property, as shown in the NCERT solutions?
The NCERT solutions demonstrate a clear, step-by-step method:
- Identify Known Angles: Write down the measures of the two given angles of the triangle.
- Set Up the Equation: Use the angle sum property. Write the equation: Angle A + Angle B + Angle C = 180°.
- Substitute Values: Replace the known angles with their values in the equation. Let the unknown angle be 'x'.
- Solve for x: Add the known angles, then subtract their sum from 180° to find the value of the missing angle.
Following this procedure ensures you show all necessary steps for full marks.
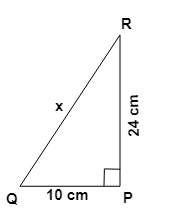
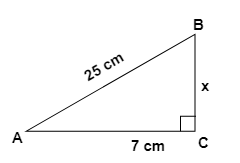
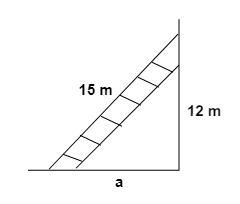
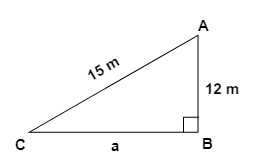
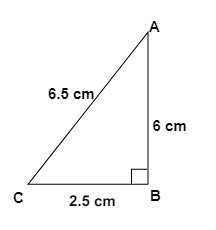
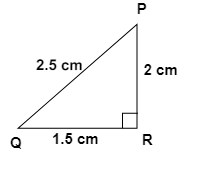
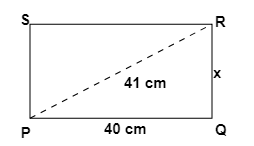
3. How do the NCERT Solutions guide students to apply the Pythagoras theorem to find a missing side in a right-angled triangle?
The NCERT Solutions for Chapter 6 provide a structured approach to applying the Pythagoras theorem:
- Step 1: Identify the right-angled triangle and correctly label its sides: the hypotenuse (the side opposite the 90° angle), the base, and the perpendicular.
- Step 2: State the Pythagoras theorem formula: a² + b² = c², where 'c' is the hypotenuse.
- Step 3: Substitute the lengths of the two known sides into the formula.
- Step 4: Perform the calculations to solve for the unknown side. If you are finding the hypotenuse, you will add the squares. If you are finding one of the other sides, you will subtract the square of the known side from the square of the hypotenuse.
- Step 5: Find the square root of the result to get the final length of the missing side.
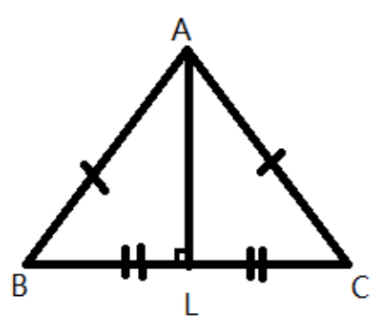
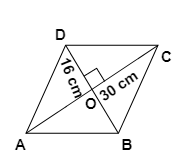
4. What is the difference between solving a problem with a median and one with an altitude, according to the methods in this chapter's NCERT solutions?
The key difference lies in the properties you use to solve the problem. In the NCERT solutions:
- A median connects a vertex to the midpoint of the opposite side. When solving a problem with a median (e.g., AD is a median to side BC), you use the property that it divides the side into two equal halves (BD = DC).
- An altitude connects a vertex to the opposite side at a 90° angle. When solving a problem with an altitude (e.g., AL is an altitude to side BC), you use the property that it forms a right-angled triangle (e.g., ΔALB or ΔALC), which often requires using the Pythagoras theorem or angle sum property.
Confusing these two can lead to using the wrong formula and an incorrect solution.
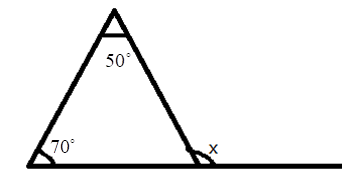
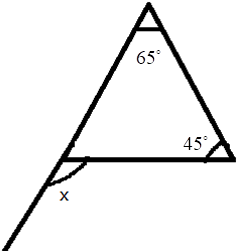
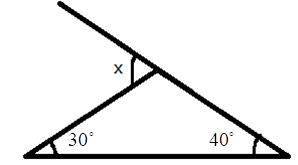
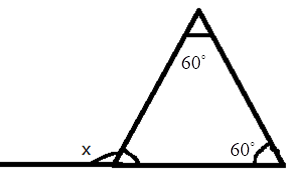
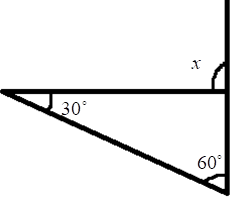
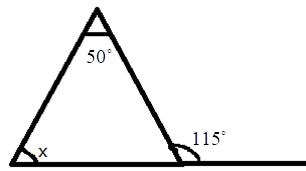
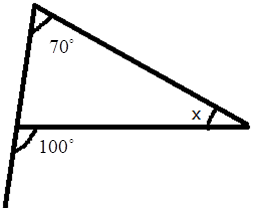
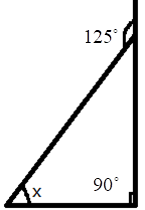
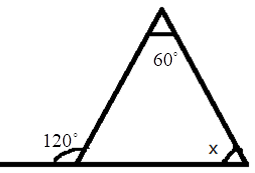
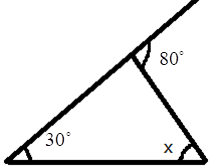
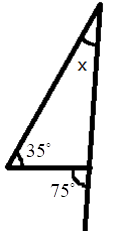
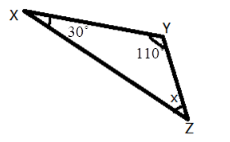
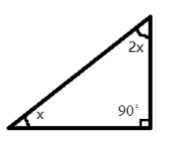
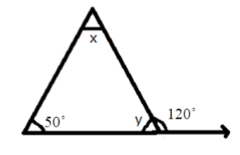
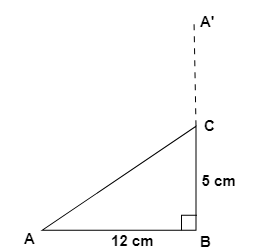
5. How do you find an unknown exterior angle of a triangle using the method in the NCERT solutions?
The NCERT solutions teach a direct method based on the Exterior Angle Property. The steps are:
- Identify the exterior angle and the two interior opposite angles. The interior opposite angles are the two angles inside the triangle that are not adjacent to the exterior angle.
- State the Property: Write down that the exterior angle is equal to the sum of the interior opposite angles.
- Form the Equation: Set up the equation by adding the measures of the two interior opposite angles.
- Calculate the Sum: The result of the addition is the measure of the unknown exterior angle.
6. How do the NCERT Solutions apply the triangle inequality theorem to verify if three given side lengths can form a triangle?
To check if a triangle is possible with three given side lengths, the NCERT solutions guide you to apply the triangle inequality theorem systematically. You must check three conditions:
- Sum of the first and second sides > Third side
- Sum of the second and third sides > First side
- Sum of the first and third sides > Second side
If all three of these conditions are true, then a triangle can be formed with those side lengths. If even one condition fails, it is not possible to form the triangle.
7. Why is it so important to correctly identify the 'interior opposite angles' when using the exterior angle property as shown in the solutions?
Correctly identifying the interior opposite angles is critical because the entire property depends on it. A common mistake students make is to add the adjacent interior angle to one of the opposite ones. The NCERT solutions methodology forces you to first locate the exterior angle, then deliberately find the two angles inside the triangle that are farthest from it. Using the wrong pair of angles will always lead to an incorrect answer. The property establishes a specific relationship, and misidentification breaks that relationship.
8. Why is following the detailed, step-by-step format from Vedantu's NCERT Solutions important for scoring full marks?
Following a detailed, step-by-step format is crucial for exams because it demonstrates your understanding of the underlying principles, not just the final answer. As per the CBSE pattern, marks are often allocated for:
- Stating the correct property or theorem (e.g., 'By Angle Sum Property').
- Setting up the equation correctly.
- Showing the calculation steps.
- Writing the final answer with the correct units.
Vedantu's solutions are designed to mirror this official marking scheme, helping you build the habit of showing all work and maximising your score.