Visualising Solid Shapes Class 7 Questions and Answers - Free PDF Download
Exercise 13.2
1. Use isometric dot paper and make an isometric sketch for each one of the
given shapes:
(i)
Ans: Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable.
(ii)
Ans: Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable.
(iii)
Ans: Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable.
(iv)
Ans: Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable.
2. The dimensions of a cuboid are 5 cm, 3 cm and 2 cm. Draw three different isometric sketches of this cuboid.
Ans: Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable.
The three different isometric sketches of this cuboid having dimension 5 cm, 3 cm and 2 cm is shown below,
3. Three cubes each with a 2 cm edge are placed side by side to form a cuboid. Sketch an oblique or isometric sketch of this cuboid.
Ans: Isometric Sketch
Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable
Isometric sketch of three cubes each with 2 cm edge are placed side by side to form a cuboid is given below,
Oblique sketch is a way of representing an object in pictorial form. Basically, the circles and angles parallel to the plane of projection are considered to be the true size and shape of the object while constructing oblique sketches.
Oblique sketch of three cubes each with 2 cm edge are placed side by side to form a cuboid is given below,
4. Make an oblique sketch for each one of the given isometric shapes:
(i)
Ans: Oblique sketch is a way of representing an object in pictorial form. Basically, the circles and angles parallel to the plane of projection are considered to be the true size and shape of the object while constructing oblique sketches.
Oblique sketch of given sketch is given below,
(ii)
Ans: Oblique sketch is a way of representing an object in pictorial form. Basically, the circles and angles parallel to the plane of projection are considered to be the true size and shape of the object while constructing oblique sketches.
Oblique sketch of given sketch is given below,
5. Give
(i) An oblique sketch
(a) A cuboid of dimensions 5 cm, 3 cm and 2 cm.
Ans: Oblique sketch is a way of representing an object in pictorial form. Basically, the circles and angles parallel to the plane of projection are considered to be the true size and shape of the object while constructing oblique sketches.
Oblique sketch of given sketch is given below,
(b) A cube with an edge 4 cm long.
Ans: Oblique sketch is a way of representing an object in pictorial form. Basically, the circles and angles parallel to the plane of projection are considered to be the true size and shape of the object while constructing oblique sketches.
Oblique sketch of given sketch is given below,
(ii) An isometric sketch for each of the following:
(a) A cuboid of dimensions 5 cm, 3 cm and 2 cm.
Ans: Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable
Isometric sketch of cuboid of dimensions 5 cm, 3 cm and 2 cm is given below,
(b) A cube with an edge 4 cm long.
Ans: Isometric Sketching is a representation of an object in which all the three-dimensions are drawn at the full scale. It looks like an isometric projection. In this case, all the lines parallel to its major axes are measurable.
Isometric sketch of cube with and edge 4 cm is given below,
NCERT Solutions for Class 7 Maths Chapter 13 Visualising Solid Shapes Exercise 13.2
Opting for the NCERT solutions for Ex 13.2 Class 7 Maths is considered as the best option for the CBSE students when it comes to exam preparation. This chapter consists of many exercises. Out of which we have provided the Exercise 13.2 Class 7 Maths NCERT solutions on this page in PDF format. You can download this solution as per your convenience or you can study it directly from our website/ app online.
Vedantu in-house subject matter experts have solved the problems/ questions from the exercise with the utmost care and by following all the guidelines by CBSE. Class 7 students who are thorough with all the concepts from the Subject Visualising Solid Shapes textbook and quite well-versed with all the problems from the exercises given in it, then any student can easily score the highest possible marks in the final exam. With the help of this Class 7 Maths Chapter 13 Exercise 13.2 solutions, students can easily understand the pattern of questions that can be asked in the exam from this chapter and also learn the marks weightage of the chapter. So that they can prepare themselves accordingly for the final exam.
Besides these NCERT solutions for Class 7 Maths Chapter 13 Exercise 13.2, there are plenty of exercises in this chapter which contain innumerable questions as well. All these questions are solved/answered by our in-house subject experts as mentioned earlier. Hence all of these are bound to be of superior quality and anyone can refer to these during the time of exam preparation. In order to score the best possible marks in the class, it is really important to understand all the concepts of the textbooks and solve the problems from the exercises given next to it.
Do not delay any more. Download the NCERT solutions for Class 7 Maths Chapter 13 Exercise 13.2 from Vedantu website now for better exam preparation. If you have the Vedantu app in your phone, you can download the same through the app as well. The best part of these solutions is these can be accessed both online and offline as well.
Class 7 Maths Chapter 13: Exercises Breakdown
CBSE Class 7 Maths Chapter 13 Other Study Materials
Chapter-Specific NCERT Solutions for Class 7 Maths
Given below are the chapter-wise NCERT Solutions for Class 7 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Important Related Links for NCERT Class 7 Maths
Access these essential links for NCERT Class 7 Maths, offering comprehensive solutions, study guides, and additional resources to help students master language concepts and excel in their exams.
FAQs on NCERT Solutions For Class 7 Maths Chapter 13 Visualising Solid Shapes Exercise 13.2 - 2025-26
1. Where can I find the correct step-by-step NCERT Solutions for Class 7 Maths Chapter 13, Visualising Solid Shapes?
You can find detailed, step-by-step NCERT Solutions for all exercises in Class 7 Maths Chapter 13 right here on Vedantu. These solutions are prepared by subject matter experts and strictly follow the CBSE 2025-26 syllabus and guidelines to ensure you learn the correct problem-solving methods.
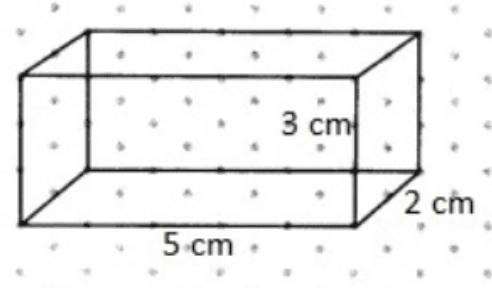
2. What is the correct method for drawing an isometric sketch of a cuboid as shown in the NCERT solutions?
The correct method for drawing an isometric sketch of a cuboid involves using an isometric dot sheet. The steps are:
- Start by drawing a rectangle for the front face.
- Draw lines backwards and upwards from the corners of the rectangle. These lines should be parallel and of equal length.
- Connect the ends of these lines to form the back face of the cuboid.
- Ensure all lines representing the length, breadth, and height follow the dot grid to maintain proportions.
3. How do the NCERT Solutions for Chapter 13 explain how to identify the different views of a solid shape?
The NCERT Solutions explain this by demonstrating a clear, methodical approach. To identify the top, front, and side views, you must imagine looking at the 3D object from that specific direction. For example, the front view is what you see when you look at the object head-on, the top view is what you see from directly above, and the side view is what you see from the side. The solutions provide solved examples with diagrams for various solids.
4. What key concepts are covered in the NCERT Solutions for Exercise 13.1 of Visualising Solid Shapes?
The NCERT Solutions for Exercise 13.1 primarily focus on identifying different nets that can be used to make cubes. The solutions provide a step-by-step verification method for each given net, showing how it can (or cannot) be folded to form a cube without any overlapping faces.
5. How can I use the NCERT solutions to verify Euler's formula for polyhedrons?
The NCERT Solutions guide you to verify Euler's formula (F + V - E = 2) systematically. For any given polyhedron, the correct method is:
- Step 1: Count the total number of faces (F).
- Step 2: Count the total number of vertices (V), which are the corners.
- Step 3: Count the total number of edges (E).
- Step 4: Substitute these values into the formula F + V - E. If the result is 2, the formula is verified for that shape.
6. Why is it important to draw solid shapes on an isometric dot sheet instead of plain paper when following the NCERT method?
Using an isometric dot sheet is crucial because it helps in drawing 3D objects with a more realistic sense of proportion and depth. Unlike plain paper, the dots are arranged in a triangular pattern, which allows you to easily draw lines at 60-degree angles to represent the three dimensions (length, width, height) accurately, making the sketch look three-dimensional as intended by the CBSE curriculum.
7. Beyond just getting the correct answer, what is the main purpose of solving problems on 'nets' in Chapter 13?
The main purpose of solving problems on nets is to develop your spatial reasoning and visualisation skills. By mentally folding a 2D net into a 3D shape, you learn to understand the relationship between two-dimensional representations and the three-dimensional objects they form. This skill is fundamental in fields like engineering, architecture, and design.
8. How do the problem-solving techniques for oblique sketches differ from those for isometric sketches in the NCERT solutions?
The key difference lies in how they represent 3D objects on a 2D plane.
- Oblique sketches are easier to draw; the front face is drawn true to its shape, and the depth is shown with parallel lines going back at an angle. However, they can look distorted.
- Isometric sketches provide a more realistic view where all dimensions are drawn to scale, but they require an isometric dot sheet for accuracy.
9. Can a single 3D shape, like a cube, have more than one correct net? How do the NCERT solutions handle this?
Yes, a single 3D shape can have multiple correct nets. For instance, a cube has 11 different possible nets. The NCERT solutions address this by presenting various configurations in the exercises and asking you to identify which ones will successfully fold into the shape. The solution for each problem provides a clear, step-by-step logical explanation for why a particular net works or fails.
