




How to Plot Points Using X and Y Coordinates
Have you ever thought about how you would represent a point (2,3)? This is done using a coordinate plane which is defined as a two-dimensional plane formed by the intersection of two lines, a vertical line called the y-axis and a horizontal line called the x-axis. These lines are perpendicular to each other, intersecting at a point called the origin. The given article covers all the concepts of coordinates, using attractive images to grab student's attention in learning. Students having a grip on this topic will be able to understand coordinate geometry easily.
Showing X and Y Coordinate Plane
What are Coordinates?
Coordinates are a pair of numbers written in an ordered pair that identifies a specific point on a coordinate plane. Coordinates are represented using the ordered pair (x, y), which corresponds to the x and y coordinates, respectively. These coordinates can be positive, negative, or zero depending on the quadrant in which it lies.
Grid for Coordinates
A coordinate grid is a two-dimensional surface, which represents a regular arrangement in which the horizontal lines of the x-axis intersect with the vertical lines of the y-axis to form regular blocks, resembling fishing nets. The point of the intersection of horizontal and vertical lines forms a right angle, i.e. an angle perpendicular to each other.
Coordinates Grid
Quadrants of the Grid for Coordinates
Quadrants are defined as that region of the plane which is gained after the intersection of the two axes. There are four quadrants in the grid for coordinates: namely,
First Quadrant
Here, both the x and y coordinates are positive. For example: (2,3).
Second Quadrant
Here, the x coordinate is negative and the y coordinate is positive. For example: (-1,3).
Third Quadrant
Here, both the x and y coordinates are negative. For example: (-1,-5).
Fourth Quadrant
Here, the x coordinate is positive and the y coordinate is negative. For example: (6,-8).
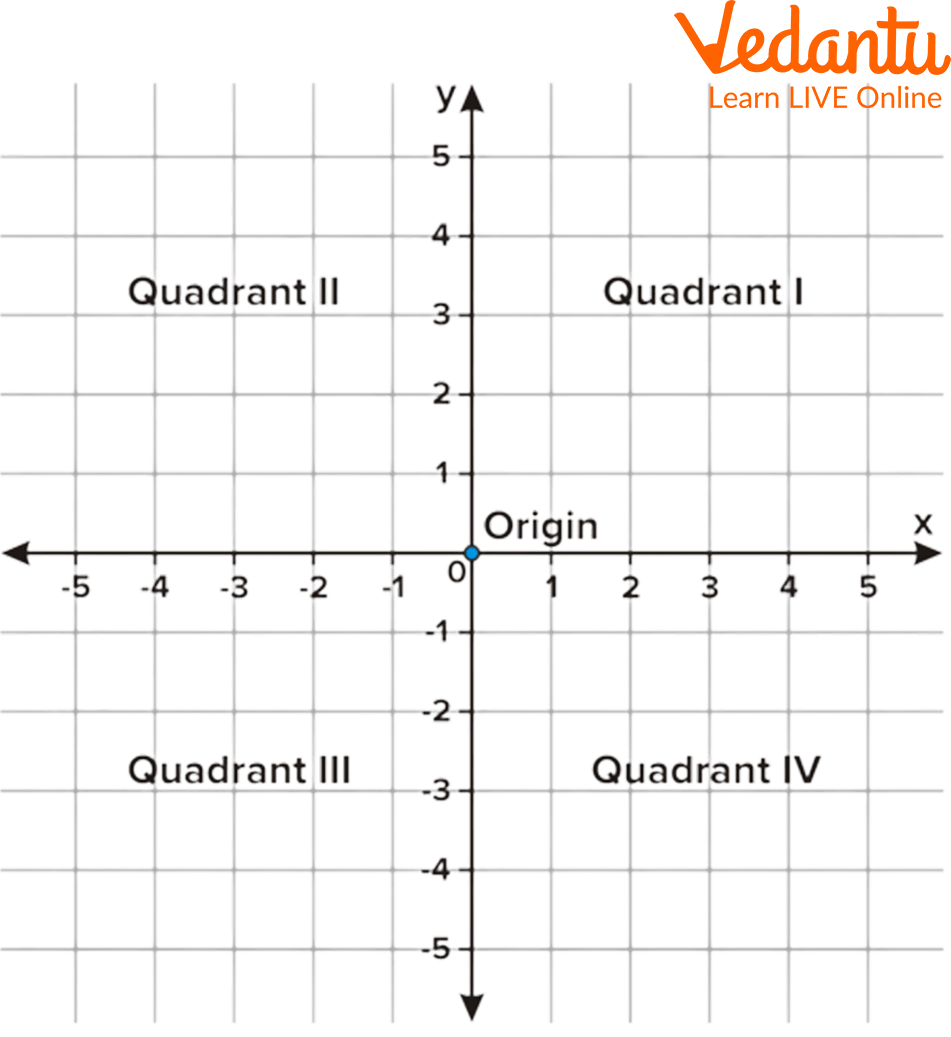
Four Quadrants of a Grid of Coordinates
How to Write Coordinates
Coordinates are written in an ordered form inside the brackets, separating each other with commas i.e. (x,y). The first term in the coordinate specifies the point on the x-axis and the second term specifies the point on the y-axis. Coordinate examples are: (3,4), (-3,-6), (6,-2), etc.
Locating X and Y Coordinates
To locate xy coordinates on the graph, one needs to follow some steps:
Read the coordinate and find out in which quadrant it lies.
Mark the x and y coordinates in the respective quadrant.
Highlight the point and write the coordinates.
Solved Coordinate Examples
Some coordinate examples are discussed underneath:
Q1. Plot (-3,2) on xy coordinates graph.
Ans: Using a simple series of steps to plot a point on the coordinate plane:
Read the coordinate, (-3,2) and find out in which quadrant it lies, i.e. 2nd quadrant
Mark the value of x=-3 and y=2 in the respective quadrant
Highlight the point and write its coordinates

Coordinates Images
Q2. Plot (4,2), (-3,4), (-4,0), (0,-5) on xy coordinates graph.
Ans: Using a simple series of steps to plot these points on the xy coordinate graph:
Read one of the given coordinates, say (4,2) and find out in which quadrant it lies, i.e. 1st quadrant.
Mark x=4 and y=2 in the respective quadrant.
Highlight the point and write its coordinate.
Repeat the above process for all other given points.
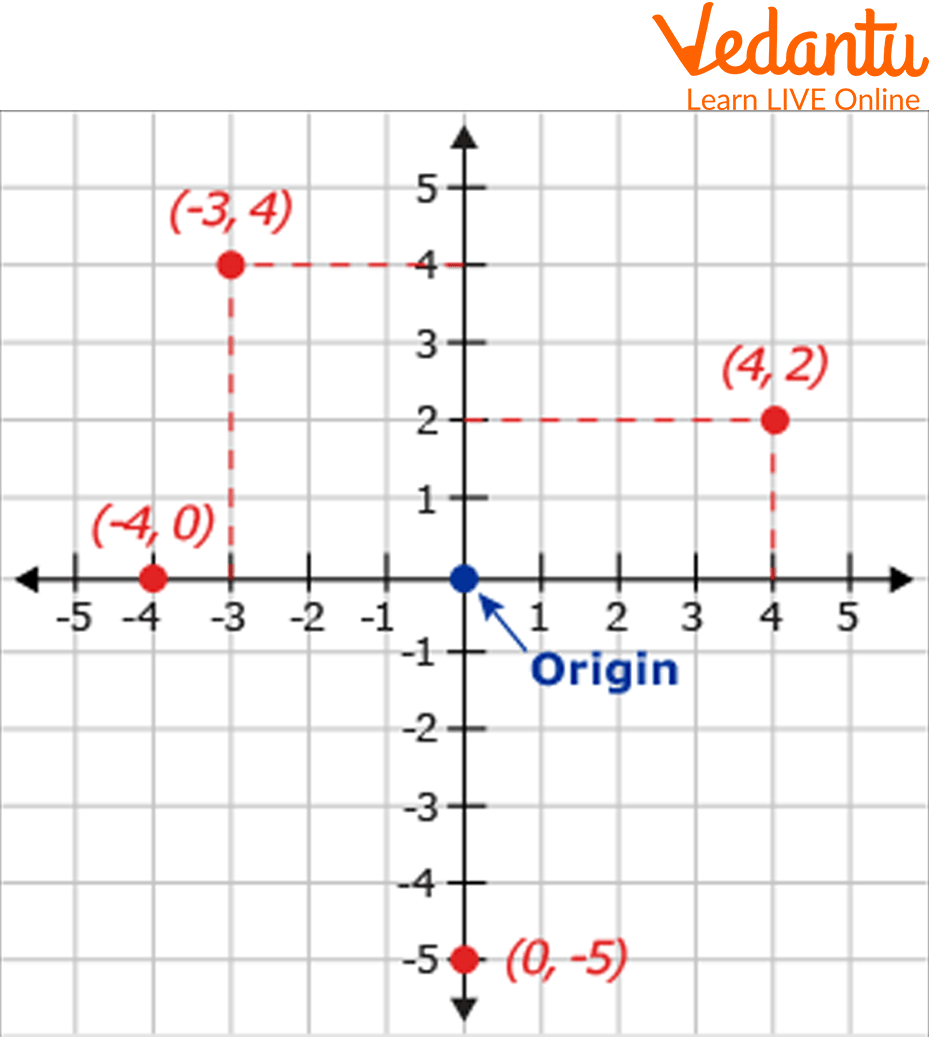
Coordinates Images
Practice Problems
Q1. Locate (5,6) on the coordinate graph.
Q2. Plot (-3.5,-2) on the XY coordinate graph.
Q3. Locate (2,-3) on the coordinate grid.
Q4. Show (-3,7) on the grid for coordinates.
Summary
Summing up here with the concept of coordinates. This article covers the topics of grid for coordinates, quadrants, and x and y coordinates using a unique way that will have the students in gaining better. Here we have discussed in depth how to write the coordinates and how to locate them on the xy coordinate graph. Some practice problems along with solved examples have been shared so that students can practise well and gain proficiency in the concept deeply.
FAQs on Understanding X and Y Coordinates in Maths
1. What are coordinates in mathematics?
In mathematics, coordinates are a set of two numbers, written as an ordered pair (x, y), that specify the exact position of a point on a plane. This plane, known as the Cartesian plane or coordinate plane, is formed by two perpendicular number lines: the horizontal x-axis and the vertical y-axis. The first number represents the horizontal distance, and the second represents the vertical distance from a central reference point.
2. What are the specific names for the x-coordinate and y-coordinate?
The two components of a coordinate pair have specific names based on the axis they correspond to. The x-coordinate is called the abscissa, which indicates the point's horizontal position. The y-coordinate is called the ordinate, which indicates its vertical position.
3. How is a point represented using coordinates on a graph?
To represent a point like (4, 3) on a graph, you always start at the origin (0, 0). First, you move along the horizontal x-axis by the value of the abscissa (4 units to the right). From that spot, you move parallel to the vertical y-axis by the value of the ordinate (3 units up). The spot where you land is the precise location of the point (4, 3).
4. Why is the order of numbers in a coordinate pair, like (2, 5), so important?
The order is crucial because coordinates are an ordered pair, meaning the sequence has a specific meaning. The first number always represents the x-value (horizontal movement), and the second always represents the y-value (vertical movement). For example, the point (2, 5) is located 2 units right and 5 units up. If you swap the order to (5, 2), you get a completely different location: 5 units right and 2 units up. The fixed order ensures every point has a unique address.
5. What is the significance of the origin, or the point (0, 0), in the Cartesian plane?
The origin (0, 0) is the most important reference point in the Cartesian plane. It is the exact location where the x-axis and y-axis intersect. It serves as the universal starting point for all measurements, and every other coordinate is essentially a set of directions on how far to move horizontally and vertically from this origin to reach a specific point.
6. Could you give some real-world examples of how coordinates are used?
Coordinates are fundamental for defining locations in many real-world systems. Common examples include:
- Game Design: Characters and objects in video games are placed and moved using a coordinate system to define their position on the screen.
- Computer Graphics: Every pixel on a monitor has a coordinate to determine its precise position and colour.
- Mapping and Navigation: GPS systems use a global coordinate system (latitude and longitude) to pinpoint exact locations on Earth.
- Chess: Each square on a chessboard is identified by a unique coordinate pair, like 'e4', which combines a letter and a number.
7. What is coordinate geometry and how does it use coordinates?
Coordinate geometry is a powerful branch of mathematics that combines algebra and geometry. It uses coordinates to represent geometric figures—such as lines, circles, and triangles—as equations on the Cartesian plane. By using coordinates, we can algebraically calculate key properties like the distance between two points, the slope of a line, or the area of a polygon, effectively turning geometric problems into algebraic ones.
8. Are there other types of coordinate systems besides the standard x-y grid?
Yes, while the Cartesian (x-y) system is the most common in school-level mathematics, other systems exist for different applications. For example:
- The Polar Coordinate System describes a point's location using a distance from a central point and an angle.
- Three-dimensional (3D) systems, like the Cartesian (x, y, z) system, add a third axis (the z-axis) to describe the position of points in space, not just on a flat plane.









