Straight Line Definition Properties and Equation with Examples
The line definition, as stated by Euclid, basically states that a straight line connects any two given points and can be extended forever in both directions. The shortest distance between two points is a straight line.
A straight line is a continuous, one-dimensional shape with no breadth. It consists of an infinite number of points connected on either side of a point. It might be inclined, vertical, or horizontal. Any angle we draw between two locations along a straight line will always be a 180-degree angle.
What is a Straight Line?
A straight line has no curvature. A straight line can also be drawn between any two points, but its endpoints must stretch into the infinite. When two points, A (x1, y1) and B (x2, y2) are connected by the shortest path possible, a straight line is a result. We see straight lines in our day-to-day life, such as railway tracks, Roads, and Bridges.
Straight Line
Types of Straight Lines
There are several kinds of straight lines. The alignment of the straight lines is typically used to categorise them. The angle they make with either the x-axis or the y-axis is referred to as their alignment. Straight lines can be classified into the following categories based on their alignment:
Horizontal Lines
Vertical Lines
Oblique/Inclined Lines
Horizontal Lines
Horizontal lines are parallel to the x-axis or perpendicular to the y-axis when drawn horizontally. They intersect the x-axis at an angle of 0° or 180° and the y-axis at an angle of 90° or 270°. This line does not touch any point on the X-axis. All the points on this line will have the same Y-coordinate.
Horizontal Line
Vertical Lines
Vertical lines are drawn vertically and parallel to the y-axis or perpendicular to the x-axis. They intersect the x-axis at an angle of 90° or 270° and the y-axis at an angle of 0° or 180°. All the points on this line will have the same X-coordinate.
Vertical Lines
Oblique/Inclined Lines
Oblique or slanting lines are those that are drawn at an angle other than 0°, 90°, 180°, 270°, or 360° with the horizontal or vertical lines. Oblique or inclined lines are straight lines that are neither horizontal nor vertical.
Oblique Lines
Properties of Straight Lines
The properties of straight lines are illustrated below:
A straight line can go on forever. The distance between the line's two extreme points is impossible to measure.
It has no volume and no areas. However, its length is unlimited.
It is a figure with only one dimension.
A single point can be traversed by an endless number of lines, but only one single line can pass between two points.
Equation of a Straight Line
An equation of a straight line is a linear equation. Depending on the known variables, angles, and constants, a straight line on a plane can be represented in a variety of ways. The direction of a straight line is determined by its slope, which also indicates how steep the line is. It is calculated as the difference in y coordinates/difference in x coordinates and is also referred to as rise over run. There are several ways to write a straight-line equation.
General Equation of a Straight Line
The general formula for a straight line is $ax + by + c = 0$, where
The slope will be $\dfrac{{ - a}}{b}$.
Here, a, b, and c are constants, and x, and y are variables.
Slope Point Form:
The idea of calculating a line's slope from two points is the basis of the slope-point form. A straight line going through the point $\left( {{x_1},{y_1}} \right)$ and having a slope of $m = \tan \theta $, where $\theta $ is the angle produced by the line with the positive x-axis is given as $(y - {y_1}) = m(x - {x_1})$
Slope point form
Two-Point Form:
When two points along a line are known, the equation of the line may be found using the two-point form. Given by is a straight line that connects the coordinates $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$. The two-point form is: $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}(x - {x_1})$
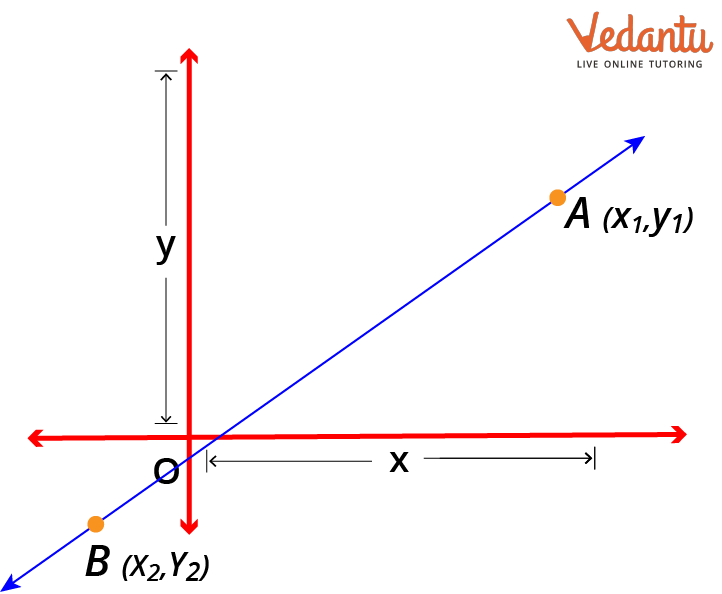
Two-point form
Intercept Form:
The point where the graph crosses the axes is known as the intercept. The point where the graph meets the x-axis is known as the x-intercept if the graph crosses the x-axis. The point at which a graph contacts the y-axis is referred to as the y-intercept. The intercept form of a straight line with point A on the x-axis and point B on the y-axis, as seen in the picture below, is expressed as a straight line with the x-intercept as a and y-intercept as b. The intercept form is: $\dfrac{x}{a} + \dfrac{y}{b} = 1$
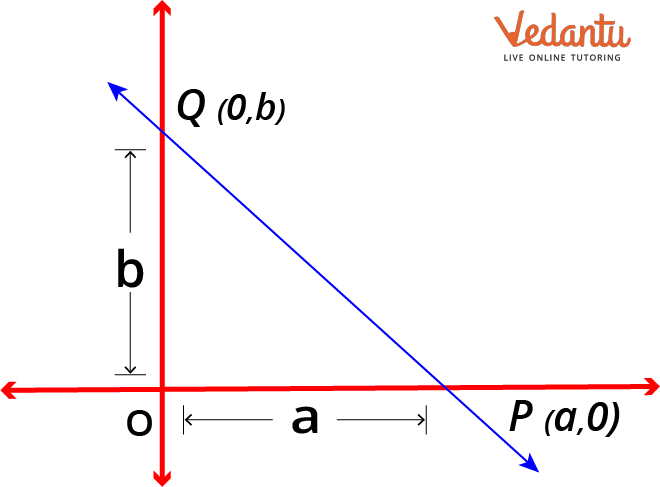
Intercept form
Straight Line Problems:
Let us look at some straight line questions and answers or Problems on Straight Lines:
Example 1: What will be the equation of the line passing through the points (2,3) and (5,4)?
Solution: To find the equation of a line passing through the points (2,3) and (5,4), we will use the two-point form:
$y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}(x - {x_1})$
Substituting the values, we get
$\begin{array}{l}y - 3 = \dfrac{{4 - 3}}{{5 - 2}}(x - 2)\\3y - 9 = x - 2\\3y - x - 7 = 0\end{array}$
Therefore, the equation of a line is $3y - x - 7 = 0$.
Example 2: What is the equation of the line which has a slope of 3 and passes through a point (2,5)?
Solution: To find the equation of the line with slope 3 and passing through a point (2,5) we will use slope point form:
$(y - {y_1}) = m(x - {x_1})$
Substituting the values,
$\begin{array}{l}y - 5 = 3(x - 2)\\y - 5 = 3x - 6\\y - 3x + 1 = 0\end{array}$
Conclusion:
We now have a basic understanding of the line and its key components due to this article. We will be able to apply the principles to real-world applications and discover more fascinating facts about the line using the many sorts of lines that have been discussed in this article.
FAQs on What Is a Straight Line in Geometry
1. What is a straight line in maths?
A straight line is a one-dimensional figure that extends infinitely in both directions without any curvature. In geometry, it has only length and no width or thickness. It is the shortest distance between two points and has a constant direction throughout. In coordinate geometry, a straight line is usually represented by a linear equation such as y = mx + c.
2. What is the equation of a straight line?
The most common equation of a straight line is y = mx + c, where m is the slope and c is the y-intercept. Other forms include:
- Standard form: ax + by + c = 0
- Point-slope form: y − y₁ = m(x − x₁)
- Two-point form: (y − y₁)/(y₂ − y₁) = (x − x₁)/(x₂ − x₁)
These forms are used in coordinate geometry to represent linear equations.
3. What is the slope of a straight line?
The slope of a straight line measures its steepness and is defined as the change in y divided by the change in x. The formula is m = (y₂ − y₁)/(x₂ − x₁). If m > 0, the line rises from left to right; if m < 0, it falls; and if m = 0, the line is horizontal.
4. How do you find the equation of a straight line given two points?
To find the equation of a straight line through two points, first calculate the slope and then use the point-slope form. Steps:
- Find slope: m = (y₂ − y₁)/(x₂ − x₁)
- Use point-slope form: y − y₁ = m(x − x₁)
Example: For points (1,2) and (3,6), m = (6−2)/(3−1) = 4/2 = 2. Equation: y − 2 = 2(x − 1), which simplifies to y = 2x.
5. What is the difference between a line, line segment, and ray?
The difference lies in how far they extend.
- Line: Extends infinitely in both directions.
- Line segment: Has two fixed endpoints.
- Ray: Has one endpoint and extends infinitely in one direction.
All three are straight, but only a line has no endpoints.
6. What is the shortest distance between two points?
The shortest distance between two points is a straight line. In coordinate geometry, the distance between points (x₁, y₁) and (x₂, y₂) is given by √[(x₂ − x₁)² + (y₂ − y₁)²]. This formula comes from the Pythagorean theorem.
7. What are the properties of a straight line?
A straight line has several key properties in geometry:
- It has only length and no width.
- It extends infinitely in both directions.
- It has a constant slope.
- The angle between two intersecting straight lines can be calculated using slope formulas.
These properties are fundamental in coordinate geometry and linear equations.
8. What is the angle between two straight lines?
The angle θ between two straight lines with slopes m₁ and m₂ is given by tanθ = |(m₂ − m₁)/(1 + m₁m₂)|. If m₁m₂ = −1, the lines are perpendicular. This formula is widely used in coordinate geometry to find the angle between linear equations.
9. What does a horizontal or vertical straight line look like?
A horizontal line has equation y = constant, and a vertical line has equation x = constant. A horizontal line has slope 0, while a vertical line has an undefined slope. These are special cases of straight lines in the Cartesian plane.
10. Where are straight lines used in real life?
Straight lines are used in real life to model constant relationships and shortest paths. Examples include:
- Roads and railway tracks (shortest route).
- Graphs of constant speed in physics (linear graphs).
- Architecture and construction design.
- Linear cost and profit functions in economics.
In mathematics, straight lines form the basis of linear equations and coordinate geometry.
