




Sequence: Observing the Logic in Every Pattern
Do you know how to predict which number comes next in a series of numbers? Well, patterns are all around us. Patterns can be repeated items, shapes, colours, images, or numbers. Sometimes a set of things is repeated to create a pattern. Number patterns are fun because you need to look carefully for clues to complete them. If you are intrigued and want to know what number sequence is or how you can identify a pattern, continue reading through the content below.
So, what is the number sequence? Let’s understand with the help of simple activities given below.
Activity
Here is a number pattern, or a sequence of numbers. Find out what comes next?
1, 2, 3, 4, 5, __
This is a fairly easy pattern because we count this one all the time. It’s 6.
The number 6 completes this pattern.
Here is another one.
Let’s find the next number by following the pattern 2, 4, 6, 8, ___.
We have 2, 4, 6, 8. If you look for clues, we see that each number in this sequence exceeds its previous number by 2. That’s the clue.
⇒ 2 + 2 is 4.
⇒ 4 + 2 is 6.
⇒ 6 + 2 is 8.
We should add 2 to 8 to give us the next number. Therefore, the next number is 10.
Number patterns can also work in reverse.

Number Pattern
When you look closely, you will see that the numbers are decreasing. It means that in this pattern, the numbers are not adding on. It's subtracting.
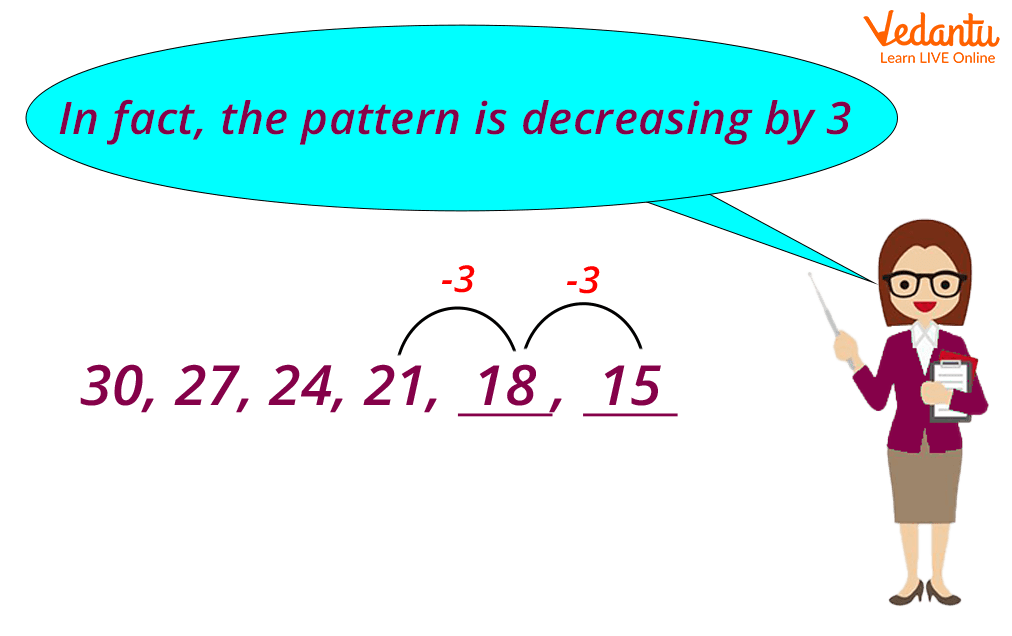
Number Pattern
30 − 3 is 27.
27 − 3 is 24.
24 − 3 is 21.
21 − 3 is 18.
81 − 3 is 15.
Things to Remember
Number pattern: These are the numbers that follow a particular sequence or pattern.
Growing pattern: If the numbers are getting bigger, then it is a growing pattern.
Shrinking pattern: If the numbers are getting smaller, then it will be a shrinking pattern.
Repeating pattern: When the same number grouping is observed over and over again.
Types of Sequences
There are different types of sequences based on the pattern among the terms. The following are the most familiar sequences.
1. Arithmetic Sequence:
In an arithmetic sequence, the common difference between any two successive terms remains the same. Note the common difference can be either negative or positive.
For example: 5, 10, 15, 20, 25, 30, ...
In this example, the common difference between any two successive terms is 5.

Arithmetic Sequence
2. Geometric Sequence:
A geometric sequence is one in which the common ratio of any two successive terms is the same. Multiplying the first term with the common ratio gives the second term and multiplying the second term with the common ratio gives the third term and so on.
For example: 2, 4, 8, 16, 32, 64…
Here, the common ratio between any two successive terms is 2.
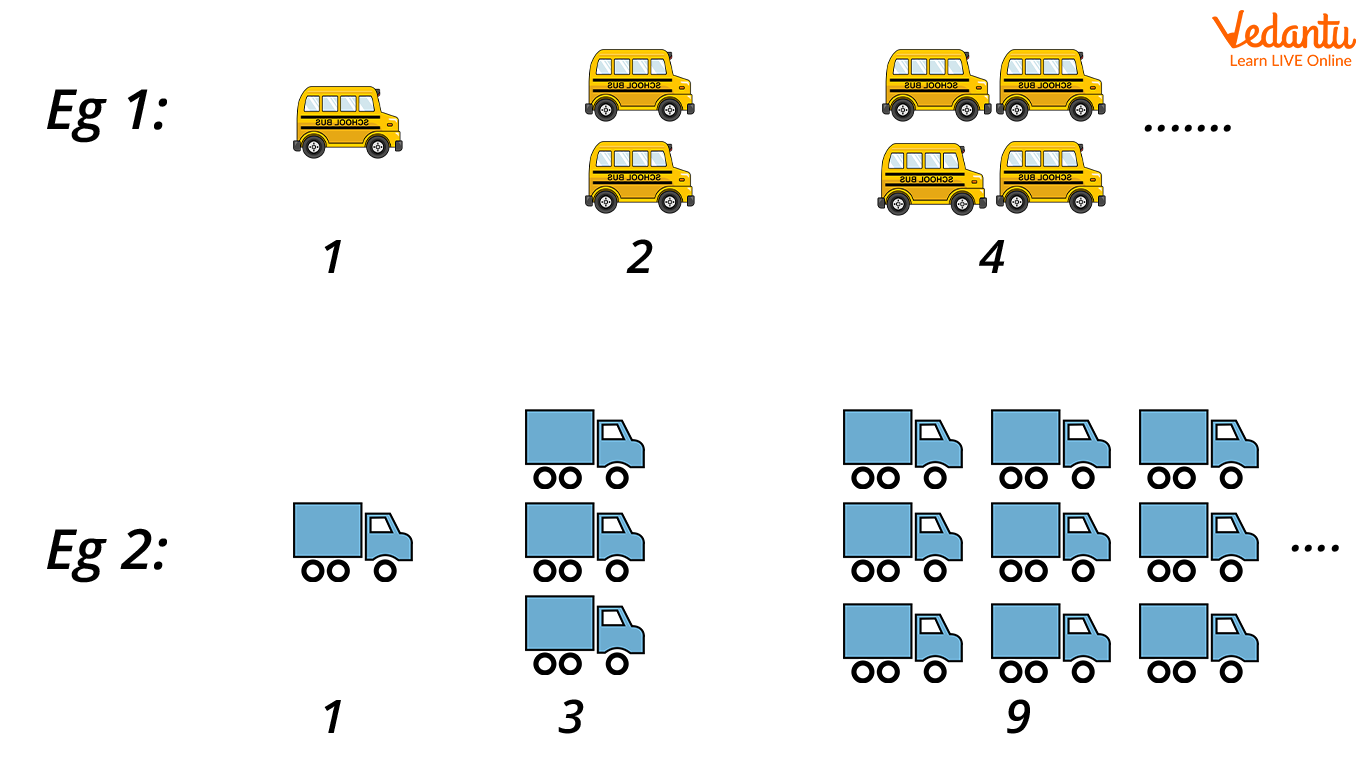
Geometric Sequence
3. Harmonic Sequence:
A sequence is said to be a harmonic sequence if the reciprocals of the terms are in an arithmetic sequence.
For example: $\frac{1}{5}, \frac{1}{10}, \frac{1}{15}, \frac{1}{20}, \frac{1}{25}, \frac{1}{30},....$
If you take the reciprocals of each term in this sequence, we get 5, 10, 15, 20, 25, 30, … which are in an arithmetic sequence.
4. Fibonacci Sequence:
Fibonacci numbers are a fascinating number series in which each element is created by adding two preceding elements, with the sequence beginning with 0 and 1. The first term is 0 and the second term is 1. The third term will be obtained by adding the first and second term which is equal to 0+1 = 1. The fourth term will be equal to the sum of the third and second terms, i.e., 1 + 1 = 2, and so on.
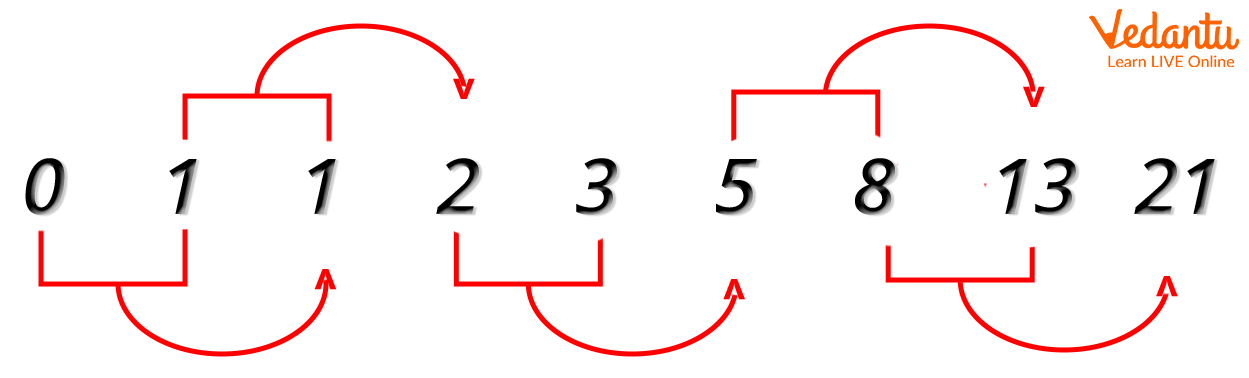
Fibonacci Sequence
Conclusion
Number sequencing is a process in a child's development of number sense. This is because it involves calculating, thinking, and reasoning. The steps, however, can be confusing to children. So, rather than forcing children to take a compulsive learning course, we can involve them in pleasant games and activities to make learning easier. Children can master arithmetic reasoning if they are familiar with numerical sequencing. To teach your young ones similar Maths topics in a fun way and help create a strong mathematical base, visit our website now.
FAQs on What is a Sequence?
1. What is a sequence in mathematics, with an example?
In mathematics, a sequence is an ordered list of numbers that follow a specific rule or pattern. Each number in the list is called a term, and each term has a unique position (first, second, third, and so on). For example, the set of numbers 5, 10, 15, 20, ... is a sequence where the rule is to add 5 to the previous term.
2. What are the main types of sequences explained in the NCERT syllabus?
The primary types of sequences students learn about as per the CBSE syllabus are:
- Arithmetic Sequence: A sequence where the difference between any two consecutive terms is constant. This constant is called the common difference. Example: 4, 7, 10, 13, ... (common difference is 3).
- Geometric Sequence: A sequence where the ratio of any two consecutive terms is constant. This constant is called the common ratio. Example: 2, 6, 18, 54, ... (common ratio is 3).
- Fibonacci Sequence: A special sequence where each term is the sum of the two preceding ones, starting from 0 and 1. Example: 0, 1, 1, 2, 3, 5, 8, ...
3. How can you tell the difference between a finite and an infinite sequence?
The key difference is whether the sequence has an end. A finite sequence contains a specific, limited number of terms and has a defined last term. For instance, the sequence of marks from 5 tests is finite. An infinite sequence continues without end and has no last term, which is usually indicated by ellipses (...). For example, the sequence of all natural numbers (1, 2, 3, ...) is infinite.
4. What is the important difference between a sequence and a series?
This is a common point of confusion for students. A sequence is simply an ordered list of numbers (e.g., 2, 4, 6, 8). A series, on the other hand, is the sum of the terms in a sequence (e.g., 2 + 4 + 6 + 8). In simple terms, a sequence is the list, and a series is the result of adding up that list.
5. What does the 'general term' or 'n-th term' of a sequence represent?
The general term (often written as aₙ) is a mathematical formula that defines the rule of the sequence. It allows you to calculate any term in the sequence by simply substituting its position number 'n' into the formula. For example, in the sequence of even numbers 2, 4, 6, 8, ..., the general term is aₙ = 2n. Using this, you can quickly find the 50th term (a₅₀ = 2 * 50 = 100) without listing all the terms before it.
6. How are mathematical sequences used in real-world applications?
Sequences are fundamental to modelling patterns in the real world. Some common applications include:
- Finance: Calculating compound interest or loan repayments over time, which often follow a geometric sequence.
- Biology: Modelling population growth or the decay of radioactive substances.
- Computer Science: Algorithms and data structures often rely on ordered sequences.
- Nature: The Fibonacci sequence famously appears in the arrangement of petals on a flower and spirals on a pinecone.
7. Is it possible for a sequence to be both arithmetic and geometric?
Yes, a sequence can be both arithmetic and geometric, but only under a very specific condition. This occurs when the sequence is a constant sequence of non-zero numbers, for example, 7, 7, 7, 7, ... In this case, the common difference is 0 (making it arithmetic), and the common ratio is 1 (making it geometric). A sequence of all zeros is only considered arithmetic, as division by zero for the common ratio is undefined.









