




Introduction to Solid Geometry
In geometry, the figure that deals with three-dimensional shapes is known as a 3D shape or a solid shape.
The conventional name for the geometry of three-dimensional Euclidean spaces (also known as 3D geometry) in mathematics is "solid geometry," sometimes known as "stereometry."
Measurements of the volumes of different solid forms (or 3D shapes), such as cylinders, pyramids, prisms, and other polyhedrons, cones, truncated cones, and balls enclosed by spheres, are the subject of stereometry. The whole concept is known as solid geometry. In solid geometry, there are so many types of solids.
Solid Geometry Definition:
Solids come in many different varieties in terms of geometry. Because they have three dimensions, such as length, breadth, and height, solids are three-dimensional forms. Solids are the bodies that occupy space.
Terms of Solid Geometry:
Point: Point has no dimension, it has position only.
Line: A line has only length. It refers to one dimension.
Surface: A surface contains length and breadth, and it has two dimensions.
Solid: A solid has all such as length, breadth, and thickness or height.
For example, the book is known as solid geometric because it contains 6 faces such as a surface; each of its edges is called a line and each corner is considered a point.

Book
The following are a few illustrations of solid or three-dimensional shapes:
Cubes: A cube is a 3-D object. six-sided solid form with six faces. One of the most basic forms in three dimensions is the cube. A cube's six faces are all squares, making it a two-dimensional object.
Cuboids: A solid with six rectangular faces that are perpendicular to one another.
Rectangular Solids: A quadrilateral with parallel sides that are equal to one another and four equal vertices is known as a rectangle.
Prism: A prism is a solid object with flat sides or surfaces, a uniform cross-section throughout its length, and two identical ends (such as a triangle, square, rectangle, etc.).
Cylinders: A cylinder is a three-dimensional solid object with two bases that are identically circular and are connected by a curving surface that is located at a certain height from the centre.
Spheres: A sphere is a three-dimensional object that is round in shape.
Cones: A cone is a three-dimensional geometric structure with a smooth transition from a flat, generally circular base to the vertex, a point that creates an axis to the base's centre.
Pyramids: A three-dimensional form is a pyramid. A pyramid's flat triangular sides unite at a common point known as the apex and have a polygonal base.
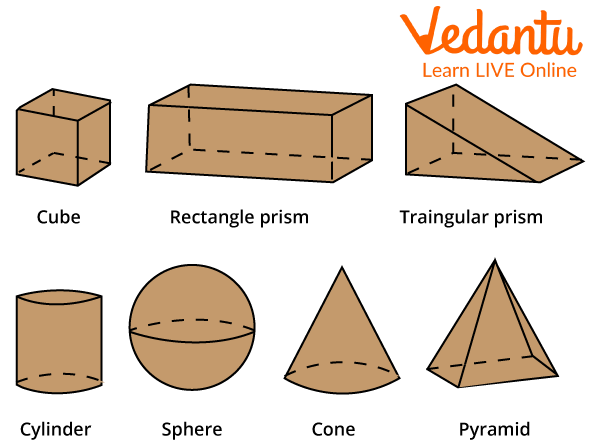
Examples of Geometric Shapes
A Geometric Solid has Only Length and Height:
In solid geometry, shapes contain length, breadth, and height. But there are few shapes that we can consider geometric solids with only length and height. Here, the cone, sphere, and cylinder are also known as solid shapes in geometry. These shapes contain only length and height. In cone or cylinder shapes, there are only lengths, radii, and heights.
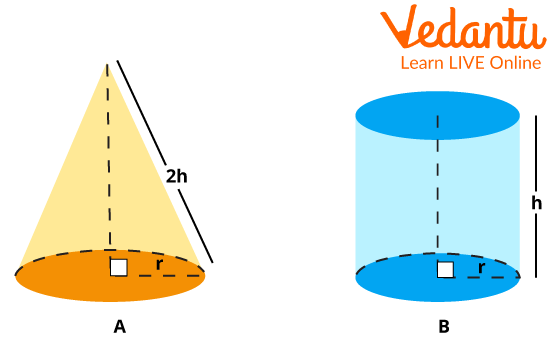
Length and Height of a Figure
In a sphere shape, there will be only one radius, which is used as length or height. The reason for this is that because the sphere is round, it does not have the same height and length as other shapes. So to calculate the area, perimeter, etc., of the sphere, only the radius measurement is used. As we can see in the image below, we can only use the radius and diameter as measurements.
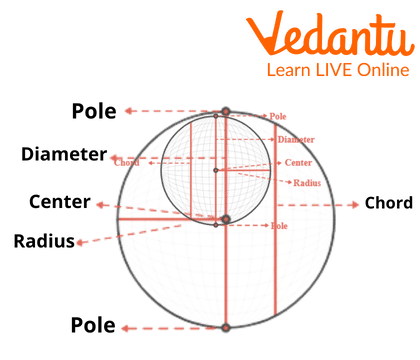
Sphere
Solid Geometry Graph Line:
A graph line is a type of chart used to show some information. Here we study geometrical shapes in graphs. When we represent solid space in.
Solid Geometry Graph Line
In graphs, we can usually represent the 3 axes in each graph as x, y, and z in three-dimensional space for solid geometry. The geometry is shown in the graph to demonstrate all three angles, as we have already discussed that the solid is three-dimensional, and to make it clearer and easier to understand. Solid geometry is useful in graphs.
Solved Examples:
1. Define the total faces and lines in a pyramid.
Ans: Faces in Pyramids = 5
Lines in a pyramid = 8
2. What are the faces, lines, and points in a Cuboid?
Ans: Faces in Cuboid = 6
Lines in Cuboid = 12
Points in Cuboid = 8
3. Match the following:
Ans:
Conclusion:
It may be said that solid geometry permeates every aspect of daily existence. Everywhere is a closed, three-dimensional space. Solid geometry enables us to investigate novel ideas about the forms or figures that we may observe. A solid form is essentially a 3D object, such as a cube, cuboid, cone, etc. We can determine its volume, surface area, and more. In the upcoming section, we will solve and understand the question related to solid geometry.
FAQs on 3D - Geometry(Solid Geometry)
1. What is 3D Geometry, and why is it also called Solid Geometry?
3D Geometry, or Three-Dimensional Geometry, is a branch of mathematics that deals with shapes and figures in a three-dimensional space. It is often called Solid Geometry because it focuses on objects that have length, width, and height, such as cubes, spheres, and cylinders. Unlike plane geometry which studies flat shapes, solid geometry explores the properties and relationships of these solid figures.
2. How does 3D Geometry fundamentally differ from Plane Geometry?
The fundamental difference lies in the number of dimensions. Plane Geometry (2D) operates on a flat plane using two dimensions (length and width) and deals with shapes like lines, circles, and polygons. 3D Geometry adds a third dimension (height or depth), allowing for the study of solid shapes and their position in space using a coordinate system with x, y, and z-axes.
3. What are Direction Cosines (DCs) and Direction Ratios (DRs) in 3D Geometry?
Direction Cosines and Direction Ratios are crucial for defining the orientation of a line in 3D space.
- Direction Cosines (l, m, n) are the cosines of the angles (α, β, γ) that a line makes with the positive x, y, and z-axes, respectively. A key property is that l² + m² + n² = 1.
- Direction Ratios (a, b, c) are any set of three numbers that are proportional to the Direction Cosines. They provide the direction of the line but not its specific angles with the axes.
4. What is the conceptual difference between skew lines and parallel lines in 3D space?
This is a concept unique to 3D geometry. Parallel lines lie in the same plane and never intersect, maintaining a constant distance apart. In contrast, skew lines are lines that do not lie in the same plane, are not parallel, and never intersect. Imagine one flyover bridge passing directly above a road below it; the paths they represent are skew.
5. Why are Direction Cosines essential for defining a line's orientation in space?
In 3D space, a single angle or slope is insufficient to describe a line's tilt. Direction Cosines are essential because they provide a unique and standardized set of three values that precisely fix the line's orientation relative to all three coordinate axes. This allows for unambiguous calculations of angles between lines and the relationship between lines and planes, forming the bedrock of analytical 3D geometry.
6. How is the equation of a line represented in 3D Geometry as per the CBSE syllabus?
According to the CBSE 2025-26 syllabus, the equation of a line in 3D space can be represented in two primary forms:
- Vector Form: r = a + λb, where 'a' is the position vector of a point on the line and 'b' is a vector parallel to the line.
- Cartesian Form: (x - x₁) / a = (y - y₁) / b = (z - z₁) / c, where (x₁, y₁, z₁) is a point on the line and (a, b, c) are the direction ratios of the line.
7. How is a plane defined in three-dimensional geometry?
A plane is a flat, two-dimensional surface that extends infinitely in 3D space. Analytically, it is defined by its normal vector—a vector that is perpendicular to the plane—and a known point that lies on the plane. The general equation of a plane in Cartesian form is Ax + By + Cz + D = 0, where A, B, and C are the direction ratios of the normal vector.
8. What are the real-world applications of 3D Geometry?
3D Geometry is critical in many advanced fields. Its applications include:
- Architecture and Engineering: For designing buildings, bridges, and complex structures using CAD software.
- Computer Graphics: In creating realistic 3D models for video games, movies (CGI), and virtual reality.
- Medical Imaging: For constructing 3D models from CT scans and MRIs to help in diagnosis and surgery.
- Astronomy and Navigation: To calculate the positions and trajectories of satellites, planets, and spacecraft.
9. How can we find the shortest distance between two skew lines?
The shortest distance between two skew lines is the length of the line segment that is perpendicular to both lines. The formula, crucial in the Class 12 syllabus, is derived using vector algebra. If the lines are given by r₁ = a₁ + λb₁ and r₂ = a₂ + μb₂, the shortest distance (d) is calculated as the projection of the vector connecting the two lines (a₂ - a₁) onto the direction of their common perpendicular (b₁ x b₂). The formula is: d = |(a₂ - a₁) ⋅ (b₁ x b₂)| / |b₁ x b₂|.















