




What is a Set?
Set definition: Each set is defined as a group of various items sharing some common trait among themselves. Set members or elements refer to the items that comprise a set. Examples of sets include a collection of cards, a group of automobiles, a group of birds, a group of days of the week, etc. Also, there exist some universally accepted sets like the set of natural numbers, the set of rational numbers, the set of real numbers, the set of integers, the set of whole numbers, the set of irrational numbers, etc.
What is the Cardinality of Sets?
The cardinality of a set is the measure of the size of the set, indicating the number of items contained in that set. It can have both finite and infinite values. The cardinality of the set A = (1, 2, 3, 4, 5, 6) is equal to 6 as set A encompasses six items. Often the cardinality of any set is referred to by the modulus sign appearing on both sides of the set name, for example, |A|.
What are the Methods of Representation of Sets?
Irrespective of the way of representation, every set is named with a capital or an uppercase English alphabet. The set names can be represented, for instance, with the letters A, B, C, D, etc. Small hand or lowercase English alphabets or numeric and other symbols represent the constituent members or the elements of sets. For instance, A = {11, 12, 13, 14, 15}, B={x: x a,c,r,t,f,h,j}
Set representations can be of the following three forms.
Set Builder Form for Representation of Sets
A definite way of describing a set making use of a single element and the statements that illustrate the characteristics of its components, separated by the symbol “:”.
To indicate whether an element is present in the given set or not, we use the Greek letter aphsilon "" . It indicates the phrase “belongs to”.
Again the symbol “∉” is interpreted as "not belonging to."
For example $A=\{x:x\text{ }is\text{ }an\text{ }even\text{ }number,\text{ }x\in N\text{ }and\text{ }x\le 25\}$
Therefore, the set A consists of the elements given by A= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}.
Roster Form for Representation of Sets
Roster form representation refers to the method of expressing a set where the elements of the sets are discretely shown and enclosed within curly braces. The tabular form is another name for this type of set representation.
For example, N= {1,2,3,4,5,6,7,8,9,10,........}
Statement Form for Representation of Sets
Statement form representation refers to the method of denoting a set where the elements of the sets are never discretely shown, but onlt the statement is enclosed within curly braces.
For example, N= {the natural numbers}
What are the Different Types of Sets?
Some of the noteworthy various type so f sets are as follows:
Null set
This defined set contains no elements in it, and hence, is also called an empty set.
Universal Set
A set which contains all the sets defined in a mathematical statemement or problem.
Finite Set
The set whose cardinality is finite.
Infinite Set
The set whose cardinality is infinite.
Superset
By comparing any two sets A and B, if we find every element of the set B is present in set A but every element of set A is not present in the set B, we say that B is a superset of A.
Subset
By comparing any two sets A and B, if we find every element of the set B is present in the set A, we say that B is a subset of A.
Equivalent Set
By comparing any two sets A and B, if we find every element of the set B is present in the set A and vice versa, we say that B is an equivalent set of A and vice versa.
Common Sets of Numbers
The following notations can be used to represent the number sets:
N = Set of Natural numbers
W = Set of Whole numbers
R = Set of real numbers
Q = Set of Rational numbers
Z = Set of Integers
T = Set of Irrational Numbers
What is the Union of Sets?
The union of any two sets namely set P and set Q indicates the elements that are present in either of the sets P and Q. It is indicated symbolically by the statement $P\cup B$.
What is the Intersection of Sets?
The intersection of any two sets, namely set P and set Q indicates the elements that are present in both the sets P and Q. It is indicated symbolically by the statement $P\cap B$
What is a Venn Diagram?
Visual diagrams may be used to depict sets as well. A Venn diagram is the visual representation of a set. In a Venn diagram, the sets are represented graphically or visually as circles, and the intersection of the circles reveals each set's connection. The rectangular region around the sets or circles is referred to as the universal set, while the area inside the circles, or the sets, is referred to as the elements.

Venn diagram representing two sets
There are two sets A and B that overlap one another, as seen in the image above. The items shared by the two sets supplied are shown in this intersection. The universal set, denoted by the letter U, which symbolises all the items that may or may not be present in the sets, is the rectangular area around the sets.
Solved Examples
1. Write the following set statement in both set-builder form and roster form. Set of all natural numbers that lie between 1 and 40 that are prime.
Ans. the above set statement can be represented in following ways:
Set-builder form: A=x| x is prime, 1x40 and xN
Roster form: A=2,3,5,7,11,13,17,19,23,29,31,37
2. Draw the venn diagram for the following:
In a college, 200 students are selected. 120 like tea, 140 like coffee and 50 like both tea and coffee.
Ans. Let T = set of students who like tea
C= set of students who like coffee
n(T) = Cardinality of set T
= 120
n(C) = Cardinality of set C
= 140
n(T\[\cap\]C) = cardinality of students who like both tea and coffee
= 50
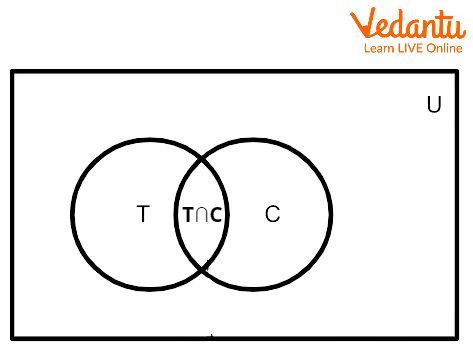
Students who like both tea and coffee
3. Write the set builder Form for A={2,3,4,5,6,7,8,9}
Ans. A={x| x is a natural number and 2x9}
4. Write the following set statement in set-builder form. Set of all whole numbers less than 20 that are composite.
Ans. The above set statement can be represented in following ways:
Set-builder form: $A=\{x:x\text{ }is\text{ }composite,\text{ }0\le x\le 20\text{ }and\text{ }x\in W\}$
5. Write the following set statement in roster form. Set of all whole numbers less than 20 that are composite.
Ans. The above-set statement can be represented in the following ways:
Roster form: $A=A=4, 6,8,9,10,12,14,15,16,18,20$
Summary
The sets represent the statements that can define the relationship among the elements given in a group.
The sets can be displayed in three ways: set-builder, statement form and roster form.
The cardinality of sets indicates the number of elements in a set, which can be infinite or finite.
The visual representation of sets makes use of Venn diagrams to show the correct relationship among the sets.
Practice Problems
Q1. Write the following set statement in both set-builder form and roster form. Set of all even prime numbers.
Q2. Write the following set statement in both set-builder form and roster form. Set of all odd prime numbers less than 100.
Q3. Write the following set statement in both set-builder form and roster form. Set of all even composite numbers between 200 and 300.
List of Related Articles
FAQs on Sets and Their Representation
1. What exactly is a set in mathematics?
In mathematics, a set is a well-defined collection of distinct objects. The term 'well-defined' means that we should be able to tell with certainty whether a particular object belongs to the set or not. For example, the collection of all vowels in the English alphabet is a set, as it contains the specific elements a, e, i, o, u.
2. What are the two main ways to represent a set?
There are two primary methods for representing a set as per the NCERT syllabus:
- Roster or Tabular Form: In this method, all the elements of the set are listed, separated by commas, and enclosed within braces { }. For example, the set of even numbers less than 10 is {2, 4, 6, 8}.
- Set-Builder Form: In this method, we write a rule or a property that all elements of the set must satisfy. For example, the same set can be written as {x : x is an even natural number less than 10}.
3. What are the most common types of sets I need to know for my exams?
For Class 11, you should be familiar with several key types of sets:
- Empty Set (∅ or {}): A set containing no elements.
- Finite and Infinite Sets: Sets with a limited number of elements are finite, while those with an unlimited number are infinite.
- Singleton Set: A set that has only one element.
- Subsets (⊆): Set A is a subset of set B if all elements of A are also in B.
- Equal Sets: Two sets are equal if they have exactly the same elements.
- Power Set: The collection of all possible subsets of a set.
- Universal Set (U): A larger set that contains all the elements being considered in a particular context.
4. What is the practical importance of learning about sets?
Understanding sets is fundamental because it is the basic building block for many other areas of mathematics and computer science. It helps in:
- Organising and structuring data logically.
- Understanding databases and search algorithms in computer science.
- Forming the foundation for more advanced topics like Relations, Functions, and Probability.
- Developing logical thinking and problem-solving skills.
5. What is the real difference between a subset (⊆) and a proper subset (⊂)?
This is a common point of confusion. The main difference is whether the sets can be equal.
- A subset (⊆) means that every element of the first set is also in the second set. The first set can be smaller than or equal to the second set.
- A proper subset (⊂) means the first set is strictly smaller than the second. It must have at least one fewer element.
For example, if A = {1, 2}, then {1} is a proper subset of A, and {1, 2} is a subset of A, but not a proper subset.
6. How does the formula for the union of two sets change if they have no common elements?
The general formula for the union of two sets X and Y is n(X ∪ Y) = n(X) + n(Y) - n(X ∩ Y). If the sets have no common elements, they are called disjoint sets. In this case, their intersection (X ∩ Y) is the empty set, meaning n(X ∩ Y) = 0. So, the formula simplifies to just n(X ∪ Y) = n(X) + n(Y).
7. How is a 'Power Set' constructed and what does it represent?
A Power Set of any set 'A', shown as P(A), is the set containing all possible subsets of A. To construct it, you list every single combination of elements from A, including the empty set (∅) and the set A itself. For instance, if A = {1, 2}, its Power Set is P(A) = {∅, {1}, {2}, {1, 2}}. It represents the entire family of subsets related to the original set.
8. Why is the empty set (∅) considered a subset of every set?
This is a rule based on logic. A set 'A' is a subset of 'B' if there are no elements in 'A' that are not also in 'B'. Since the empty set has no elements at all, this condition can never be broken. There are no elements in ∅ to be 'not in' any other set, so it is logically considered a subset of every set, including itself.









