




Introduction to Projection
Our lives are made more ordered and less confusing by mathematics. Power of reasoning, creativity, logical thinking, critical thinking, problem-solving abilities, and even excellent communication skills are some of the attributes that mathematics generates.
It is believed that shadows produced by objects on the ground are where the concept of projection in mathematics first emerged. A geometric projection is like a shadow that an object casts onto another object. When a three-dimensional sphere is projected onto a plane, its projection will be a circle or an ellipse. In this article, we will learn about the projection of a sphere onto the plane.
What is Projection?

Projection Using Figures
Geometric projection is the area of geometry that deals with the characteristics and rules of geometric shapes when they are projected. By linking corresponding points on the two planes with parallel lines, a projection is the conversion of points and lines in one plane onto another. This can be seen as creating an image of whatever is drawn on one sheet of paper on another by shining a (point) light source (placed at infinity) through the translucent sheet of paper.
Projection Example in Real Life
Camera: The projective plane is extremely useful in image registration, especially in camera resectioning. To convert a 3D camera image into a 2D one, we need to convert it from 3D space to 2D space. By using projective geometry, this transformation can be described as a linear mapping from 4D to 3D.
Computer: In computer vision, projective geometry is widely used to transform a photograph (a 2D perspective view of a 3D world) into a projective transformation. Therefore, due to their projective limitations, planar images can only provide limited geographic information.
Projection of a Sphere onto the Plane
A mathematical method called sphere projection. Let us visualise the sphere's points on the plane.
There are many different projection types, and because the sphere and the plane are not locally identical, these projections are affected to different degrees. One selects a suitable projection type, considering its characteristics, depending on the goal.
Example: Globe Map on a Plane sheet
The Projection of the Content of a Spherical Globe on a Plane Surface
The magnitude of the area of a region on the map is identical to the area of the same region depicted on the sphere, which is an example of a map that maintains areas. The projection, however, is not uniform.
When two curves intersect at a single point and form an angle, their projections cross at that same point and form an angle with the same magnitude. When a projection possesses this property, it is said to be symmetric.
Map Projection Facts

Miller Cylindrical Projection
Miller's cylindrical projection is used to depict a cylinder on the globe.
Despite being oriented around a different axis, this transverse Mercator projection is mathematically equivalent to a normal map.
A sinusoidal projection depicts relative sizes accurately but severely distorts forms. The map can be "disrupted," reducing distortion.
Shapes and sizes are distorted elsewhere, while distances and directions from the central point are precisely depicted.
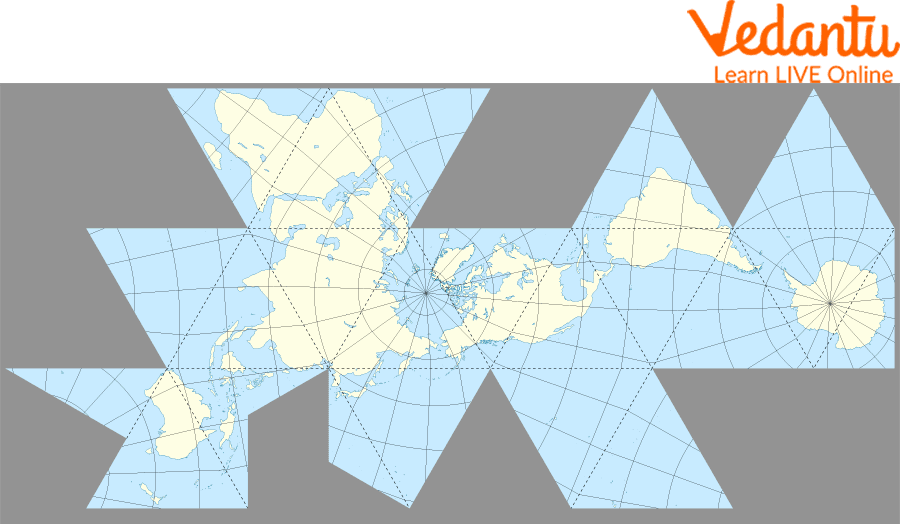
Dymaxion Map by Buckminster Fuller
This is how the Dymaxion map by Buckminster Fuller looked. While conformal and perspective, a stereographic projection is neither equal-area nor equidistant.
Thales created the Gnomonic projection in the sixth century BC, regarded as the oldest map projection.
Summary
Projective geometry makes understanding some geometric objects easier by neglecting measurements like distances and angles. Since then, many more complex fields have adopted these insights. Because capturing a photograph (a 2D perspective view of a 3D world) corresponds to a projective transformation, computer vision is widely employed. In a sphere, the term "projected area" refers to measuring a three-dimensional object's area in two dimensions.
FAQs on Projection
1. What is meant by the projection of a vector in mathematics?
In vector algebra, the projection of one vector onto another non-zero vector is essentially its shadow or component in the direction of the second vector. Imagine a light source shining perpendicularly onto the line containing vector b; the shadow cast by vector a is its projection onto b. This concept is fundamental in understanding vector components and is used in both scalar and vector forms.
2. What is the formula to calculate the projection of a vector 'a' onto another vector 'b'?
The calculation depends on whether you need the scalar or vector projection. As per the CBSE/NCERT syllabus, the formulas are:
- Scalar Projection (the length of the shadow): This is a magnitude, calculated as (a ⋅ b) / |b|.
- Vector Projection (the shadow itself as a vector): This has both magnitude and direction, calculated as ((a ⋅ b) / |b|²) * b.
3. What is the key difference between scalar projection and vector projection?
The primary difference lies in the nature of the result:
- A scalar projection is a number that represents the length or magnitude of the projection. It can be positive or negative, indicating direction relative to the base vector.
- A vector projection is a vector itself. It has both the magnitude (from the scalar projection) and the direction of the vector it is projected onto.
Essentially, scalar projection answers 'how long is the shadow?', while vector projection answers 'what is the shadow vector?'.
4. How is the concept of vector projection applied in Physics?
Vector projection is crucial for solving many problems in physics. One of the most common applications is in calculating Work Done. Work is the dot product of the Force and Displacement vectors (W = F ⋅ d). This calculation inherently uses the projection of the force vector onto the displacement vector to find the component of force that actually contributes to the work.
5. What happens to the projection of vector 'a' onto 'b' if the two vectors are perpendicular (orthogonal)?
If two vectors a and b are perpendicular, their dot product (a ⋅ b) is zero, because the angle between them is 90° and cos(90°) = 0. Consequently, both the scalar and vector projections of a onto b will be zero. Geometrically, this makes sense as a vector casts no shadow on a line that is perpendicular to it.
6. Can the scalar projection of a vector be negative, and what would that signify?
Yes, a scalar projection can be negative. This occurs when the angle (θ) between the two vectors is obtuse (i.e., 90° < θ ≤ 180°). Since cos(θ) is negative in this range, the dot product becomes negative. A negative scalar projection signifies that the projection vector points in the exact opposite direction to the base vector it is being projected onto.
7. Why is the dot product used to find vector projection?
The dot product is used because its definition, a ⋅ b = |a| |b| cos(θ), naturally contains the term for an adjacent side of a right-angled triangle. The term |a| cos(θ) represents the length of the projection of vector a onto vector b. Therefore, dividing the dot product by the magnitude of b isolates this projection length, making it a direct and efficient method for the calculation.




























