




How Does Each Digit Hold a Value in Any Given Number?
Your mom is still a mom whether she is in the kitchen, garden, living room, or the basement. But digits like 5 at different places (for example, tens or hundreds of places) means something different. Every digit in a number has a place value in Mathematics. Place value is the value represented by a digit in a number based on its place in the number. In this article we'll help you out to understand it in an easy way.
Place value for Grade 4 is important because it serves as a foundation for grouping, multiple-digit multiplication, and other operations in the decimal system, as well as a starting point for learning about other base systems. By understanding this you'll be able to understand the key differences like Rs. 50 you got for your birthday and the Rs. 500 price tag on the Remote Car for which you're saving for.
In Mathematics, the position or place of a digit in a number is referred to as place value. Each digit has a specific place in a number. The position of each digit will be expanded when we represent the number in general form. Those positions begin with a unit position, often known as one's position. Units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on are the place values of a number's digits in sequence from right to left.
What Is Place Value?
The value of each digit in a number is determined by its position in that number. We have given a chart below, that is a place value chart which helps in the identification of large numbers. This place value chart is read from left to right. In the Indian system, we begin arranging numbers from right to left in groups of three, and then in groups of two. The place value chart is divided into intervals, which include ones, thousands, lakhs, and crores.
The 5 in 250, for example, indicates 5 tens, or 50; whereas, the 5 in 5,126 denotes 5 thousands, or 5,000. It is important to understand that while a digit can be the same, its value is determined by its position in the number. A place value grid, such as the one shown below, will most likely be used to understand place value in a better way.

Place value chart
International Place Value Chart
The International place value chart is a place value system that is used in many countries around the world. We use a place value chart to understand the place value of each digit so that we can identify each digit. We start grouping the numbers from right to left in groups of three, called periods, and we place a comma or space after each period to make the number easier to read.
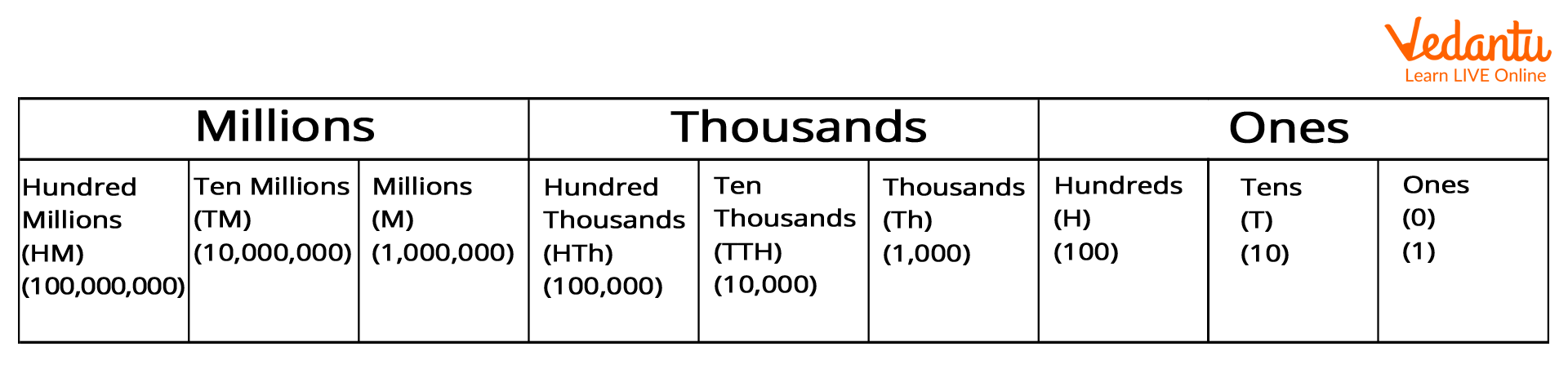
International place value chart
Place, Place Value and Face Value
A number is made by grouping a few digits together.
Each digit will have a fixed position called its place.
Each digit’s value depends on its place, which is known as the place value of the digit.
The face value of a digit in the given number is just the value of the digit itself.
The place value formula of a digit can be written as the product of face value of the digit and value of the place.
That is,
Place value = (Face value of the digit) × (Value of the place)
Example:
In the number 874321, write the digit which is in:
(a) hundreds place
(b) hundred thousand place
(c) ten thousand’s place
(d) and One’s place
Sol:
(a) A number in hundreds places is 3.
(b) A number in a hundred thousand places is 8.
(c) A number in ten thousand’s place is 7.
(d) The number in One’s place is 1.
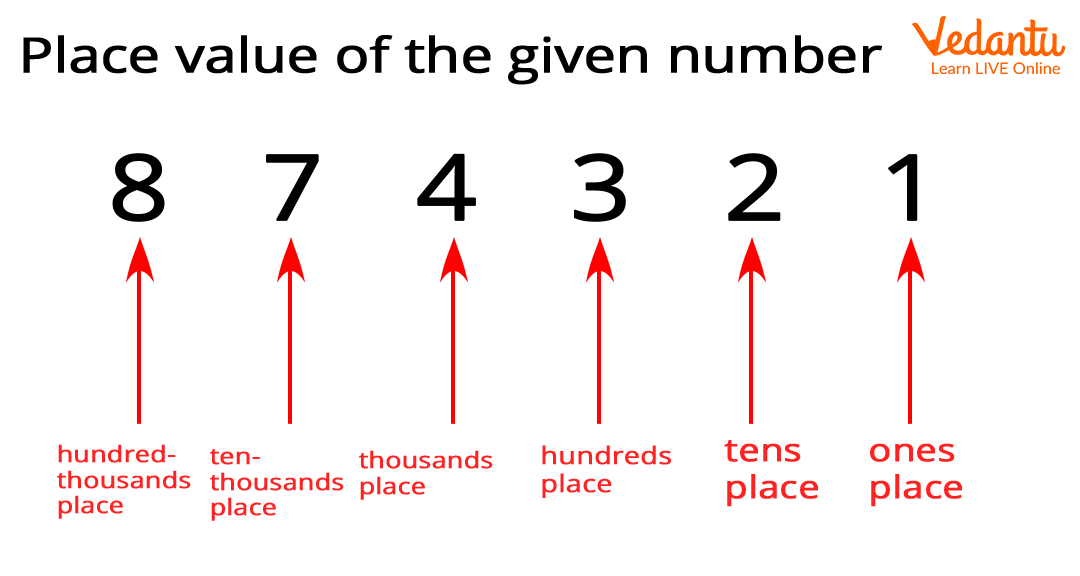
Place values of each digit in the number 874321
Conclusion
Having a strong understanding of place value is a good step because it gives you the key number knowledge you need to solve calculations like addition, subtraction, multiplication, division, and fractions. It would be difficult to write numbers, identify one more or one less, count forwards and backwards, or compare numbers if you are not thorough about place value. Moreover, understanding place value in Maths has a significant impact on how we think about basic concepts such as money. Understanding place value can help you figure out how much something costs when we wish to buy it.
FAQs on Understanding Place Value in the Number System
1. What is meant by place value in the number system?
Place value is the value a digit holds based on its specific position in a number. In the Indian and International number systems, each position (like ones, tens, hundreds, thousands) has a unique value. For example, in the number 542, the digit '5' is in the hundreds place, so its place value is 500.
2. What is the key difference between the place value and face value of a digit?
The main difference lies in how a digit's value is determined:
- Face Value: This is the digit's actual, inherent value, regardless of its position. In the number 789, the face value of '8' is simply 8.
- Place Value: This is the value a digit gets due to its position in the number. In 789, the digit '8' is in the tens place, so its place value is 80 (8 x 10).
3. How can you determine the place value of a specific digit in a large number?
To find the place value of a digit, you multiply the digit's face value by the value of its position in the number. For example, to find the place value of '6' in the number 9,64,321:
1. Identify the digit: 6.
2. Determine its position: It is in the 'lakhs' place.
3. Calculate the place value: 6 × 1,00,000 = 6,00,000. Thus, the place value of 6 is six lakh.
4. How do you write a number in its expanded form using place values?
Writing a number in its expanded form means expressing it as the sum of the place values of all its digits. For instance, the expanded form of 3,458 is written as:
3000 + 400 + 50 + 8
This shows that the number is made up of 3 thousands, 4 hundreds, 5 tens, and 8 ones.
5. How does a place value chart help in understanding and comparing numbers?
A place value chart is a table that visually organizes digits according to their positions (Ones, Tens, Hundreds, etc.). It helps students in two major ways:
- Understanding: It clearly shows how the value of a digit increases as it moves to the left, making large numbers easier to read and comprehend.
- Comparing: To compare two numbers, you can place them in the chart and compare the digits starting from the leftmost position. The number with the larger digit in the highest place value position is the greater number.
6. Why is a strong understanding of place value considered essential for learning advanced mathematics?
Understanding place value is the foundation of the entire number system. Without it, students struggle with more complex operations. A strong grasp of place value is crucial for:
- Arithmetic Operations: Correctly aligning numbers for addition, subtraction, multiplication, and division.
- Decimals and Fractions: Understanding the value of digits after the decimal point.
- Number Sense: Developing an intuitive feel for number magnitude, estimation, and rounding.
- Algebra: Understanding polynomials and variable coefficients builds on the same positional value concept.
7. How does the concept of place value apply to decimal numbers?
The concept of place value extends to the right of the decimal point, representing parts of a whole number. While positions to the left of the decimal increase by powers of 10 (tens, hundreds), positions to the right decrease by powers of 10. These positions are called tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on. For example, in 24.35, the '3' has a place value of 3/10, and the '5' has a place value of 5/100.
8. Beyond school maths, what are some real-world examples where place value is important?
Place value is used constantly in everyday life, often without us realising it. Key examples include:
- Handling Money: Differentiating between ₹5.00, ₹50, and ₹500 is a direct application of place value. A misplaced zero can make a huge difference.
- Measurement: Reading measurements of length (metres and centimetres), weight (kilograms and grams), or volume (litres and millilitres) depends on understanding decimal place value.
- Technology and Data: Understanding large numbers, like file sizes (KB, MB, GB) or population statistics, requires a solid grasp of the place value system to comprehend their scale.









