




How Do Decimals Work? Key Rules and Real-World Uses
On a number line, decimals are a set of numbers that lie between integers. They are simply another way to represent fractions. We can write more precise values of measurable quantities such as length, weight, distance, money, etc using decimals.
The numbers to the left of the decimal point are integers or whole numbers, while the numbers to the right are decimal fractions. In this article, we will learn about decimals.
Decimals Number System
The decimal number system is a positional notation that has a base of 10. It refers to numbers with a fractional part separated from an integer part by a decimal separator. Decimals allow us to write fractions without having to write a fraction with a numerator and denominator.

The above image Illustrates the Parts of a Decimal Number
Decimal Place Value Chart
The position of each digit is important when writing any number. When we go to the right in the below place value chart, the value of the digit becomes 10 times smaller, i.e., one-tenth, and when we move to the left, the value of the digit becomes ten times larger.
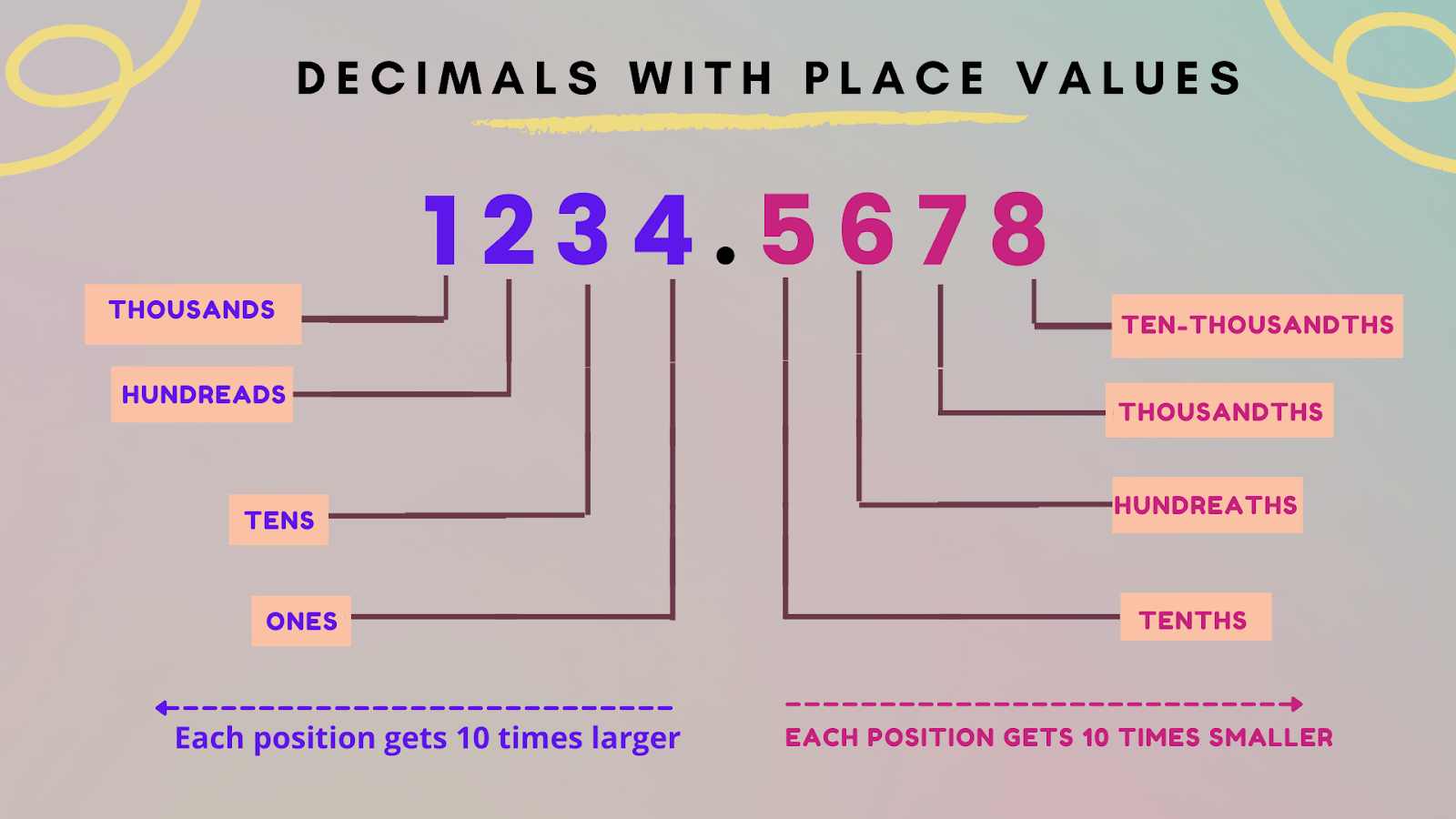
The above Decimals images Illustrate a Decimal Number with Corresponding Place Values
Types of Decimals
Decimals are categorised based on the type of digits that follow the decimal point. It depends on whether the digits are non-terminating or terminating.
Examples:
Non-terminating: 122.353535.... , 3.33333...., 13.66666…
Terminating: 85.9856, 2.5674, 7.5
Conclusion
The decimal numeral system is a standard system for showing integer and non-integer numbers. You can't learn about numbers completely unless you understand decimals. Hopefully, this article has offered you a good understanding of the significance of decimals.
To learn more mathematical concepts, explore our website.
FAQs on Decimal Number System Explained for Students
1. What are decimals and where do we encounter them in our daily lives?
Decimals represent numbers that have a whole part and a fractional part, separated by a decimal point. They are essentially a way to write fractions using a base-ten system. We use them frequently in everyday situations, such as:
- Money: Prices like ₹99.50 or ₹125.75.
- Measurements: A person's height (e.g., 152.5 cm), weight (e.g., 55.8 kg), or temperature (e.g., 98.6°F).
- Sports: Recording race times down to a fraction of a second, like 9.58 seconds.
2. How does the decimal point function in a number?
The decimal point is a crucial symbol that separates the whole number part (on its left) from the fractional or partial number part (on its right). Every digit to the left of the point has a value of one or more, while every digit to the right has a value that is less than one.
3. What is the correct way to read a decimal number, for example, 36.45?
To read a decimal number correctly, you should:
- Read the whole number part as usual (e.g., "thirty-six").
- Say the word "point" for the decimal point.
- Read each digit after the decimal point individually.
So, 36.45 is read as "thirty-six point four five," not "thirty-six point forty-five."
4. How can you compare two decimal numbers, like 8.62 and 8.7?
To compare decimals, you can follow these steps:
- Step 1: Compare the whole number parts (the digits to the left of the decimal). If they are different, the larger whole number makes the larger decimal.
- Step 2: If the whole numbers are the same, compare the digits in the tenths place (the first digit after the decimal).
- Step 3: If the tenths are also the same, move to the hundredths place, and so on.
For 8.62 and 8.7, the whole number part (8) is the same. Comparing the tenths place, 7 is greater than 6. Therefore, 8.7 is greater than 8.62.
5. How do you convert a fraction into its decimal form?
The most direct method to convert any fraction into a decimal is to divide the numerator by the denominator. For example, to convert the fraction 3/4 into a decimal, you would perform the division 3 ÷ 4, which results in 0.75. For fractions that have a denominator of 10, 100, or 1000, you can simply write the numerator and place the decimal point accordingly (e.g., 27/100 = 0.27).
6. How can a decimal number be converted back into a fraction?
To convert a decimal to a fraction, you first write the decimal digits as the numerator and use a power of 10 (10, 100, 1000, etc.) as the denominator, based on the number of decimal places. For instance, 0.85 has two decimal places, so it becomes 85/100. The final step is to simplify the fraction to its lowest terms. In this case, both 85 and 100 are divisible by 5, so the simplest form is 17/20.
7. What do the place values like tenths, hundredths, and thousandths mean after a decimal point?
These place values represent fractions with a denominator of 10, 100, 1000, and so on. The position of a digit after the decimal point determines its value:
- The first digit is in the tenths place (representing a fraction over 10).
- The second digit is in the hundredths place (representing a fraction over 100).
- The third digit is in the thousandths place (representing a fraction over 1000).
For example, in the decimal 0.125, the '1' represents 1/10, the '2' represents 2/100, and the '5' represents 5/1000.
8. Why does adding zeros to the end of a decimal (e.g., changing 0.5 to 0.50) not change its value?
Adding zeros to the end of a decimal does not change its value because it is like creating an equivalent fraction. The decimal 0.5 is the same as the fraction 5/10. When you change it to 0.50, its fractional form becomes 50/100. Since 5/10 and 50/100 are equivalent fractions (you can get 50/100 by multiplying the numerator and denominator of 5/10 by 10), the actual value remains unchanged.
9. What is the main difference between a decimal and a fraction?
While both represent parts of a whole, the main difference lies in their format and the denominators they can have. A fraction can have any whole number as its denominator (e.g., 3/7). A decimal is a special kind of fraction where the denominator is always a power of ten (like 10, 100, or 1000), which is implicitly shown by the position of the decimal point.
10. What is a common mistake to avoid when adding or subtracting decimals?
The most common mistake students make is not aligning the decimal points correctly before starting the calculation. When adding or subtracting, you must line up the numbers vertically so that all the decimal points are in a straight column. This ensures that you are adding or subtracting corresponding place values (tenths with tenths, hundredths with hundredths, etc.).















