




Introduction to Perimeter of Quadrilateral
Do you see some four-sided objects around you like books, papers, walls, floor, kite, doors, etc.? Do you know the common factor in all of these things? In Geometry, a plane shape with four sides or edges and four corners or vertices is called a quadrilateral. The sum of internal angles of a quadrilateral is 360 degrees. The length of a quadrilateral's boundary as a whole is its perimeter. An irregular or regular four-sided polygon is also referred to as a quadrilateral.
After reading this article, one can answer questions like what is the perimeter of a quadrilateral, how to find the perimeter of a quadrilateral, etc.

Introduction to a Quadrilateral
What is the Perimeter of a Quadrilateral?
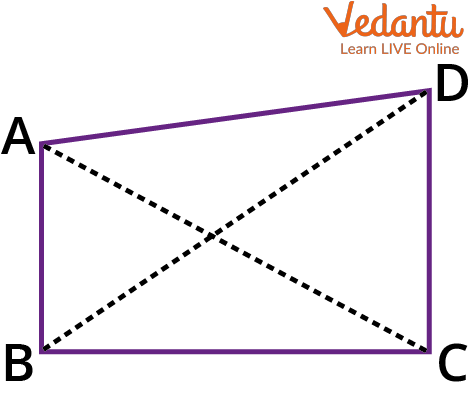
What is the Perimeter of a Quadrilateral?
The total length around any two-dimensional shape is called its perimeter.
For example: In the above quadrilateral, the perimeter of the quadrilateral is
ABCD = AB + BC + CD + AD
To find the perimeter of any plane shape, add the length of all the sides. The quadrilateral has four sides. So, add the lengths of four sides to get the perimeter.
How to Find the Perimeter of a Quadrilateral?
To find the perimeter of a quadrilateral, we need to add all the lengths of four sides, i.e., the perimeter of ABCD Quadrilateral = sum of lengths of all sides = AB +BC + CD + DA.
In other words, if we join all four sides of a quadrilateral such that it forms a line segment, the length of the resultant line segment is called a perimeter. The unit of the perimeter in the S.I system is ‘metre (m)’, and in the CGS system is ‘cm’.
The Perimeter of Quadrilateral Formula
The following are the perimeter of the quadrilateral formulas or the perimeter equation of quadrilaterals.
Square
A Square
To find the perimeter of the square,
Perimeter of square $A B C D=A B+B C+C D+A D$
As lengths of all sides are equal, i.e. $A B=B C=C D=A D$
Perimeter $=4 \times A B=4 \times$ Length of any side.
Rectangle
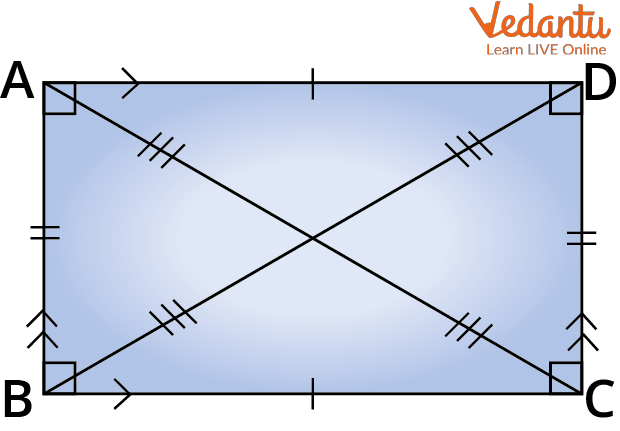
A Rectangle
Perimeter of rectangle = AB + BC + CD + AD
As lengths of opposite sides are equal i.e AB = CD = length and BC = AD = breadth
We get, Perimeter of rectangle $=2 \times(A B+B C)$
$=2 \times(C D+A D)$
$=2 \times$ (length + breadth)
Parallelogram
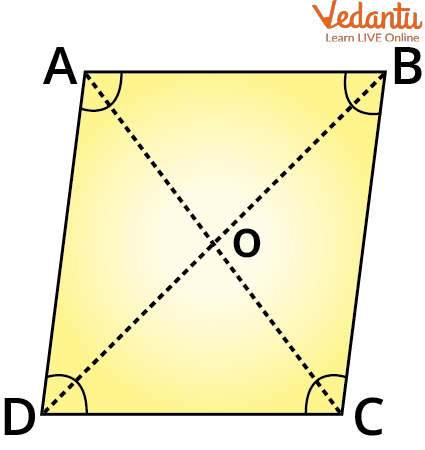
A Parallelogram
Perimeter of parallelogram = AB +BC +CD +AD
As lengths of opposite sides are equal i.e., AB =CD= a and BC=AD= b
We get, parallelogram $=2 \times(\mathrm{AB}+\mathrm{BC})$
$=2 \times(C D+A D)=2 \times(a+b)$
Rhombus
Perimeter of rhombus ABCD = AB +BC +CD +AD
As lengths of all sides are equal i.e. AB = BC = CD = AD = a
Perimeter $=4 \times A B=4 \times \mathrm { Length~of~any~side. } = 4 \times a$
Kite
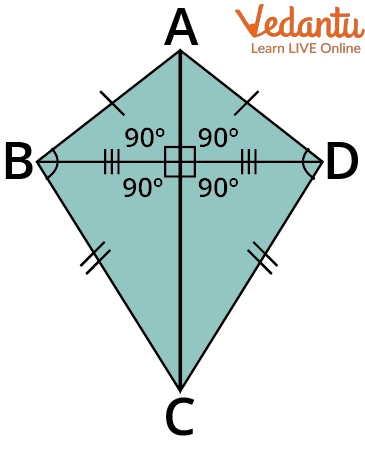
A Kite
Here AB = AD=a, BC =CD=b
Perimeter of kite ABCD = AB +BC +CD +AD
$=2 \times(A B+B C)=2 \times(a+b)$
Trapezium
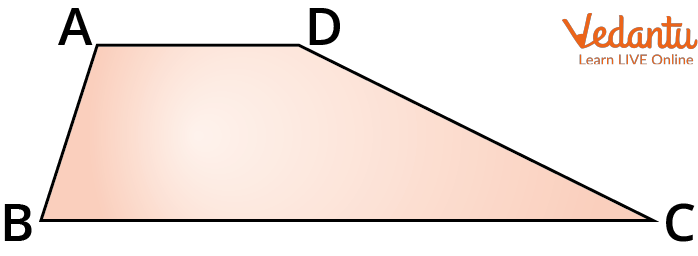

A Trapezium
All sides are unequal
Perimeter of Trapezium ABCD = AB + BC + CD + AD
Perimeter of Cyclic Quadrilateral
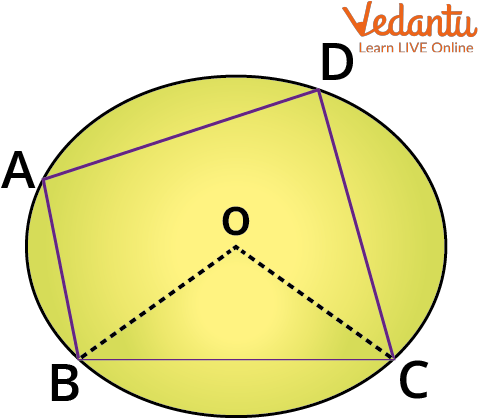
Cyclic Quadrilateral
A quadrilateral circumscribed in a circle is called a cyclic quadrilateral. It means that all four vertices of a quadrilateral lie in the circumference of the circle.
The perimeter of a cyclic quadrilateral is = AB +BC+CD+DA
Semi perimeter $=\mathrm{s}=\dfrac{AB+BC+CD+AD}{2}$
Solved Example
Q1. What will be the perimeter of a trapezoid with sides of 2 cm, 5 cm, 8 cm, and 12 cm?
Ans: Given the sides of a are Trapezoid 2 cm, 5 cm, 8 cm, and 12 cm.
Therefore, perimeter of Trapezoid is:
P = (2 cm + 5 cm +8 cm + 12 cm) = 27 cm
Practice Questions
Q1. Find the perimeter of the ceiling shaped like a rectangle of width 80m and length 30m.
Ans: 220m
Q2. Find the perimeter of the kite shaped like a rhombus of side length 8 m.
Ans: 32m
Summary
Perimeter of a quadrilateral is given by the sum of lengths of all sides. The perimeter of quadrilateral formula are-
FAQs on Perimeter of a Quadrilateral
1. What is the basic formula to find the perimeter of any quadrilateral?
The perimeter of any quadrilateral is the total length of its boundary. The basic formula is to simply add the lengths of its four sides. If the side lengths are a, b, c, and d, the perimeter (P) is calculated as: P = a + b + c + d. This formula applies to all types of quadrilaterals, including squares, rectangles, rhombuses, and irregular quadrilaterals.
2. How is the perimeter of a quadrilateral different from its area?
The perimeter and area of a quadrilateral measure two completely different properties.
- The perimeter is the total distance around the outside of the quadrilateral. It is a one-dimensional measure, expressed in units like centimetres (cm) or metres (m). Think of it as the length of a fence needed to enclose a plot of land.
- The area is the total space enclosed within the boundaries of the quadrilateral. It is a two-dimensional measure, expressed in square units like square centimetres (cm²) or square metres (m²). This would be the amount of grass inside the fenced plot of land.
3. How can you find the perimeter of a quadrilateral if the lengths of all four sides are not given?
If not all side lengths are provided, you must use the specific properties of the quadrilateral in question. For example:
- For a parallelogram or rectangle: Opposite sides are equal in length. If you know the length and width, you know all four sides.
- For a rhombus or a square: All four sides are equal. Knowing the length of just one side is enough to find the perimeter (P = 4 × side).
- For a kite: Pairs of adjacent sides are equal. If you know the lengths of two unequal adjacent sides, you can determine the lengths of all four sides.
4. How do you calculate the perimeter of a quadrilateral using its coordinates on a plane?
To find the perimeter of a quadrilateral when you only have the coordinates of its four vertices (A, B, C, D), you must calculate the length of each side using the distance formula: d = √[(x₂-x₁)² + (y₂-y₁)²]. You need to apply this formula four times to find the lengths of sides AB, BC, CD, and DA. Finally, add these four lengths together to get the total perimeter.
5. Are there simplified formulas for the perimeters of special quadrilaterals?
Yes, while the general formula (sum of all sides) always works, special quadrilaterals have simpler formulas based on their properties:
- Square: P = 4 × s (where 's' is the side length)
- Rectangle: P = 2 × (l + w) (where 'l' is length and 'w' is width)
- Rhombus: P = 4 × s (where 's' is the side length)
- Parallelogram: P = 2 × (a + b) (where 'a' and 'b' are the lengths of adjacent sides)
6. Can two different quadrilaterals have the same perimeter but a different area?
Absolutely. The shape of a quadrilateral significantly impacts its area, even if the perimeter remains constant. For example, a rectangle with sides 9 cm and 1 cm has a perimeter of 20 cm and an area of 9 cm². However, a square with sides of 5 cm also has a perimeter of 20 cm, but its area is much larger at 25 cm². This shows that perimeter does not determine area.
7. What are some real-world examples where calculating the perimeter of a quadrilateral is important?
Calculating the perimeter of a quadrilateral is a practical skill used in many real-life situations. Some common examples include:
- Fencing and Boundaries: Determining the amount of fencing needed for a four-sided garden, park, or plot of land.
- Construction and Decor: Measuring the length of skirting board or decorative trim required for a room.
- Crafts and Design: Calculating the length of ribbon or fabric needed to create a border on a quilt or a picture frame.









