




Simple Methods to Solve Percentage Questions for Students
The topic ‘Percentage’ is a very important concept because students use it regularly in various mathematical activities and day-to-day activities. So, it is essential to build the concept of percentage as future Maths concepts build upon prior knowledge. Learning the concept of percentage starts in third grade. It plays a crucial role throughout your life while solving mathematical problems.
So, in this article, we will discuss the definition of percentage, examples of percentage, and how to calculate it.
Let’s start with the definition of percentage.
What is Percentage?
A percentage in Mathematics is a number or ratio that is represented as a fraction of 100. The word ‘percent’ is derived from the Latin word ‘per centum’ which means “by a hundred”. Percentage is denoted by the symbol ‘%’. It is a dimensionless number and has no units.
Examples of Percentages
Percentage basically means a part per hundred. It can be expressed in fraction form as well as decimal form.
For example, if we say 25%, it means 25 out of 100. So, 25% is equivalent to the fraction 25/100 or 0.4 in decimal form.
Here are some examples of percentages.
10% is equivalent to 10/100 or 0.1
20% is equivalent to 20/100 or 0.2
25% is equivalent to 25/100 or 0.25
50% is equivalent to 50/100 or 0.5
75% is equivalent to 75/100 or 0.75
90% is equivalent to 90/100 or 0.9
100% is equivalent to 100/100 or 1
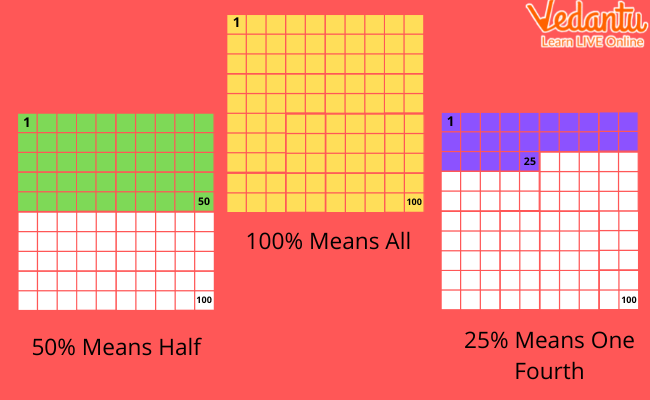
Examples of Percentage
Percentage Formula
To find out the share of a whole in terms of 100, we use the percentage formula. You can express a number as a fraction of 100 by using the percentage formula.
First, divide the value by the total value and then multiply it by 100 to get the percentage.
Percentage formula = (Value/Total value) × 100
For example, 4/5 × 100 = 0.8 × 100 = 80%
How to Calculate Percentage?
Follow the below steps to calculate the percentage of a number.
To find out the percentage of a number if the given number is in the decimal form, you have to multiply the decimal number by 100.
For example, to convert 0.6 to a percentage, you need to multiply 0.6 by 100. So, we will get 0.6 × 100 = 60%.
To find out the percentage of a number if the given number is in fractional form, first, you have to convert it to a decimal form and then multiply it by 100.
For example, to convert 1/4 to percentage, first you need to convert 1/4 to the decimal form that is 0.25 and then multiply 0.25 by 100. So, we get 0.25 × 100 = 25%.
Solved Examples
1. Convert 0.32 to percentage.
Solution: Multiplying 0.32 by 100, we get 0.32 × 100 = 32% as the answer.
2. Convert the fraction 23/25 to percentage.
Solution: Converting 23/25 to a decimal value, we get 0.92.
So, 0.92 × 100 = 92% is the answer.
3. Convert 75% to a decimal value.
Solution: 75% means 75 out of 100. So, we can write it as 75/100.
By simplifying this fraction, we get 3/4.
Then, converting 3/4 to a decimal value, we get 0.75.
4. Convert 2.5% to fractional form.
Solution: 2.5% means 2.5 out of 100. So, we can write it in the fraction form as
2.5/100.
By simplifying the fraction, we get 1/40.
5. Find the value: 7.5% of 500.
Solution:
=(7.5/100) × 500
= (3750)/100
= 37.5
6. The number 450 is what percentage of 1200?
Solution:
=(450/1200) × 100
By simplifying the fraction, we get
= (3/8) × 100
= 0.375 × 100
= 37.5%
So, the number 450 is 37.5% of 1200.
Conclusion
Possessing knowledge of how to calculate percentages is not only helpful for you to excel in Mathematics but also to apply outside the class and solve practical problems involving percentages. This article provides a step-by-step guide on how to calculate percentages with examples.
FAQs on How to Calculate the Percentage of a Number
1. What does it fundamentally mean to find the percentage of a number?
Finding the percentage of a number means calculating a specific part of that number, where the percentage itself represents a fraction out of 100. For instance, finding 50% of 20 is the same as calculating half (or 50/100) of 20, which is 10. It is a way to express a proportional part of a whole.
2. What is the standard formula to calculate the percentage of a number with an example?
The standard formula is: Value = (Percentage/100) × Total Number. For example, to calculate 25% of 80, you would set it up as:
- Value = (25 / 100) × 80
- Value = 0.25 × 80
- Value = 20
So, 25% of 80 is 20.
3. How is the concept of finding a percentage of a number applied when calculating exam marks?
This concept is crucial for understanding academic performance. If a student scores 80% in a test that has a total of 50 marks, you can find the actual marks obtained by calculating (80/100) × 50 = 40 marks. It helps translate a percentage score into a tangible value.
4. How do we use the percentage of a number in real-world financial situations like discounts?
In finance, this calculation is used constantly. For example, if an item costing ₹1,500 has a 20% discount, you find the discount amount by calculating (20/100) × 1,500 = ₹300. The final price would be ₹1,500 - ₹300 = ₹1,200. It is also used for calculating tax, interest, and tips.
5. Why is it essential to convert a percentage into a decimal or fraction before calculating?
A percentage is a form of representation, not a number for direct arithmetic. The '%' symbol is a shorthand for 'per hundred' (or /100). To perform a mathematical operation like multiplication, you must first convert the percentage into its true numerical value, which is either a fraction (e.g., 40% = 40/100) or a decimal (e.g., 40% = 0.40). Multiplying by just '40' would yield an incorrect, much larger result.
6. What is a common mistake students make when finding the percentage of a number?
A frequent error is forgetting to divide the percentage value by 100. For instance, when asked for 15% of 60, a student might incorrectly multiply 15 × 60. The correct procedure is to first convert the percentage to a decimal or fraction (15/100 = 0.15) and then multiply that by the number: 0.15 × 60 = 9.
7. Is finding 'x percent of y' the same as finding 'y percent of x'? Why?
Yes, they are always the same, which can be a useful mental math shortcut. This is because multiplication is commutative (the order of numbers doesn't change the result).
- x% of y is (x/100) × y
- y% of x is (y/100) × x
Since (x/100) × y = x × y / 100, and (y/100) × x = y × x / 100, the results are identical. For example, 20% of 50 (which is 10) is the same as 50% of 20 (which is also 10).
8. Can you calculate a percentage greater than 100% of a number, and what would it signify?
Yes, you can. A percentage greater than 100% signifies a value that is more than the original whole number. For example, finding 150% of 40 means you are looking for a value that is one and a half times 40. The calculation is (150/100) × 40 = 1.5 × 40 = 60. This is commonly seen in contexts of growth, profit, or population increase.









