




How to Solve Matchstick Pattern Problems Step by Step
The linear relationships form the basis of each matchstick pattern. This indicates that a constant number is added to the previous term to represent the rise in matches required for the 'following' term. Even the most basic items we use on a daily basis can be used to create patterns. We will take a deep insight into the matchstick patterns in this article.
Patterns in Algebra
Mathematics covers the study of numbers and the various ways that they are listed. Mathematical patterns can take many different forms, including numerical patterns, visual patterns, logic patterns, word patterns and more. Since kids are familiar with even numbers, odd numbers, skip counting, etc., which helps in learning these patterns quickly, the number pattern is the most frequently used one.
Sequence or Series in Algebra
A series or sequence that frequently repeats itself is referred to as a pattern. In our daily lives, we notice patterns in things like colours, behaviours, shapes, numbers, etc. They can be finite or infinite and related to any phenomenon or thing. A group of integers that are arranged in a pattern according to a specific rule is called a pattern in Mathematics. These guidelines specify how to compute or resolve issues. For instance, every number in the series 3, 7, 11, 15,? increases by 4. The pattern predicts that the unknown value will be 15 + 4 = 19.
Matchsticks Shapes
We may better understand the fundamental idea of variables by using matchstick patterns. Here are some matchstick shapes created by students. The objective is to determine the number of matchsticks required to create L-shaped patterns.
L-shape Pattern
The objective is to determine the number of matchsticks required to create L-shaped patterns. A student picks up two matchsticks and shapes them into the letter L. Another student picks up four matchsticks and shapes them into a pattern of two Ls. We'll add up the total number of Ls made and matchsticks required to make the pattern.
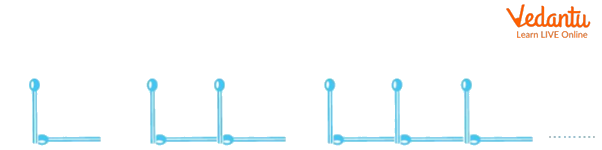
Matchsticks Pattern of L’s
The required number of matchsticks is twice the number of Ls created. So, we can write for the number of matchsticks in this pattern in algebra,
Required number of matchsticks = 2 \[ \times \]number of Ls formed
For the sake of simplicity, let's represent the number of Ls with the letter\[n\]. Thus, \[n\] can be any natural number, such as 1, 2, 3, 4, or 5, depending on how many Ls are created. \[n\] for one L, \[n\] for two Ls, and so on. Then, we can also write,
Required number of matchsticks = \[n\].
For\[n\] to be equal to 1, the required number of matchsticks is 2.
For\[n\] to be equal to 2, the required number of matchsticks is 4, etc.
Triangles Pattern
In a similar way, look at the following pattern of triangles.

Matchstick Pattern of Triangles
The number of matchsticks in this pattern is 3, 5, 7, and 9, which is more than twice the number of triangles in the pattern. Let \[x\] represent the number of triangles, and then the number of matchsticks in this pattern is \[2x + 1\].
Square Pattern
Now Look at the square matchstick pattern in the figure below. The squares are joined together. A matchstick is shared by two adjacent squares. Discovering the rule that specifies the number of matchsticks will need careful observation of the patterns.
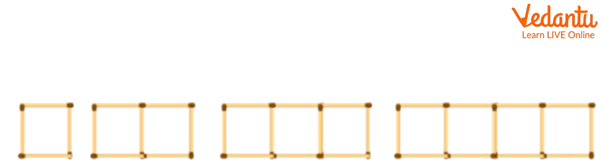
Matchsticks Pattern of Squares
The number of matchsticks in the above matchstick patterns is 4, 7, 10 and 13, which is more than thrice the number of squares in the pattern. So, the algebraic statement \[3x + 1\], where \[x\] is the number of squares, can be used to define this pattern.
Matchsticks Patterns Examples
Find the rule that specifies how many matchsticks are needed to create each of the following matchstick shapes. When writing the rule, use a variable.
A pattern of the letter E
A pattern of the letter U
A pattern of the letter V
Explanation: To determine the number of matchsticks needed to create the specified matchstick patterns, we use the algebraic idea. We can create a matchstick pattern by increasing the number of sticks needed to create the given patterns.
The letter E is formed by five matchsticks. So, the rule is to form a pattern of the letter E is \[n\], where n is the number of E.
The letter U is formed by three matchsticks. So, the rule is to form a pattern of the letter U is \[n\], where n is the number of U.
The letter V is formed by two matchsticks. So, the rule is to form a pattern of the letter V is \[n\], where n is the number of V.
Interesting Facts
In order to discover a general rule that can be represented in various ways, the relationship between the number of matches for a term and the number of terms in a pattern are investigated.
There are different types of patterns in algebra:
Arithmetic Sequence
Cube Numbers
Geometric Sequence
Triangular Numbers
Solved Questions
1. How many matchsticks are required to make 8 squares?
Ans: We know the rule to make a matchstick pattern of squares which is \[3x + 1\], where \[x\] is the number of squares.
So here \[x\], then \[3x + 1 = 3 \times 8 + 1 = 25\]
The number of matchsticks required to make 8 squares is 25.
2. With 17 matchsticks, how many triangles are possible?
Ans: We know the rule to make a matchstick pattern of triangles which is \[2x + 1\], where \[x\] is the number of triangles.
So given that \[2x + 1\]
\[2x = 16\] then \[x = 8\]
8 triangles are possible with 17 matchsticks.
Key Features
We learned that a variable can be used to represent an unknown quantity.
We learned the general formula for the number of matchsticks needed to form a particular shape.
We studied the methods for utilising matchsticks to form letters and other forms.
The repetition rate of a given shape varies; it can be 1, 2, 3, ..., etc. It is a variable that is identified by a letter, such as n.
Practice Questions
1. How many matchsticks are required to make three F's patterns?
Answer: 4
2. Find the rule that specifies how many matchsticks are needed to create the following patterns. To write the rule, use a variable.
a pattern of letter-A
Answer: 6n where n is the number of A.
FAQs on Matchstick Patterns: Concepts, Tricks & Practice
1. What are matchstick patterns in mathematics?
Matchstick patterns are sequences formed by arranging matchsticks to create repeated geometric shapes. Each step or term in the pattern adds a fixed number of matchsticks following a rule. These patterns help introduce students to ideas like sequences and algebra.
2. How can matchstick patterns help in understanding algebraic expressions?
When creating matchstick patterns, students notice that each stage increases by a set amount. This regular growth helps students write algebraic expressions, such as $3n + 2$, to describe how the pattern builds as the position number $n$ changes.
3. What is the general formula for finding the number of matchsticks in a pattern?
The general formula for matchstick patterns is usually $an + b$, where $n$ is the term number, $a$ is the increase per stage, and $b$ is the starting number. This formula predicts the number of matchsticks needed for any term in the sequence.
4. Can you give an example of a simple matchstick pattern?
A simple matchstick pattern is forming squares in a row, where each new square shares one side with the previous. For $n$ squares, the number of matchsticks is $3n + 1$. This example introduces counting and pattern recognition.
5. Why do matchstick patterns often have a linear relationship?
Most matchstick patterns show a linear relationship because each new shape in the sequence adds the same number of matchsticks. This constant difference creates a line when the number of matchsticks is plotted against the term number $n$.
6. What skills do students develop by working with matchstick patterns?
By exploring matchstick patterns, students develop skills such as:
- Recognizing patterns
- Writing algebraic expressions
- Using sequences
- Visualizing problem-solving strategies
7. How do you find the rule for a given matchstick pattern?
To find a rule for a matchstick pattern, observe how many matchsticks increase from one term to the next, then write an expression using this growth. For example, if each figure adds $2$ sticks, the rule may look like $2n + b$.
8. What are some common shapes used in matchstick patterns?
Common shapes used in matchstick patterns include:
- Squares
- Triangles
- Rectangles
- Stairs
9. How can matchstick patterns introduce the concept of sequences?
Using matchstick patterns helps students see that sequences are sets of numbers that follow a rule. By counting matchsticks in each shape, learners see how each term connects to the next, building a clear understanding of sequences in math.
10. How are matchstick patterns used in classroom activities?
Teachers use matchstick patterns during classroom activities to encourage hands-on learning. Students physically build the patterns, record data, find growth rules, and write formulas, making abstract math concepts like patterns and algebra more concrete and engaging.
11. How can students write equations for matchstick patterns?
Students can write an equation for matchstick patterns by determining the number added at each step and the initial value. The formula typically takes the form $y = an + b$, where $a$ and $b$ are found by analyzing pattern growth.





















