




Stepwise Guide: Applying the Sandwich Theorem to Trigonometric Limits
We will discuss a crucial idea utilised in calculus and its limits in this topic. We'll talk about the Sandwich theorem notion. This theorem is very easy to comprehend and has numerous calculus applications. It is particularly useful for applying trigonometric functions. A thorough comprehension of the sandwich theorem will be useful not only for calculus but also for other ideas like the binomial theorem.
History of Carl Friedrich Gauss
In an effort to compute π, the mathematicians Archimedes and Eudoxus utilised the Sandwich theorem for the first time geometrically. Carl Friedrich Gauss then expressed it in more contemporary terms. Johann Carl Friedrich Gauss was a German mathematician and physicist who made a significant impact on a variety of scientific and mathematical subjects.

Carl Friedrich Gauss (30 April 1777 – 23 February 1855)
What is the Sandwich Theorem in Limits?
Let f, g, and h be real functions such that for any x in the shared definition domain, f(x) g(x) h(x) occurs. When \[a\] is a real number, then
\[\begin{array}{l}\mathop {{\rm{\;}}\lim }\limits_{x \to a} f\left( x \right)\;\; = \;\mathop {lim}\limits_{x \to a} h\left( x \right)\; = \;t\\{\rm{then}}\;\mathop {\lim }\limits_{x \to a} g\left( x \right)\; = \;t\end{array}\]
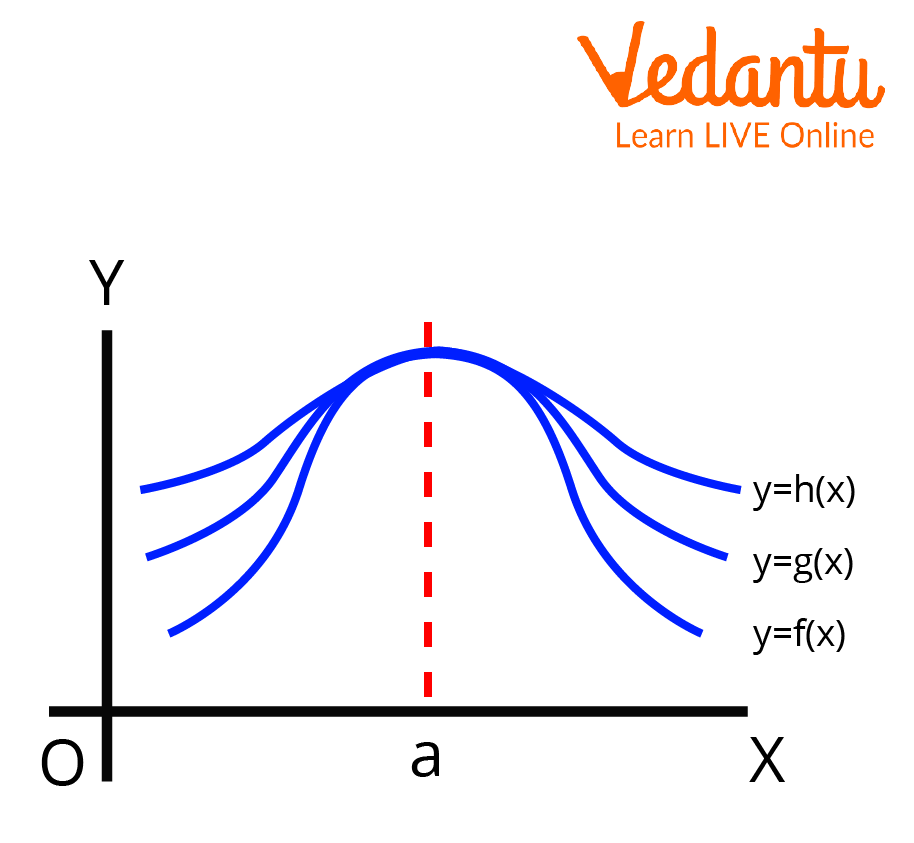
Sandwich Theorem in Limits
Sandwich Theorem Proof
Let's examine the geometric proof for the aforementioned claim using a trigonometric inequality.
Think of the disparity as
\[\cos x\; < \;\sin x\;/\;x\; < 1\]

Sandwich Theorem Proof
We can see the triangles ΔABE, ΔADF, ΔADB, and sector ADB in the above diagram.
\[\begin{array}{l}Area\;\left( {\Delta ABD} \right)\; < \;Area\;\left( {sector\;ADB} \right)\; < \;Area\;\left( {\Delta ADF} \right)\\\; \Rightarrow 1/2.AD.EB\; < \;x/2\pi .\pi .A{D^2}\; < \;1/2.AD.DF\end{array}\]
By eliminating the common terms from all sides,
\[{\rm{EB}} < x.AD < {\rm{ DF}}\]
Since angle A = angle X,
\[EB\; = \;AB\; \sin x\] (from Δ ABE),
and \[\sin A\; = \;EB/AB\].
\[DF\; = \;AD \tan X\] because \[\tan A\; = \;DF/AD\].
However, \[\tan A\; = \;\sin X/\cos x\;\] and \[AB\; = \;AD\].
Consequently,
\[\begin{array}{l}AD.\sin A\; < x.AD < \;AD.\sin A\;/\;\cos A\\ \Rightarrow \; = \;1\; < x\;/\;\sin X < \;1\;/\;\cos X\end{array}\]
By taking reciprocals,
\[\cos x\; < \;\sin x\;/\;x\; < 1\]
Hence proved.
We can simply demonstrate some other trigonometric identities using the above theory, including
\[\begin{array}{l}li{m_{x - > 0}}\sin x/x\; = 1\;\\li{m_{x - > 0}}\;\left( {1\;--\;\cos x} \right)/x\; = 0\end{array}\]
Limitations of Sandwich Theorem
The Sandwich theorem is not applicable if left and right function limits are not equal.
The Sandwich Theorem does not apply if we know the limits of any of two functions other than both extreme functions.
Applications of Sandwich Theorem
To determine the limits of specific trigonometric functions, we can utilise the Sandwich rule.
It can be applied to link certain sequences between other known sequences that also converge to the same place in order to demonstrate the convergence of those sequences.
Interesting Fact
If \[f\left( x \right) \le g\left( x \right)\] when x is close to \[\alpha \] (unless perhaps at an \[\alpha \]), then $\underset{x\to \alpha }{\mathop{\lim }}\,f\left( x \right)~\underset{x\to \alpha }{\mathop{\lim }}\,g\left( x \right)$.
Solved Examples of Limits of Trigonometric Functions Using Sandwich Theorem
1. Evaluate the limit for the following tangent function \[lim{_{\;x - > 0}}\;\tan x\;/\;x\].
Ans: Using the trigonometric identity,
\[\begin{array}{l}\tan x\; = \dfrac{{\;\sin x}}{{\cos x}}\\\therefore \mathop {\lim }\limits_{x \to 0} \;\dfrac{{\sin x}}{{x\cos x}}\; = \;\mathop {\lim }\limits_{x \to 0} \;\dfrac{{\sin x}}{x}\cdot\mathop {\lim }\limits_{x \to 0} \;\dfrac{1}{{\cos x}}\end{array}\]
And from the Sandwich theorem, we know,
\[\begin{array}{l}li{m_{x - > 0}}\sin x/x\; = 1\\\;li{m_{x - > 0}}\;1/\cos x\; =1\end{array}\]
Therefore,
\[1\cdot\,1\; = \;1\]
2. Prove \[\mathop {\lim }\limits_{x \to 0} \sin x\; = \;0\].
Ans. As known,
$-x\leqslant\sin x\leqslant x\, for \, all\,x \geqslant 0$
\[\begin{array}{l} \Rightarrow \mathop {\lim }\limits_{x \to 0} \left( { - x} \right)\; = \;0\;\;{\rm{and}}\\\mathop {\lim }\limits_{x \to 0} \left( x \right)\; = \;0\end{array}\]
By Sandwich Theorem,
\[\mathop {\lim }\limits_{x \to 0} \left( {Sinx} \right)\; = \;0\]
3. Evaluate \[\mathop {\lim }\limits_{x \to 0} x\dfrac{{secx - 1}}{x}\]
Ans. As we know,
\[\sec x\; = \dfrac{{\;1}}{x}\]
So,
\[\begin{array}{l}\mathop {\lim }\limits_{x \to 0} x\dfrac{{secx - 1}}{x} = \mathop {\lim }\limits_{x \to 0} x\dfrac{{\dfrac{1}{{\cos x}} - 1}}{x}\\\mathop {\lim }\limits_{x \to 0} x\dfrac{{1\; - \cos x}}{{x\cos x}}\\\mathop { \Rightarrow \lim }\limits_{\;\;\;\;\;\;x \to 0} x\left( {\dfrac{1}{{\cos x}}} \right)\left( {\dfrac{{1\; - \cos x}}{x}} \right)\\ \Rightarrow \mathop {\lim }\limits_{x \to 0} x\left( {\dfrac{1}{{\cos x}}} \right)\mathop {\lim }\limits_{x \to 0} x\left( {\dfrac{{1\; - \cos x}}{x}} \right)\\ \Rightarrow 1 \times 0\\ \Rightarrow 0\end{array}\]
Conclusion
In this article, we have thoroughly discussed the Sandwich theorem and its proof. From the discussion above, about the Sandwich theorem we can conclude that the sandwich theorem allows us to determine the limit of a single function by using the limits of the two other functions that it is "sandwiched" between as a starting point. When a function gets complex or intricate, or perhaps when we are unable to identify the limit using other techniques, we apply the Sandwich theorem to determine its limit. The limits of trigonometric functions are most frequently found using this method.
Important Points
This theorem is probably utilised to establish the limit of the function in question.
All the functions considered must be real.
Important Formula From the Theorem
According to the Sandwich theorem,
If \[\begin{array}{l}\mathop {{\rm{\;}}\lim }\limits_{x \to a} f\left( x \right)\;\; = \;\mathop {lim}\limits_{x \to a} h\left( x \right)\; = \;t\\{\rm{then}}\;\mathop {\lim }\limits_{x \to a} g\left( x \right)\; = \;t\end{array}\]
FAQs on Limits of Trigonometric Functions Using the Sandwich Theorem
1. What is the Sandwich Theorem for limits?
The Sandwich Theorem, also known as the Squeeze Theorem, is a fundamental concept in calculus used to find the limit of a function. It states that if a function f(x) is 'sandwiched' or 'squeezed' between two other functions, g(x) and h(x), near a certain point 'c', and if both g(x) and h(x) approach the same limit L at that point, then f(x) must also approach the same limit L.
2. Why is the Sandwich Theorem needed to find the limit of certain trigonometric functions like sin(x)/x?
Directly substituting x = 0 into the expression sin(x)/x results in the indeterminate form 0/0. We cannot determine the limit through simple algebraic manipulation or substitution. The Sandwich Theorem provides a rigorous method to evaluate this limit by trapping the function sin(x)/x between two simpler functions whose limits are known and equal as x approaches 0. This allows us to find the precise value of the limit without encountering the 0/0 issue.
3. How is the proof for the limit of (sin x)/x as x approaches 0 derived using the Sandwich Theorem?
The proof relies on a geometric construction using a unit circle. For an angle x (in radians, close to 0), we can establish an inequality by comparing the areas of three shapes: a small triangle, a circular sector, and a large triangle. This comparison leads to the inequality cos(x) < (sin x)/x < 1. As we take the limit as x approaches 0 for all parts of the inequality:
- The limit of cos(x) as x approaches 0 is 1.
- The limit of 1 as x approaches 0 is 1.
Since (sin x)/x is squeezed between two functions that both approach 1, the Sandwich Theorem guarantees that the limit of (sin x)/x as x approaches 0 is also 1.
4. What are the key conditions for applying the Sandwich Theorem?
To successfully apply the Sandwich Theorem to find the limit of a function f(x) as x approaches 'c', three conditions must be met:
- The Inequality: The function f(x) must be bounded between two other functions, g(x) and h(x). This means g(x) ≤ f(x) ≤ h(x) must hold true for all x in an open interval around 'c' (though not necessarily at 'c' itself).
- Existence of Limits: The limits of the two outer functions, g(x) and h(x), must exist as x approaches 'c'.
- Equal Limits: The limits of the two outer functions must be equal. That is, lim g(x) = lim h(x) = L as x approaches 'c'.
5. Can you provide a simple example of using the Sandwich Theorem for a trigonometric limit?
A classic example is finding the limit of x² sin(1/x) as x approaches 0. We know that the sine function is always bounded between -1 and 1. So, for any x ≠ 0, we have:
-1 ≤ sin(1/x) ≤ 1
Multiplying the entire inequality by x² (which is always non-negative), we get:
-x² ≤ x² sin(1/x) ≤ x²
Now, we find the limits of the outer functions as x approaches 0:
lim(-x²) = 0 and lim(x²) = 0.
Since our function is squeezed between two functions that both approach 0, by the Sandwich Theorem, the limit of x² sin(1/x) as x approaches 0 must also be 0.
6. What is the geometric interpretation behind the Sandwich Theorem proof for lim (sin x)/x?
The geometric interpretation provides a visual understanding of the proof. Imagine a sector of a unit circle with a small angle x. We can draw and compare the areas of three specific shapes:
1. The area of a small inner triangle (Area = ½ sin x).
2. The area of the circular sector itself (Area = ½ x).
3. The area of a large outer triangle (Area = ½ tan x).
Visually, it's clear that Area(small triangle) ≤ Area(sector) ≤ Area(large triangle). This translates to the inequality ½ sin x ≤ ½ x ≤ ½ tan x, which simplifies to cos x ≤ (sin x)/x ≤ 1. This geometric relationship is the foundation for 'squeezing' the function to find its limit.
7. What are the two most important trigonometric limit formulas derived from the Sandwich Theorem for the CBSE Class 11 syllabus 2025-26?
As per the CBSE Class 11 curriculum for 2025-26, there are two standard trigonometric limits whose proofs are based on the Sandwich Theorem. These are crucial for solving problems in calculus:
- lim (sin x)/x = 1 (as x approaches 0)
- lim (1 - cos x)/x = 0 (as x approaches 0)
The first formula is proven directly using the Sandwich Theorem. The second formula is derived from the first one using trigonometric identities, making both results fundamentally linked to the theorem's application.
























