




How to Find the HCF of Two Numbers Using Prime Factorisation
H.C.F stands for Highest Common Factor. To find the H.C.F of two numbers we need to factorise the numbers and then take the common factors. After which we have to multiply the common factors and get the required H.C.F. In this article, you will get to know how to find HCF of two numbers, hcf of two numbers by division method and hcf of two numbers formula. To find the HCF by division method you will have to divide the larger number by the smaller number, until we get a remainder zero or unless further division is not possible.
H.C.F of Two Numbers
To find the HCF of any two numbers we need to follow the following steps:
Step 1: Take out the factors of the numbers. Let us suppose that the two numbers are 96 and 112.
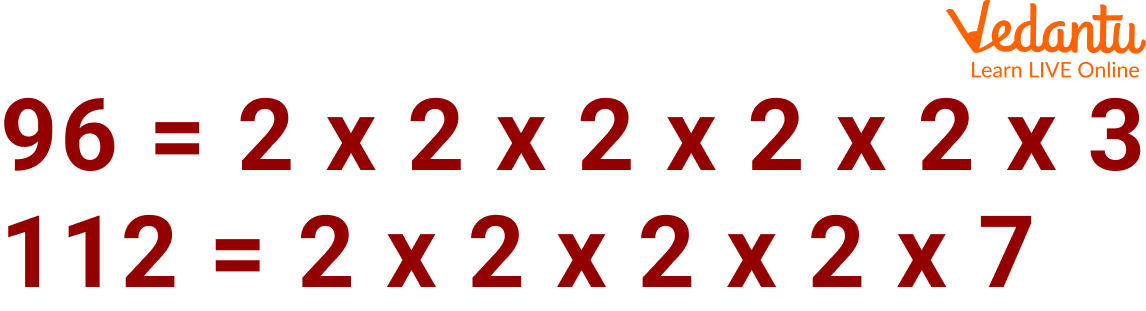
Carrying Out HCF of 96 and 112
Step 2: Now we need to look at the common factors (C.F) of the numbers as shown below.
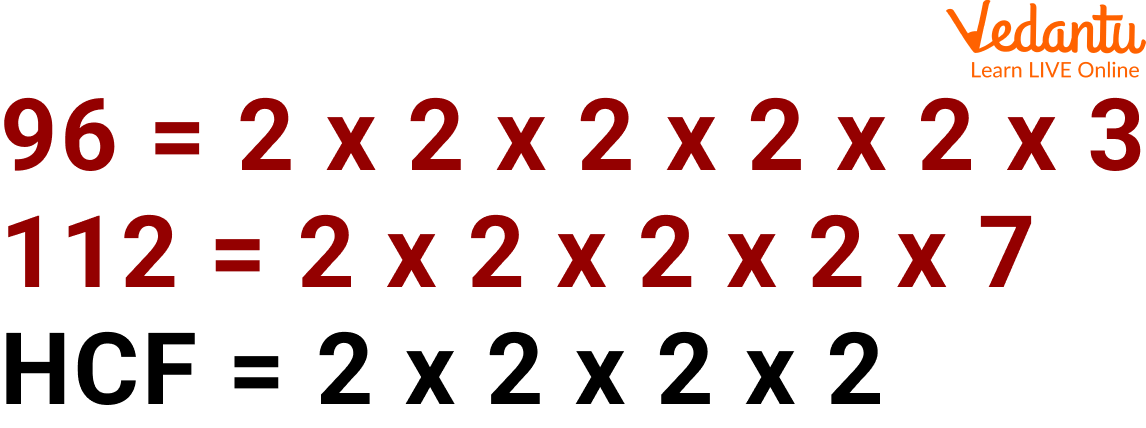
Carrying out HCF of 96 and 112
Step 3: We can see clearly the common factors highlighted in the colour blue. Now we will take the common factors from both the numbers and multiply them to get the HCF.
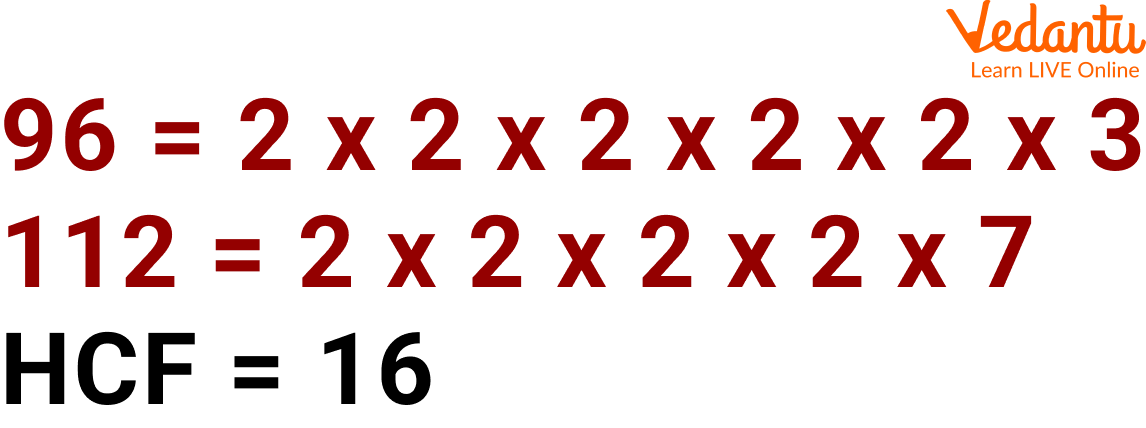
The HCF of 96 and 112 is 16
HCF of Two Numbers by Division Method
To find the HCF by division method you will have to divide the larger number by the smaller number and then again the remainder will become the divisor and divide the smaller number until we get a remainder zero or such that further division is not possible. Let’s practically understand this with the help of some examples.
Let us take two numbers, 46 and 242.
To find the HCF by division method we will divide the larger number by the smaller number.

HCF of 46 and 242
Hence, the required HCF of the numbers 46 and 242 is 2.
This method is also known as Euclid’s Division method named after the mathematician Euclid.
Let us consider a few more examples to understand the division method more clearly.
Solved Examples
Example 1: Find the H.C.F of 50 and 75.
Ans: First, you need to find the factors of the given numbers.

Step 1 of carrying out HCF of 50 and 75
After writing the factors then we will find the common factors. Here in this case the common factors are 5 and 5.

Step 2 of carrying out HCF of 50 and 75
After getting the common factors we will multiply the common factors to get the required H.C.F

HCF of 50 and 75 is 25
We can see clearly that the H.C.F of 50 and 75 is 25.
Example 2: Find the H.C.F of 432 and 876.
Ans: First, we need to find the factors of the given numbers.
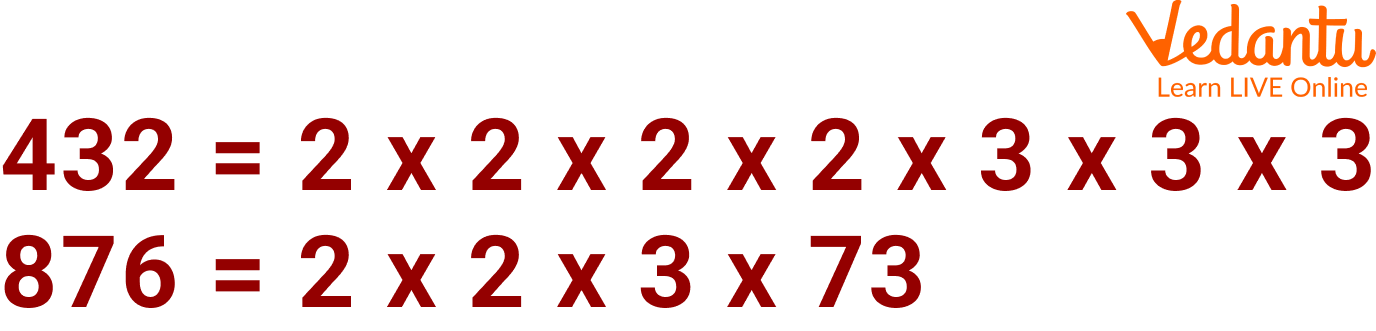
Step 1 of carrying out HCF of 432 and 876
Now taking out the common factors from the factors above. We can see that the common factors are 2, 2 and 3.
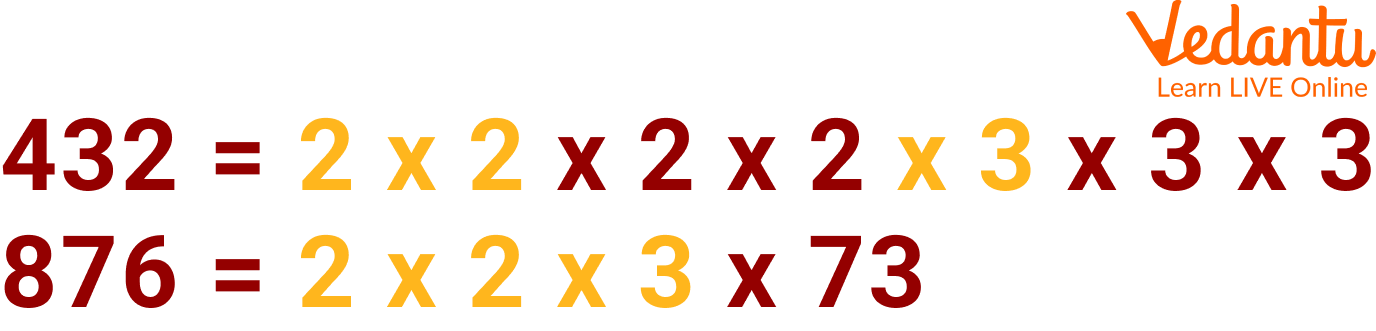
Step 2 of carrying out HCF of 432 and 876
Now after multiplying the common factors we will get the required H.C.F of the given numbers.
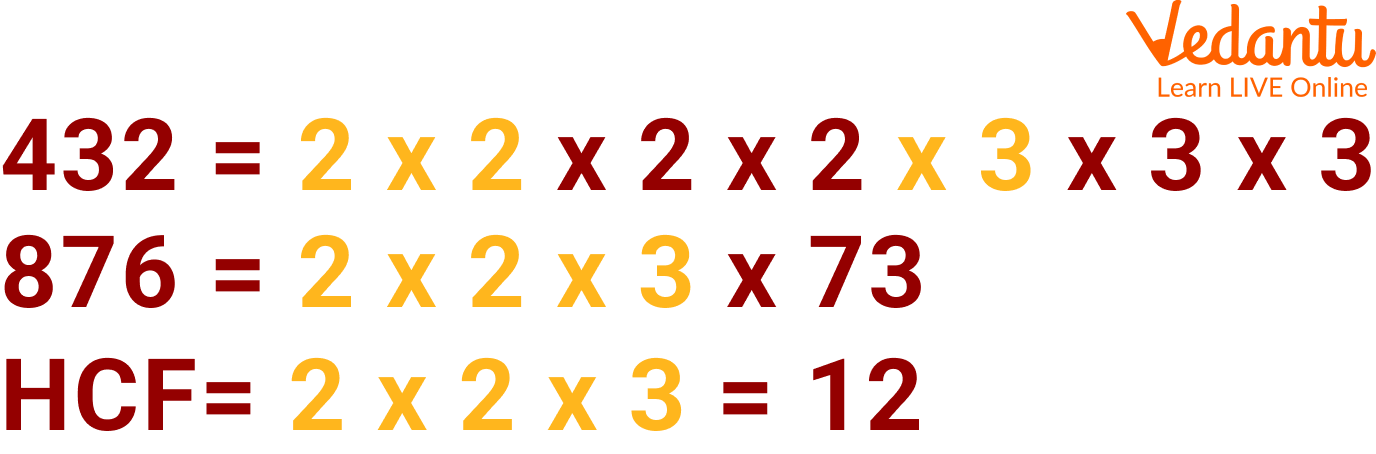
The HCF of 432 and 876 is 12
Hence, the required H.C.F of the given numbers is 12.
Example 3: Find the HCF of 1334 and 8948.
Ans: We can see that the smaller number is 1334 and the larger number is 8948 so we will divide 8948 by 1334.
Here the smallest number which divides the dividend is 2 so we can say that the HCF of the given numbers 1334 and 8948 is 2.
Example 4: What is the highest common factor of 96 and 404?
Ans: Prime factorization of 96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3
Prime factorization of 404 = 2 × 2 × 101 = 22 × 101
HCF(96, 404) = 22 = 4
Therefore, the highest common factor of 96 and 404 is 4.
Practice Questions
Q 1 Find the H.C.F of 12, 45 and 75.
Ans: 3
Q 2 Find the H.C.F of 18,30 and 42.
Ans: 6
Q 3 Find the HCF of 867 and 255.
Ans: 51
Q 4 Find the HCF of 4052 and 12576.
Ans: 4
Summary
From HCF of two numbers examples, we have learnt to find the factors and then take the common factors. Then after that multiplication of the common factors will give us the HCF. We can use the division method to find the HCF. Hence, after going through this article we have made our concepts of HCF very clear in both methods and now we know how to find HCF of two numbers. With the examples and practice problem, we will get more clarity on the topic. So after reading the article go through the practice problem to have better understanding.
FAQs on HCF of Two Numbers: Step-by-Step Guide
1. What is the Highest Common Factor (HCF) of two numbers?
The HCF of two or more numbers is the greatest positive integer that divides each of the numbers without leaving a remainder. It is also known by other names like the Greatest Common Divisor (GCD) or the Greatest Common Measure (GCM). For example, the HCF of 12 and 18 is 6, because 6 is the largest number that can divide both 12 and 18 exactly.
2. What are the main methods to find the HCF of two numbers?
There are two primary methods for finding the HCF of two numbers, as per the CBSE syllabus for the 2025-26 session:
Prime Factorisation Method: In this method, you express each number as a product of its prime factors. The HCF is the product of the lowest powers of all common prime factors.
Division Method (Euclidean Algorithm): In this method, you divide the larger number by the smaller number. Then, you divide the divisor by the remainder. This process is repeated until the remainder becomes zero. The last non-zero divisor is the HCF.
3. Can you show with an example how to find the HCF of 24 and 36?
Certainly. Let's find the HCF of 24 and 36 using the prime factorisation method, a key technique in the NCERT curriculum:
First, find the prime factors of 24: 24 = 2 × 2 × 2 × 3.
Next, find the prime factors of 36: 36 = 2 × 2 × 3 × 3.
Now, identify the common prime factors: Both numbers share two 2s and one 3.
Finally, multiply these common factors to get the HCF: HCF = 2 × 2 × 3 = 12.
Therefore, the HCF of 24 and 36 is 12.
4. What are some real-life examples of using HCF?
The HCF has several practical applications in daily life. For instance, it is used to:
Arrange items in groups: To find the largest number of rows or groups to arrange students or objects so that each group has the same number of items.
Distribute items equally: To split different quantities of items into the largest possible identical sets. For example, if you have 80 chocolates and 60 cookies, HCF helps find the maximum number of gift bags you can make with an equal number of chocolates and cookies in each.
Tiling problems: To find the largest size of square tile that can pave a rectangular floor without any cutting or wastage.
5. What is the difference between HCF (Highest Common Factor) and LCM (Lowest Common Multiple)?
HCF and LCM are related but fundamentally different concepts that are important to distinguish:
HCF (Highest Common Factor): It is the largest number that divides two or more numbers. The HCF of two numbers will always be less than or equal to the smaller of the two numbers.
LCM (Lowest Common Multiple): It is the smallest number that is a multiple of two or more numbers. The LCM of two numbers will always be greater than or equal to the larger of the two numbers.
In essence, HCF is about finding the largest common divisor, while LCM is about finding the smallest common multiple.
6. How does finding the HCF help in simplifying fractions?
The HCF is a crucial tool for simplifying fractions to their lowest terms. To simplify a fraction, you divide both the numerator and the denominator by their HCF. Since the HCF is the largest number that divides both, this one-step division ensures the fraction is reduced completely. For example, to simplify the fraction 24/36, we find the HCF of 24 and 36, which is 12. Dividing both parts by 12 gives 2/3, the simplest form of the fraction.
7. Is it possible for the HCF of two numbers to be one of the numbers itself?
Yes, this is possible. The HCF of two numbers is one of the numbers itself if and only if the smaller number is a factor of the larger number. For instance, the HCF of 12 and 24 is 12. This is because 12 divides 24 perfectly (24 = 12 × 2). In such cases, the smaller number is the greatest common divisor for both.
8. What is the relationship between the HCF and LCM of two numbers and the numbers themselves?
There is a fundamental relationship between the HCF and LCM of any two positive integers. The product of the HCF and LCM of two numbers is always equal to the product of the two numbers themselves. This can be expressed with the formula:
HCF (a, b) × LCM (a, b) = a × b
This property is very useful for finding the LCM if you know the HCF (and vice versa), and it often forms the basis of problems in school examinations.









