




Introduction
Any integer that divides a number into another number equally is considered a factor. In the division problem, for instance, \[10 \div 5 = 2\],10 has the factors 1, 2, 5, and 10. These factors can all be divided into equal groups, such as two groups of five, two groups of two, and one group of ten, which is the same as two groups of five, two groups of two, and one group of ten, and one group of ten, respectively.
Division Factor
The numbers that can divide a number exactly are called factors. There is, therefore, no remainder after division. The numbers you multiply together to obtain another number are called factors. A factor is therefore another number's divisor.
Divisor vs. Factor
Any number that divides another number is known as the divisor. However, a factor is a divisor that completely divides the integer and leaves no remainder. Therefore, any factor of a number is also its divisor. But not all factors are divisors; a number's divisors are all of its factors. In the previous illustration, the components of 20 are 4 and 5. However, dividing 20 by 3 does not result in a perfect division of the number.
How to Divide Factors?
What are the Factors of 18 (Division Method)?
Steps to find division factors of 18:
STEP 1: Using division laws, we determine the number's smallest exact prime divisor (factor). Here, the number 18 is even. It can be divided by 2. Therefore, 2 divides 18 without leaving a remainder. So, the least prime factor of 18 is 2.
STEP 2: Is to divide the supplied number (18) by its smallest prime factor, which equals 9.
STEP 3: Next, we identify the derived quotient's prime factors. Repeat steps 1 and 2 until the quotient is a prime number. Here, the quotient is 9, therefore \[9 = 3 \times 3\].
We stop the operation here because 3 is the quotient. Consequently \[18 = 2 \times 3 \times 3\].Thus, the factors of 18 are 1,2, 3, 6, 9,18.
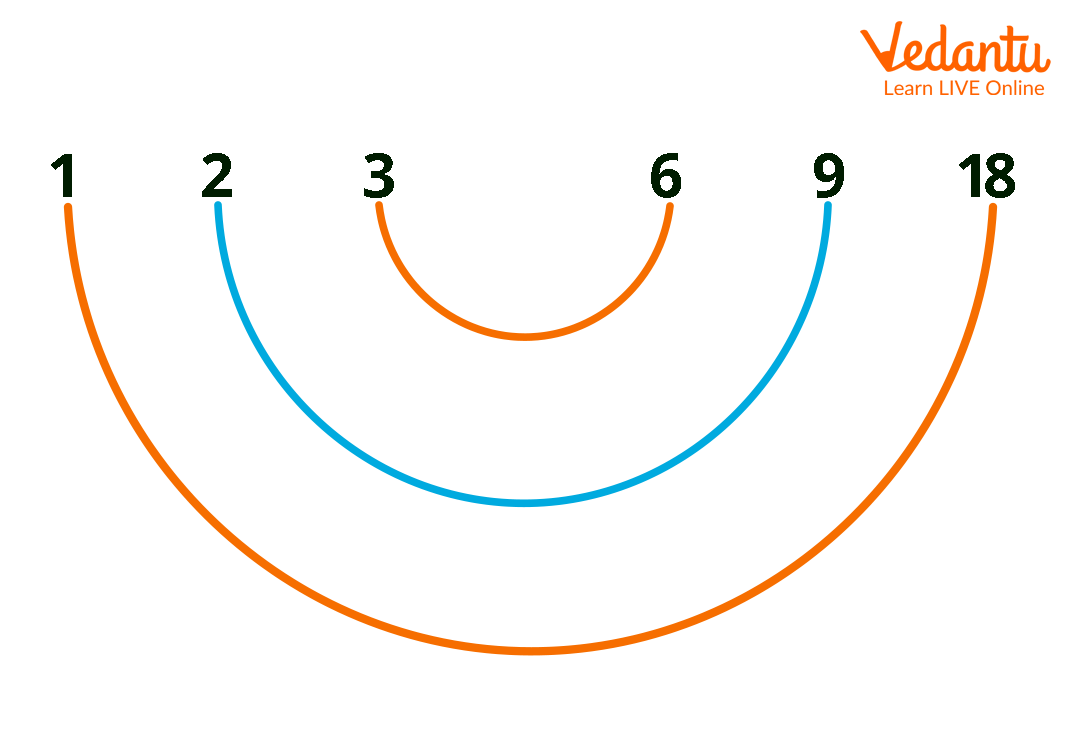
Pairs for Factors of 18
Solved Examples
Example 1: List the factors of 18 and their corresponding factor pairs in Example 1.
Ans:
\[\begin{array}{l}1 \times 18 = 18\\2 \times 9 = 18\\3 \times 6 = 18\end{array}\]
Therefore, the factors of 18 are 1, 2, 3, 6, 9, and 18.
Pairs of the factors of 18 are (1,18), (2,9), and (3,6)
Example 2: Find the common factors of 25 and 24.
Ans: The factors of 25 are as follows: 1, 5, and 25.
The factors of 24 are as follows: 1, 2, 3, 4, 6, 8, 12, and 24.
Thus, the common factor of 25 and 24 is 1.
Example 3: Find the factors of 72.
Ans: 72 is represented as the product of the following additional numbers:
\[\begin{array}{l}1 \times 72 = 72\\2 \times 36 = 72\\3 \times 24 = 72\\4 \times 18 = 72\\6 \times 12 = 72\\8 \times 9 = 72\\9 \times 8 = 72\end{array}\]
Since multiplication is currently being repeated, it must be stopped.
Conclusion
Factors and multiples by using division facts, for instance, are employed while handling money, sorting objects into boxes, looking for patterns in numbers, resolving ratios, or expanding or contracting fractions. In Mathematics, a factor is an integer that divides another number equally by itself while producing no remainder. We frequently come across factors and multiples.
FAQs on Division Factor
1. What is a factor in Maths, explained with division?
A factor is a number that divides another number completely, without leaving any remainder. For example, 4 is a factor of 20 because when you divide 20 by 4, the answer is 5 with a remainder of 0. This direct relationship with division is why factors are fundamental to understanding number properties.
2. How can you find all the factors of a number?
To find all the factors of a number, you can use the division method. Start dividing the number by 1, then 2, then 3, and so on. If a number divides the original number with no remainder, it is a factor. For example, to find the factors of 12:
- 12 ÷ 1 = 12 (so, 1 and 12 are factors)
- 12 ÷ 2 = 6 (so, 2 and 6 are factors)
- 12 ÷ 3 = 4 (so, 3 and 4 are factors)
The complete list of factors for 12 is 1, 2, 3, 4, 6, and 12.
3. What is the difference between a factor and a multiple?
The key difference lies in their relationship to the original number. A factor is a number that divides the original number, so it is always less than or equal to that number. A multiple is the result of multiplying the original number by an integer (like 1, 2, 3,...), so it is always greater than or equal to the number. For example, 3 is a factor of 12, while 24 is a multiple of 12.
4. Why is the number 1 considered a factor of every number?
The number 1 is a factor of every number because any whole number can be divided by 1 without leaving a remainder. According to the rules of division, dividing any number 'n' by 1 will always result in 'n' itself. For instance, 15 ÷ 1 = 15, and 199 ÷ 1 = 199. This makes 1 a universal factor.
5. Can a factor of a number ever be larger than the number itself?
No, a factor of a positive number cannot be larger than the number itself. A factor must divide the number evenly. If a divisor were larger, it could not divide the smaller number to produce a whole number result. The largest possible factor of any number is the number itself.
6. What are the factors of 48?
The factors of 48 are the numbers that divide 48 without leaving a remainder. By testing numbers starting from 1, we find the factors are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
7. How do you determine if 7 is a factor of 91?
To determine if 7 is a factor of 91, you perform the division: 91 ÷ 7. The result is 13 with a remainder of 0. Since the division is exact and there is no remainder, we can confirm that 7 is a factor of 91.
8. What is a real-world application of finding factors?
Finding factors is useful in real-world situations involving equal grouping or arrangement. For example, if a teacher has 30 students and wants to divide them into equal-sized groups for an activity, the factors of 30 (1, 2, 3, 5, 6, 10, 15, 30) show all the possible group sizes. The teacher could make 6 groups of 5 students or 3 groups of 10 students.









