




How to Calculate the Diameter of a Circle with Examples
We all have seen a circle and understand its shape and structure. Also, some of our daily used objects are circular in shape like plates, balls, mirrors, etc. However, did you know what is the diameter of a circle? You are aware of the term radius but have you ever heard about the diameter of a circle? Have you ever done a question associated with the diameter of a circle? The diameter of a circle is double the radius of the circle. It's the string line passing through the center of the circle connecting the two adjacent points on the circumference of the circle.
In this article, we are going to understand the concept of the diameter of a circle, what is diameter, the diameter symbol, and also the formula for the diameter of the circle.
Diameter of a Circle
A circle is defined as the collection of points at a particular distance from the center point in a plane. The distance between the center and any point on the plane is termed radius. In the same manner, the distance from one point on the surface of the circle to the other point on its surface and passing through the center of the circle is termed its diameter.
In different words, the diameter is defined as double the radius of the circle.

Diameter of a Circle
What is Diameter?
In order to understand the concept of a diameter, take any circular object like a bangle or a plate. You'll see the circumference of a circle. Now, place a scale on the plate. This scale which joins the 2 adjacent points of the bangle or plate is termed the diameter of that bangle or plate.

Diameter of a Bangle.
The concept of diameter is vital for numerous applications in arithmetic as well as in practical life also.
Diameter Symbol
The symbol used for diameter in engineering is referred to as “phi” which is written as “⌀”. This symbol is employed to indicate the diameter of a circular section; as an example, "⌀20" means that the diameter of the circle is 20 units. The other symbol of diameter used is “d”.
Formula for Diameter of a Circle
In order to calculate the diameter of a circle, we will use the formula :
d=2r
where, d is the diameter and r is the radius of the circle.
Now lets understand the concept behind this formula.
As you know that the radius of the circle is the distance between any of the points on the circumference and center. When we make 2 adjacent radii, they create a complete line and joins 2 parallel points on the circumference of the circle. This line is called the diameter.
Thus, double the value of radius is equal to the diameter of the circle.
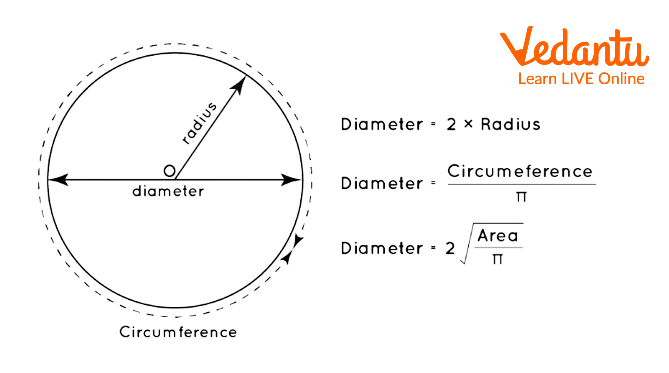
Formula for Diameter.
The different ways in which we can calculate the diameter of a circle are as follows :
If the radius of a circle is given , we will calculate the diameter of the circle as :
d=2r
where , d is the diameter of the circle and r is radius of circle.
When the circumference of the circle is given , the formula to calculate the diameter of circle is :
\[d=\frac{C}{\pi }\]
where , d is diameter , C is the circumference of circle and pi is the constant value.
When the area of the circle is given, the diameter of circle will be :
\[d=\sqrt{\frac{4A}{\pi }} \]
\[d=2\sqrt{\frac{A}{\pi }} \]
here , d is diameter of circle
A is the area of circle and pi is the contant value.
Solved Problem
Q. Caculate the diameter of the circle when the circumference of circle is 78 cm .
Ans. Given : circumference of circle , C=78 cm.
To calculate : Diameter of circle , d .
We know that , when circumference of a circle is given , the formula used is :
\[d=\frac{C}{\pi }\]
\[ d=\frac{78}{3.14} \]
\[d=24.8\text{cm} \]
Therefore , the diameter of circle is 24.8 cm.
Summary
Two-dimensional shapes have only 2 dimensions, such as length and breadth, whereas 3D shapes need three dimensions. Along with length and breadth, 3D shapes have height. The shapes are defined using completely different terms length, height, area, etc. One such parameter that defines the shape circle is “Diameter”. We can conclude that the diameter is the longest chord of the circle.
FAQs on Diameter of a Circle Explained
1. What is the diameter of a circle?
The diameter of a circle is a straight line segment that passes through the center of the circle and has its endpoints on the circle's boundary. It is the longest possible distance across a circle and is also known as the longest chord of the circle.
2. What is the relationship between the diameter and the radius of a circle?
The diameter of a circle is exactly twice the length of its radius. The radius is the distance from the center to any point on the circle's edge. Therefore, the formula connecting them is d = 2r, where 'd' is the diameter and 'r' is the radius.
3. How can you calculate a circle's diameter if you know its circumference?
You can find the diameter by dividing the circumference by the mathematical constant Pi (π). The formula is d = C / π, where 'd' is the diameter and 'C' is the circumference. This works because Pi is defined as the ratio of a circle's circumference to its diameter.
4. What is the formula to find the diameter of a circle from its area?
To find the diameter from the area, you first need to find the radius. Start with the area formula, A = πr², and solve for 'r' (r = √(A/π)). Once you have the radius, calculate the diameter using d = 2r. The combined formula is d = 2√(A/π).
5. How is the concept of a diameter used in real life? Can you give some examples?
The concept of diameter is used frequently to describe the size of round objects. Common examples include:
- The size of a pizza (e.g., a '12-inch pizza' refers to its diameter).
- The dimensions of car or bicycle wheels.
- The width of a round table or a circular swimming pool.
- In construction, to specify the size of pipes, tunnels, or columns.
6. What is the main difference between a diameter and a chord of a circle?
A chord is any straight line segment that connects two points on the edge of a circle. A diameter is a special type of chord that has one additional requirement: it must pass through the center of the circle. Because it passes through the center, the diameter is always the longest chord in a circle.
7. Why must a diameter pass through the center of the circle?
A diameter represents the widest possible distance across a circle. This maximum distance can only be achieved by a line segment that passes directly through the center point. Any other line (a chord) that does not pass through the center will be shorter because it connects points on the circle's curve that are closer together.
8. If you double the diameter of a circle, what happens to its circumference and area?
If you double the diameter of a circle:
- The circumference also doubles. This is because the circumference (C = πd) has a direct, linear relationship with the diameter.
- The area becomes four times larger. This is because the area (A = πr²) depends on the square of the radius. Since doubling the diameter also doubles the radius, the area increases by a factor of 2², which is 4.
9. Can a circle have more than one diameter?
Yes, a circle has an infinite number of diameters. Any straight line that goes through the center and connects two opposite points on the circle's edge is a diameter. While you can draw countless such lines by rotating them around the center, all diameters of the same circle will have the exact same length.
10. How would you measure the diameter of a real-world object like a plate?
To measure the diameter of a plate, you would use a ruler or measuring tape. Place the '0' mark of the ruler on one edge of the plate. Then, extend the ruler across the plate, making sure it passes over the visual center of the plate, to the opposite edge. The measurement at the opposite edge is the diameter. For accuracy, you can take a few measurements across different angles and average them.








































