




Why Understanding Decimal Place Value Matters in Maths
The place values of the digits in a decimal number are displayed on the decimal place value chart. We know that a digit in a number represents a numerical value or place value.
Decimal place value charts are used to determine the proper placement of each digit in a decimal number. The place values of the digits given before and after the decimal point are displayed.
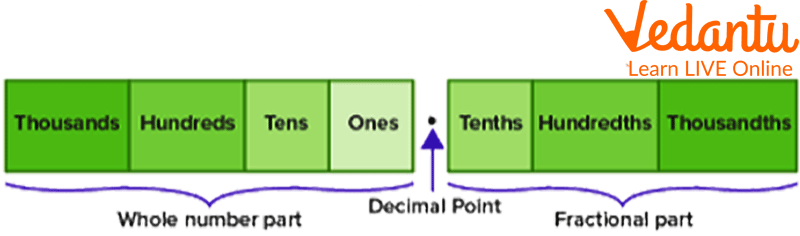
Place Value in Decimal
Place Value Definition in Decimals
A decimal number consists of a whole number and a fractional component, separated by the decimal point, a dot.
For instance, the decimal number 4.37 has two parts: an actual number portion of 4 and a fractional portion of 37. The place values of all digits are displayed in a decimal place value chart.

This is How we Deduct Values after Decimal Points.
The place values often represented by the digits preceding the decimal point are ones, tens, hundreds, thousands, and so forth. While the place values represented by the numbers after the decimal point begin with the tenth, moving up through the hundredths and thousandth.
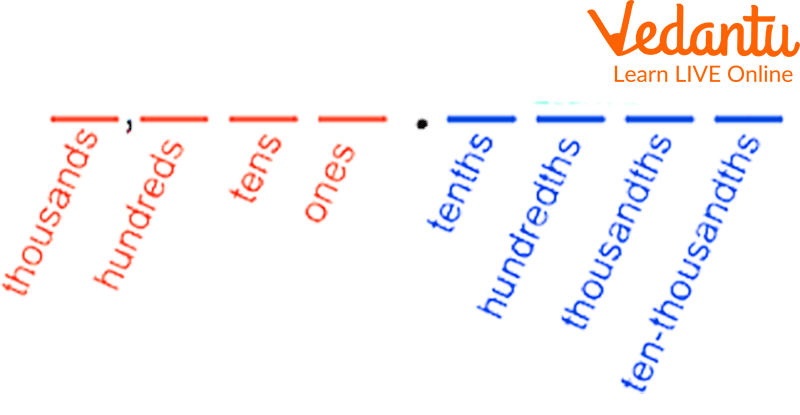
Place Value Chart
Chart of Decimal Place Values
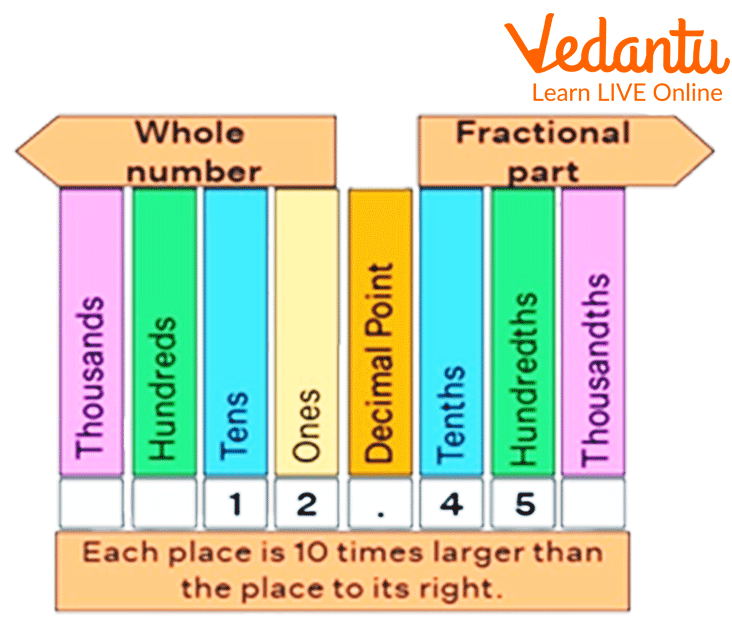
Representation of Decimal Values
The place values before the decimal point start with ones, followed by tens, and so forth, while the place values following the decimal point start from tenths, followed by hundredths, then thousandths, and so forth. The fractional portion of the number is represented by the place value that follows the decimal. The number 0.56, for instance, is composed of 5 tenths and 6 hundredths. This can be expressed as 0.56 = 0.5 + 0.06. In other terms, 0.56 is $\dfrac{5}{10} \text { plus } \dfrac{6}{100}$.
Solved Examples
1. Write the place value of the digits 2 and 4 in the number 326.471
Ans: The steps to solve this problem is as follows:
First, write the number in a decimal place value chart.
Then, look at the digit's place and find its place value.
The digit 2 is in the tens place. Therefore, its place value is 2 tens or 20.
The digit 4 is in tenth place. Therefore, its place value is four-tenths of 0.4
2. Find the place value of the underlined digits in the number 4532.079
Ans: The steps to solve this problem is as follows:
In the number 4532.079:
4 is at the thousands place. So, its place value is 4 thousands or 4000
0 is in tenth place. So, its place value is 0 tenths or 0
9 is at the thousandth place. So, its place value is 9 thousandths of 0.009
Fun Facts About Decimal Place Value
The actual value of a digit is called its face value. Unlike the place value of an integer, which depends upon its position in a number, the face value remains the same, irrespective of its class.
Have you ever been told to multiply by ten, and add zero at the end? If so, you've been misled! Here's an example: 2.3 x 10 is not 2.30. It is 23.0. When you multiply by ten, every digit shifts along with one place to the left. So, in our example, there are 2 tens rather than 2.
The 'dec' in decimal means ten and refers to the fact that each position in a decimal number corresponds to ten times more than the next. For example, the number 325.31 means 3 hundred, 2 tens, 5 ones, 3 tenths, and 1 hundredth. Humans decided to group in tens because that's how many fingers/thumbs we have. It made counting and arithmetic a whole lot easier. Three-fingered aliens might well group in threes!
Practice Questions
Q 1. Write the place value of the digits 6 and 4 in the number 926.894
Ans: 6 = ones and 4 = thousandths
Q 2. Write the place value of the digit 2 in the number 73.42
Ans: Hundredths
Summary
By adding decimal places, we can conclude that the base-10 number system may now express fractional numbers and unlimited amounts. To count parts or fractions of things, we utilize decimals. These are the numbers that appear on the number line in between the whole numbers. The decimal places are endlessly on the left and get smaller and smaller as you move along.
FAQs on Decimal Place Value Made Simple
1. What is meant by decimal place value in Maths?
In Maths, decimal place value refers to the value of each digit in a number that contains a decimal point. The decimal point separates the whole number part (on the left) from the fractional part (on the right). While the places to the left are ones, tens, hundreds, etc., the places to the right of the decimal point represent fractions and are called tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
2. How can we find the place value of each digit in the number 45.682?
To find the place value for each digit in 45.682, you can break it down as follows:
The digit 4 is in the tens place, so its value is 40.
The digit 5 is in the ones place, so its value is 5.
The digit 6 is in the tenths place, so its value is 6/10 or 0.6.
The digit 8 is in the hundredths place, so its value is 8/100 or 0.08.
The digit 2 is in the thousandths place, so its value is 2/1000 or 0.002.
3. What is the main difference between place value and face value in a decimal number?
The main difference is that face value is simply the digit itself, regardless of its position, while place value is the value it holds due to its position in the number. For example, in the number 17.47:
The face value of both 7s is just 7.
However, the place value of the first 7 is 7 (ones place), while the place value of the second 7 is 0.07 (hundredths place).
4. How does a decimal place value chart help us read numbers?
A decimal place value chart is a table that visually organizes a number's digits, making it easier to understand their value. The chart has a central column for the decimal point. To its left are columns for Ones, Tens, Hundreds, etc. To its right are columns for Tenths, Hundredths, Thousandths, etc. By placing a number like 3.14 in the chart, you can clearly see that it is composed of 3 ones, 1 tenth, and 4 hundredths, which simplifies reading and comparing decimal numbers.
5. Why is it important to understand decimal place value in real life?
Understanding decimal place value is crucial for many real-life situations. For example:
Handling Money: When you see a price like ₹25.50, you know it means 25 rupees and 50 paise (or 5 tenths of a rupee). Misunderstanding the place value could lead to financial errors.
Measurement: In science, cooking, or construction, precise measurements like 2.5 metres or 1.75 litres are common. Place value helps distinguish between 2.5 and 2.05.
Sports: Race timings, like 9.58 seconds, are measured in decimals where every hundredth of a second matters.
6. How does the value of a digit change as it moves from left to right across the decimal point?
As a digit moves from left to right, its place value becomes 10 times smaller for each position it shifts. For example, in the number 222.2:
The leftmost 2 is worth 200.
The next 2 is worth 20 (10 times smaller).
The 2 in the ones place is worth 2 (10 times smaller).
The 2 after the decimal is worth 0.2 or 2/10 (10 times smaller).
This shows a consistent pattern of division by 10 as you move right.
7. Does adding a zero at the end of a decimal number change its value?
Adding a zero at the end of a decimal number, after the last non-zero digit, does not change its value. For example, 0.8 is exactly the same as 0.80 or 0.800. This is because 8/10 is the same fraction as 80/100. However, adding a zero between the decimal point and a digit, like changing 0.8 to 0.08, does change its value significantly (from eight tenths to eight hundredths).















