




Curved Surface – Meaning and Examples
Introduction to Curved Surface
You might have various closed objects like your lunch box, water bottle, a rolled wire, and so on. What are they actually? Well, they are shapes. Now, if I ask you what you see in the image below, please mark your answer:
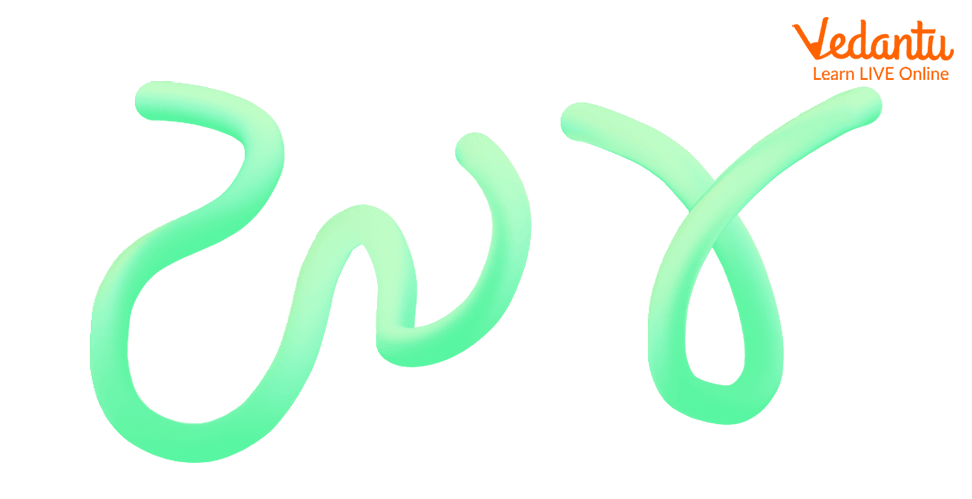
Well, these are simply wires that are rolled in different forms. However, in Maths, we call these randomly folded wires curves. So, what are curves basically? Well, a curve is an abstract term used to describe the path of a continuously moving point. We notice that these curves are made of a straight line bent to form different shapes called curves.
Now, let us understand various types of curves and also the difference in each.
Definition of a Curve
A curve is a smoothly flowing continuous line that has bent. It does not have any sharp turns. The technique to identify the curve is that the line bends and changes its direction at least once for all.
Various curve shapes other than the ones mentioned in the above image are circles, ellipses, parabolas, and hyperbolas, even arcs, sectors, and segments, they are all two-dimensional curved shapes. However, curves are three-dimensional shapes as well, such as spheres, cylinders, and cones; we all have these three-dimensional curved shapes.
Different Types of Curves
Curves are categorised into different forms. Let us have a look at different types of curves with their representations:
Simple Curve
A curve that changes its direction and does not intersect itself is a simple curve. A simple curve may be open or closed. This is what it looks like:

Non-Simple Curve
A type of curve other than a simple curve that crosses its path is a non-simple curve. It means the curve intersects itself while altering its direction. This is what it looks like:

Open Curve
A curve that has two endpoints and does not enclose the area within itself is known as an open curve. Some of the examples of open curves are shown below:

Closed Curve
A curve that has no endpoints and when it encloses the region an area forms, such a type of curve is known as the closed curve. A closed curve is formed by joining the two endpoints of the open curve. The best example of such types of curves are circles, ellipses, etc.

Curved Line
A bent line is called a curved line. If the curvature is not zero, we consider it a curve line, which is generally smooth and continuous.
Curved Line Images
We observe many objects in our surroundings that are in the shape of a curved line. Some of them incorporate the following:
Railways at the turning points,
Track of a roller coaster,
Paths of roads in hilly areas, and so on.
Apart from the real-life examples, we can also observe the curve-shaped lines in Maths; for example, the graph of a quadratic polynomial including parabola, ogive curve, arrows, etc.
So, this is how we understand curve Maths and the types of curves we find in our surroundings.
FAQs on Curved Surface
1. What is a curved surface in geometry?
A curved surface is a surface of an object that is not flat but bends in a smooth, continuous way. Think of the outside of a ball, the side of a soda can, or the surface of a globe. Unlike a flat surface where you can lay a ruler flat in any direction, a curved surface has at least one direction where it bends or deviates from a straight plane.
2. What are some common examples of objects with curved surfaces?
Many everyday objects have curved surfaces. Common examples include:
- The surface of a football or cricket ball (sphere)
- The label area of a tin can or battery (cylinder)
- The slanting part of an ice cream cone or a birthday hat (cone)
- The outer shell of an egg
- The lens of a magnifying glass or spectacles
3. What is the main difference between a flat surface and a curved surface?
The key difference is that a flat surface, like a tabletop, has zero curvature; you can place a straight ruler anywhere on it and it will lie perfectly flat. A curved surface, however, has a non-zero curvature. A ruler placed on it will only touch at one or two points, rocking back and forth unless placed along a specific straight line (which is only possible on certain curved surfaces like a cylinder's side).
4. Which 3D shapes are known for having curved surfaces?
In geometry, several fundamental 3D shapes are defined by their curved surfaces. The most common ones students learn about are:
- Sphere: An object where every point on its surface is equidistant from the center. It consists of a single, continuous curved surface.
- Cylinder: A shape with two identical flat, circular bases and one curved side connecting them.
- Cone: A shape with one flat, circular base and a single curved surface that tapers to a point (vertex).
5. Why is it important to distinguish between flat and curved surfaces in Maths?
Understanding the difference is critical for calculating geometric properties, especially surface area and volume. The formulas and methods used for flat-surfaced objects (like cubes and cuboids) are based on linear dimensions (length, width, height). In contrast, calculating the surface area of curved objects requires different formulas involving constants like pi (π) and radius (r), reflecting their non-linear nature.
6. Can a single object have both flat and curved surfaces?
Yes, many common 3D objects are composite shapes that feature both flat and curved surfaces. A perfect example is a cylinder, which has two flat circular bases and one continuous curved side. Similarly, a cone combines one flat circular base with one curved surface. A hemisphere (half a sphere) also has one flat circular surface and one curved surface.
7. How is the area of a curved surface measured differently from a flat one?
You cannot measure the area of a curved surface using a simple length × width formula. The concept often involves imagining the surface being 'unrolled' into a standard flat shape. For instance, the curved surface of a cylinder can be conceptually 'unrolled' to form a rectangle, making its area easy to calculate. For shapes like a sphere, which cannot be flattened without distortion, specific formulas derived through advanced mathematics are used, such as 4πr².
8. What are the different types of curves?
In mathematics, a curve is a continuous line that bends without sharp turns. They are generally classified based on their properties:
- Simple Curve: A curve that does not cross over itself (e.g., a circle, a parabola).
- Non-Simple Curve: A curve that intersects its own path (e.g., a figure-eight).
- Open Curve: A curve with two distinct endpoints that do not meet (e.g., the letter 'S').
- Closed Curve: A curve with no endpoints that encloses a region (e.g., a circle, an ellipse).





















