




How to Find Tangency Condition for Parabola Problems
We all have seen and solved an equation of a parabola and understand the basic concept of a parabola in the conic section. A tangent to parabola is only possible when the condition of tangency is satisfied. Different type of parabola has a different condition of tangency. To find the condition of tangency of a general parabola with a vertex other than the origin, one needs to solve the equation of tangent and parabola and try to eliminate the variable, and use the discriminant rule \[{b}^{2}=4ac\].
In this article, we will understand the concept of a tangent to a parabola. Condition of tangency to a parabola. Solve some questions regarding the tangency condition of different parabola forms.
Different Types of Parabolas and Their Graphical Representation
There are several types of parabolas. The first type of parabola is when the origin of the parabola is at the origin $(0,0)$, and the other type will be the general parabola, where the centre of the parabola is anywhere.
Upward parabola (Faces upward)
Downward parabola (Faces downward)
Right parabola (Faces right)
Left parabola (Faces left)
General parabola
Starting with the common standard upward parabola, The equation of an upward parabola is ${{x}^{2}}=4ay$, where $a$ is the distance of focus from the origin. The graph of the upward parabola is as follows,
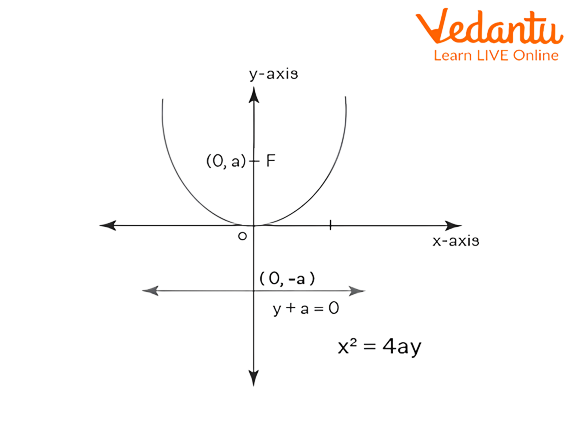
Graphical representation of upward parabola.
The equation of the right parabola is ${{y}^{2}}=4ax$. The graph of the upward parabola is as follows,
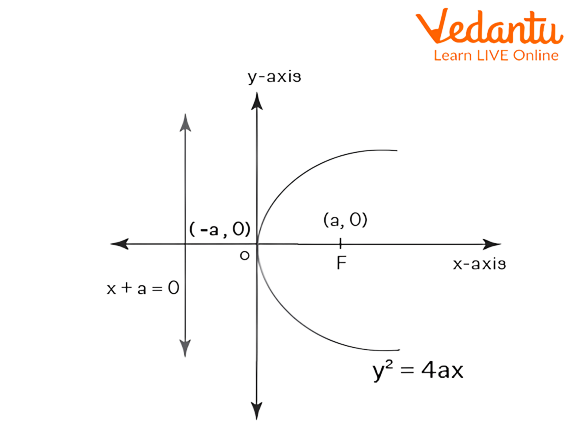
Graphical representation of the right parabola.
The equation of the left parabola is ${{y}^{2}}=-4ax$. The graph of the upward parabola is as follows,
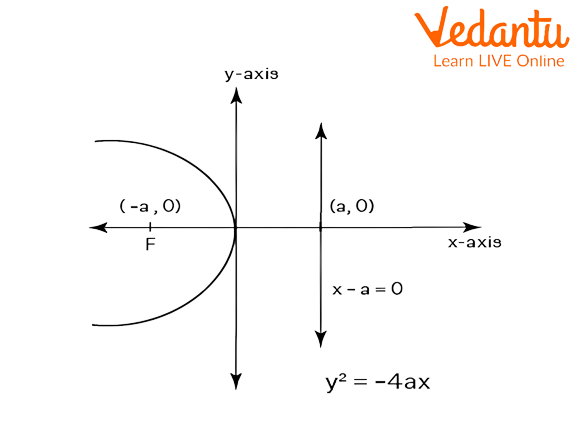
Graphical representation of the left parabola.
The equation of left parabola is ${{x}^{2}}=-4ay$. The graph of the downward parabola is as follows,
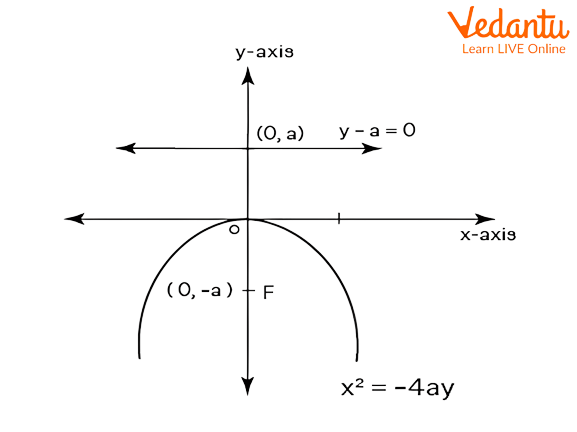
Graphical representation of downward parabola.
The equation parabola at centre $(h,k)$ will be $y=a{{(x-h)}^{2}}+k$.
Condition of Tangency of a Parabola
To draw a tangent to a parabola, one must need to follow the condition of tangency to draw the tangent to a parabola. There are three types of conditions that must be followed to find the tangent to a parabola, specifically for right, upward and parametric forms.
The condition of tangency are as follows:
The line $y=mx+c$ is a tangent to a parabola ${{y}^{2}}=4ax$ only if $c=\dfrac{a}{m}$.
The line \[y=mx+c\] is a tangent to a parabola ${{x}^{2}}=4ay$ only if $c=-a{{m}^{2}}$.
The line $x\cos \theta +y\sin \theta =p$ is a tangent to a parabola ${{y}^{2}}=4ax$ only if $\sin 2\theta +p\cos \theta =0$.
Equation of Tangent to a Parabola
If the equation of a parabola is given in the standard form. Then, the equation of a tangent to parabola can be easily found by following the given steps:
First, you need to find the point of intersection of the parabola and tangent and the slope of the tangent.
The slope of the tangent is given by differentiating the equation of the parabola and putting the point of intersection on the derivative.
Then, use the point-slope form of a line to write the equation of tangent.
Example: Write the equation tangent to a parabola with equation ${{y}^{2}}=16x$ at $(1,4)$.
Solution: Comparing the equation of the parabola with the standard equation and differentiating the equation to get the slope of the line:
By comparing the equation with the standard equation, we get
${{y}^{2}}=4\times 4x$
$a=4$
Differentiating the curve equation, $\dfrac{d({{y}^{2}})}{dx}=\dfrac{d(16x)}{dx} $
$2y\dfrac{dy}{dx}=16 $
$\dfrac{dy}{dx}=\dfrac{8}{y} $
${{\dfrac{dy}{dx}}_{(1,4)}}=\dfrac{8}{4} $
$ m=2 $
Now, using the condition of tangency of the parabola,
$c=\dfrac{a}{m}$
$ c=\dfrac{4}{2}$
$c=2$
So, the equation of tangent to parabola is $y=2x+2$.
Point of Contact of Tangent and Parabola
The point of contact between the tangent and parabola is a point where the tangent and curve meet each other. The point of contact is easily given by following some basic steps:
First, you have to solve the tangent equation and a parabola equation.
The value of x and y is the point of contact.
The point of contact of tangent $y=mx+\dfrac{a}{m}$ right parabola ${y}^{2}=4ax$is $\left( \dfrac{a}{{{m}^{2}}},\dfrac{2a}{m} \right)$.
The point of contact of tangent $y=mx-a{{m}^{2}}$ right parabola ${{x}^{2}}=4ay$ is $\left( 2am,a{{m}^{2}} \right)$.
Where $a$ is the length of focus and $m$ is the slope of the tangent.
Example: Verify the condition of tangency and find the point of contact of tangent $3x+4y=5$ to a parabola $80y=-9{{x}^{2}}$.
Solution: First, verify the condition of tangency and then find the point of contact:
Finding the value of $a$,
$9{{x}^{2}}=-80y$
${{x}^{2}}=-\dfrac{80}{9}y$
${{x}^{2}}=-4\times \dfrac{20}{9}y$
Hence, the value of $a$ is $\dfrac{20}{9}$.
Now, finding the intercept and slope of the given tangent by writing it in slope-intercept form,
$3x+4y=5$
$4y=-3x+5$
$ y=-\dfrac{3}{4}x+\dfrac{5}{4}$
Hence, the slope of the tangent is $-\dfrac{3}{4}$ and the intercept is $\dfrac{5}{4}$.
The condition of tangency is \[c=a{{m}^{2}}\], putting the values.
$\dfrac{5}{4}=\dfrac{20}{9}\times {{\left( -\dfrac{3}{4} \right)}^{2}}$
$ \dfrac{5}{4}=\dfrac{20}{9}\times \dfrac{9}{16}$
$\dfrac{5}{4}=\dfrac{5}{4}$
Hence, the condition of tangency is verified.
Now, the point of contact of a tangent to the parabola is given as $(2am,am^2)$. Putting the values,
$\left( 2\times -\dfrac{20}{9}\times -\dfrac{3}{4},-\dfrac{20}{9}{{\left( -\dfrac{3}{4} \right)}^{2}} \right)=\left( \dfrac{10}{3},-\dfrac{5}{4} \right)$
Hence, the point of contact of the parabola and tangent is $\left( \dfrac{10}{3},-\dfrac{5}{4} \right)$.
Solved Problems
Q.1 Prove that the line $y-2x+28=0$ is a tangent to parabola $x=14t;y=7{{t}^{2}}$.
Ans. Given: The parametric equation of a parabola is $x=14t;y=7{{t}^{2}}$, and the equation of tangent is $y-2x+28=0$.
To prove the condition of tangency.
By looking at the parabola equation, it is clear that the parabola is upward.
We know that the condition of tangency of the upward parabola is $c=-a{{m}^{2}}$.
By comparing the equation of a parabola with standard equation $x=2at;y=a{{t}^{2}}$, we get
$a=7$
By comparing the equation of tangent with the slope-intercept form of the line, we get
$y-2x+28=0$
$ y=2x-28$
$m=2$
$c=-28$
Now, putting the values in the condition of tangency,
$c=-a{{m}^{2}}$
$-28=-7\times {{(2)}^{2}}$
$-28=-7\times 4$
$28=28$
Hence, the condition of tangency is satisfied. The line is tangent to the given parabola.
Q.2 Find the point of contact of tangent $y=5x+\dfrac{4}{5}$ to a parabola ${{y}^{2}}=20x$.
Ans. Given: The equation of parabola is ${{y}^{2}}=20x$ and the equation of tangent is $y=5x+\dfrac{4}{5}$.
To find The point of contact of tangent and parabola.
The point of contact of the tangent to a parabola is given by $\left( \dfrac{a}{{{m}^{2}}},\dfrac{2a}{m} \right)$.
By comparing the equations with standard forms, we get
$a=4$
$m=5$
Putting the values in standard point of contact,
$\dfrac{a}{{{m}^{2}}},\dfrac{2a}{m}=\dfrac{4}{{{5}^{2}}},\dfrac{2(4)}{5}= \dfrac{4}{25},\dfrac{8}{5} $
Hence, the point of contact of tangent and parabola is $\left( \dfrac{4}{25},\dfrac{8}{5} \right)$.
Summary
The tangent to a parabola is a line intersecting the parabola exactly once. The tangent to a parabola must be drawn per the tangency condition. The condition of tangency for a right parabola is that the intercept of the tangent line must be equal to the ratio of focal distance and the slope of the tangent.
The tangent $y=mx+c$ to a parabola with equation ${{y}^{2}}=4ax$ is only possible when $c=\dfrac{a}{m}$. The tangent $=mx+c$ to a parabola with equation ${{x}^{2}}=4ay$ is only possible when $c=-a{{m}^{2}}$. In this article, we have learned the condition of the tendency of the parabola.
Practice Questions
1. Verify the condition of tangency for parabola \[y=36{{x}^{2}}\] and the tangent \[y+9=x\].
Ans. The condition can be verified by finding the value of slope and focal distance.
2. Find the equation of tangent with slope equal to $7$, to a parabola \[y=4{{x}^{2}}\].
Ans. $y=7x-49$
List of Related Articles
FAQs on Condition of Tangency in Parabola Explained
1. What is the primary condition for a line to be tangent to a standard parabola y² = 4ax?
For the standard parabola y² = 4ax, a line with the equation y = mx + c is considered a tangent if and only if it satisfies the condition c = a/m. This means the y-intercept 'c' of the line must be precisely equal to the ratio of the parabola's parameter 'a' to the line's slope 'm'.
2. How is the condition of tangency for a parabola derived using the discriminant method?
The condition of tangency is derived by solving the line's equation (y = mx + c) and the parabola's equation (y² = 4ax) simultaneously. This leads to a quadratic equation in 'x'. For the line to be a tangent, it must touch the parabola at exactly one point. This requires the quadratic equation to have exactly one real root, which happens when its discriminant (D) is zero. Setting D = 0 for the resulting equation, (mx + c)² = 4ax, and solving for 'c' gives the fundamental condition c = a/m.
3. What are the three main forms of the equation of a tangent to the parabola y² = 4ax?
The equation of a tangent to the parabola y² = 4ax can be written in three key forms based on the given information:
Point Form: If the point of tangency is (x₁, y₁), the equation is yy₁ = 2a(x + x₁).
Parametric Form: For a point with parameter 't', i.e., (at², 2at), the equation is ty = x + at².
Slope Form: For a tangent with a given slope 'm', the equation is y = mx + a/m.
4. How does the condition of tangency change for other standard parabola orientations?
The condition of tangency for the line y = mx + c depends on the parabola's specific equation. The main variations are:
For the parabola y² = -4ax, the condition is c = -a/m.
For the parabola x² = 4ay, the condition is c = -am².
For the parabola x² = -4ay, the condition is c = am².
5. Why is the parametric form of a tangent so important in solving problems?
The parametric form, ty = x + at², is highly significant because it expresses both the coordinates of any point on the parabola and the equation of the tangent at that point using a single variable 't'. This simplifies complex problems, such as finding the locus of the intersection of tangents or normals, by reducing the number of variables (x, y) to one, making algebraic manipulation much more manageable.
6. What is the equation of the tangent to a standard parabola at its vertex?
The tangent at the vertex of a parabola is always the axis that is perpendicular to the parabola's own axis of symmetry. For the standard parabola y² = 4ax, the vertex is at the origin (0, 0) and the axis of symmetry is the X-axis. Therefore, the tangent at the vertex is the Y-axis, and its equation is x = 0.
7. Can a straight line be tangent to a parabola at two distinct points?
No, a straight line cannot be tangent to a parabola at two distinct points. By definition, a tangent touches the curve at a single point without crossing it at that point. A line that intersects a parabola at two distinct points is called a secant, not a tangent. The condition for tangency itself is derived from the requirement that the line and parabola have only one point of intersection.















