Area of Sector and Segment of a Circle

The region between two radii of a circle and any of the arcs between them is called a sector. The sector always starts from the center of the circle. The semi-circle is also called the sector of the circle. The space or the area occupied by the sector of a circle is called the area of a sector of a circle. Geometrically, a line segment is a part of a line that is bounded by two distinct end points, and contains every point on the line between its endpoints.

Area of Sector Definition

A sector of a circle is identified as the reconstructed part of the circle bounded by two radii and the arc which connects them. The space which is occupied by the sector of a circle is called the area of a sector of a circle.

Two types of sectors are major sectors and minor sectors.

• A major sector is defined as a sector that is greater than a semicircle.

• A minor sector is defined as a sector that is less than a semi-circle.

As the below image represents the minor and major sectors. Hence, the shaded part OAPB is the area of the minor sector, whereas the unshaded part OAQB is the area of the major sector of the original circle.

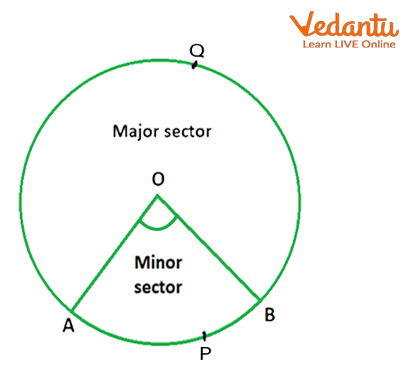
Area of a Sector of a Circle

Real-Life Example for Sector of a Circle

The most common real-time example of a sector is a slice of pizza. The shape of the slices of pizza is similar to a sector of a circle.

The pizza of 7 inches is equally divided into 6 equal-sized slices, with each at an angle of 60 degrees, as shown in the below image.

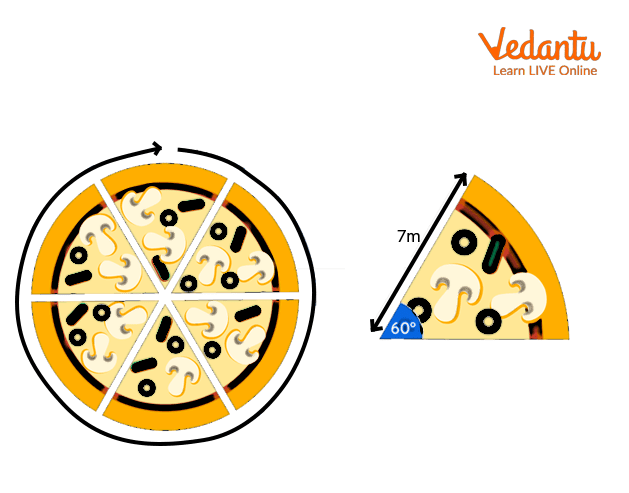
Example for the Sector.

In this image, the pizza slice is a representation of the sector, and these 6 slices are the 6 equal sectors.

The Area of the Sector of a Circle Formula

This formula can be used to calculate the total space covered by a part of a circle. The area can be calculated as the total space covered by a circle. The area can be calculated in two different ways with respect to the unit of an angle given.

This is the formula for calculating the area of a sector of a circle.

• $\text{Area of sector of a circle =}\frac{\theta }{{{360}^{\circ }}}\times \pi {{r}^{2}}$

• Where r is the radius of the circle and θ is the angle subtended at the center.

A Segment of a Circle Definition

• A segment in a circle is an area that covers the chord and an arc of the circle.

• The chord is a line segment that joins any two points on the circumference of the circle.

• An arc is a portion of a circle or a segment of the perimeter of the circle.

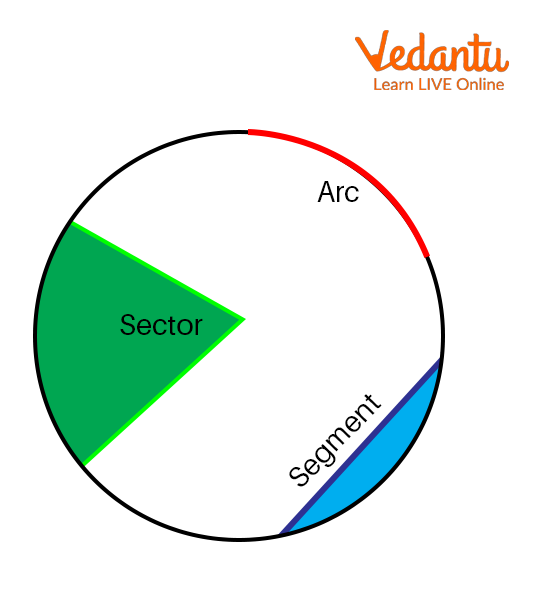
Segment of a Circle.

There are two types of segments.

1. Major segment

2. Minor segment

A major segment is made from the major arc. A minor segment is made from the minor arc.

Area of a Segment of a Circle

The area of a segment of a circle is correspondingly equal to the area of the sector subtracted by the area of the triangle.

The Area of a Segment of the Circle Formula

In the below figure, a triangle OPQ is given considering it as a minor segment made by the chord PQ of the circular with a given radius r. As we know from trigonometry the area of triangle OPQ is $\frac{1}{2}\times {{r}^{2}}\times \sin \theta$ .

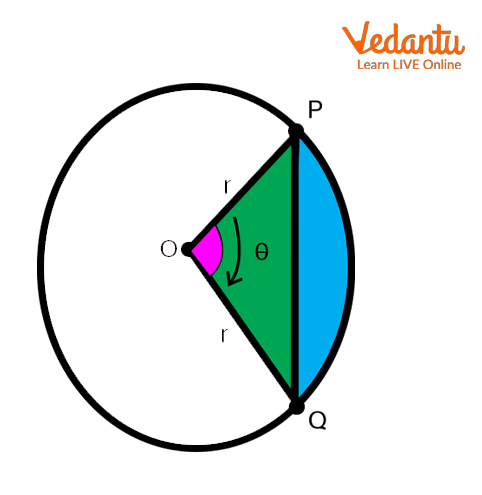
Area of a Segment.

The area of the sector OPQ is given by

1. $Area=\frac{\theta }{360}\times \pi {{r}^{2}}$ if θ is in degrees.

2. $Area=\frac{1}{2}\times {{r}^{2}}\times \theta$ if θ is in radians.

Therefore, to calculate the formulas, the area of the minor segment of the circle is :

1. When θ is in degree ,

$ \text{Area of sector= }\frac{\theta }{360}\pi {{r}^{2}} $

$\text{ Area of segment = }\frac{\theta }{360}\pi {{r}^{2}}-\frac{1}{2}\text{ }{{\text{r}}^{2}}\text{ sin}\theta \text{ } $

$ \text{=}{{r}^{2}}\left( \frac{\theta }{360}\pi -\frac{1}{2}\sin \theta \right) $

2. When θ is given radians,

$ \text{Area of sector=}\frac{1}{2}{{r}^{2}}\theta $

$ \text{Area of segment =}\frac{1}{2}{{r}^{2}}\theta -\frac{1}{2}{{r}^{2}}\sin \theta $

$ =\frac{1}{2}{{r}^{2}}\left( \theta -\sin \theta \right) $

Theorems on Segments of a Circle

Basically, there are two theorems that are based on the segment of a circle.

• Angles in the same Segment Theorem

The first theorem states that the angle formed in the same circle segment is always equal.

• Alternate Segment Theorem

The second theorem of segments states that the angle formed by the tangent and chord at the point of contact equals the angle formed in the alternate segments on the circle circumference at the chord endpoints.

Solved Examples

1. RQRQ is a chord of a circle that subtends an angle of 80∘ at the centre of a circle, and the diameter of the circle is 15cm. Calculate the area of the minor sector of this circle.

Solution: The diameter of the circle =15 cm.

The radius of the circle = $15\div 2=7.5cm$

Using the formula of the area of a sector of the circle

$ \text{Area of minor sector=}\frac{\theta }{360}\times \pi {{r}^{2}} $

$ =\frac{80}{360}\times \frac{22}{7}\times {{\left( 7.5 \right)}^{2}} $

$ =39.25c{{m}^{2}} $

Therefore, the area of the minor sector is 39.25cm2.

2. Calculate the area of the major segment of a circle if the area of its minor segment is 62 sq. units and the radius is 7 units. Use π= 22/7.

Solution: Using the relation,

area of the major segment = area of the circle − the area of the minor segment

$ \text{Area of major segment =}\pi {{r}^{2}}-62 $

$ \text{=}\frac{22}{7}{{\left( 7 \right)}^{2}}-62 $

$ =154-62 $

$ =92sq.unit. $

Therefore, the area of the major segment is 92 sq. units.

Summary

In this article, we discussed the sector and segment. The relevant problems in sector and segment are taken as example problems to solve sector and segment, which include the area of a segment of a circle and the area of the sector of a circle and their respective formulas.