




Step-by-Step Guide to Adding and Subtracting Multi-Digit Numbers
Everyone learns to count numbers at a young age, beginning with a single digit and progressing to seven digits. Adding and subtracting larger numbers is an easy maths problem that everyone can do. It involves adding or subtracting the value of one number from another. The problem is that we often write “1+1=2” without considering the actual number.
We add large numbers the same way we add other numbers. The integers are arranged in a column based on their place values. The addition procedure starts with the one's column, then moves on to the tens column, then the hundreds column, and so on. For subtraction, we do the same. This article will teach us about the place value addition and subtraction of larger numbers.
International Place Value Chart
The International Numerical System includes tens, hundreds, thousands, ten thousand, hundred thousand, millions, etc. This can be understood from the image shown below.
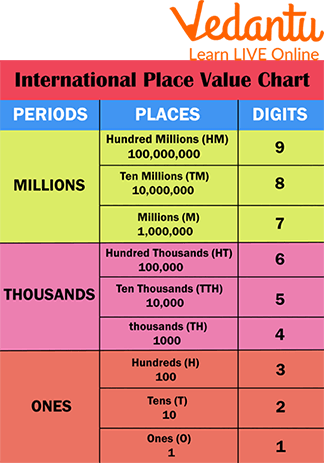
International Place Value Chart
Indian Place Value Chart
The Indian place value chart is a table that is used to find the value of each digit in a number based on its position, as per the Indian Numeral System. The place value of a number shows how much a digit is worth based on its position. In order to avoid confusion while reading very large numbers, we arrange the numbers into periods with the help of a comma as the separator.
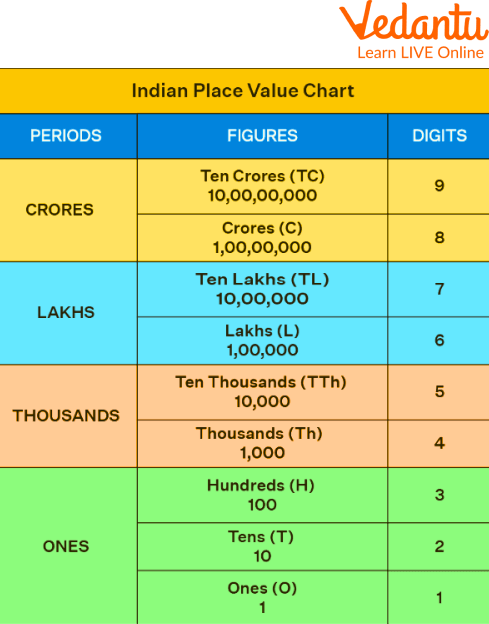
Indian Place Value Chart
Relationship Between Place Values
The place value of digits in numbers can also be represented using base-ten blocks and can help us write numbers in their expanded form.
The hundreds place is one position to the left of the tens place and is 10 times bigger than the tens place.
When we move one spot to the left side from the ones place, the tens place becomes 10 times greater than the ones place.
The thousands place is 10 times bigger than the hundreds place when we go from one spot to the left side from the hundreds place.

Place Value Relationship
Now observe that the value of the base 10 blocks on the far left is 3,000. The value of the blocks decreases by a factor of ten each time we walk to the right. The 3, therefore, has a value that is a tenth that of the earlier number.

Place Value Relationship
Place Value Addition and Subtraction
The addition procedure starts with the one's column, moves on to the tens column, then the hundreds column, and so on. The numbers that must be carried forward are inserted alongside the existing numbers in the adjacent column. This process must be repeated until we reach the last column and obtain our final number.
The same column order used for addition is used for large-number subtraction. Once the numbers are in the columns, we start with one and work our way to the left. Numbers are borrowed from the left side when needed.
Adding and Subtracting with Regrouping
Regrouping happens whenever a column's sum is greater than 9. If any digit in the minuend is less than the corresponding digit in the subtrahend, regrouping is performed in subtraction. Before learning about subtraction with regrouping, let's first study addition with regrouping.
Regrouping During Subtracting
Any time a digit in the minuend is smaller than the equivalent digit in the subtrahend, subtraction with regrouping is performed. To make the minuend digit greater than the subtrahend digit, we borrow 1 from the column before and add it to this minuend.
Regrouping When Adding
In addition to regrouping, when a total in any of the columns is greater than 9, we take the extra digit over to the column before it and add it together with the addends.
Solved Examples of Adding and Subtracting Larger Numbers
Here, a few examples related to adding and subtracting larger numbers have been described.
Examples: Perform subtraction of the numbers 432 - 256.
Ans: Let's subtract these integers using the borrow method.
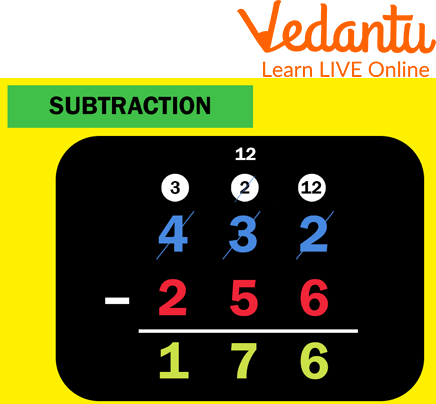
Subtraction
Example: Find the sum of 355 and 466.
Ans: The sum of 355 and 466 is 821.

Addition
Worksheet: Adding and Subtracting Larger Numbers
Here is a worksheet related to adding and subtracting larger numbers for practice.

Worksheet on the Addition of Three-digit Numbers
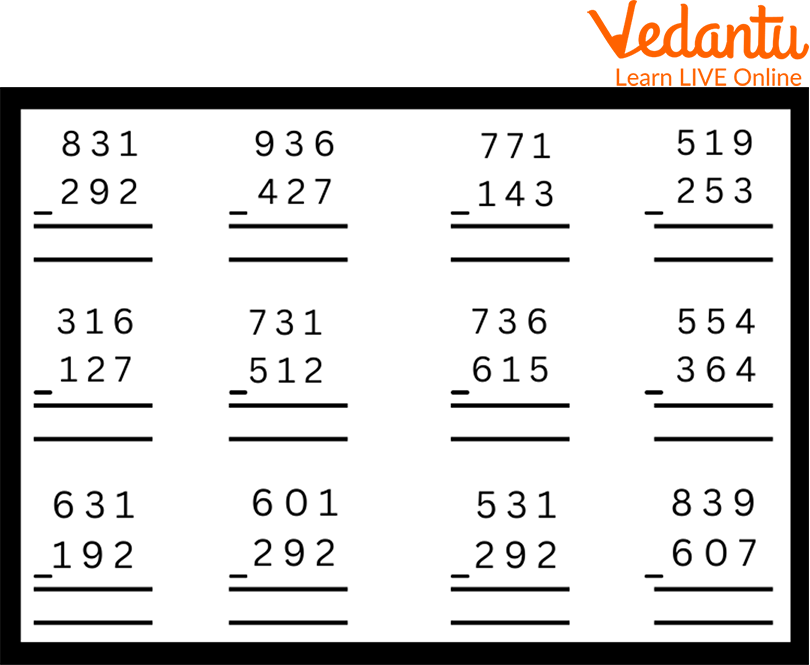
Worksheet on Subtraction of Three-digit
Summary
Numbers are a very important part of our lives. They are used in all sorts of things, from buying products to having a job. In this article, we have learned how we can add and subtract larger numbers. We must take care of the place value system for adding and subtracting larger numbers. Like ones will be added to ones first and the same case in subtraction. If we follow this, it can be easily done without any mistakes, even if the number is too large. We hope this article will help you to learn about adding and subtracting larger numbers. We have added the worksheet, do give it a try once you go through the article.
FAQs on Adding and Subtracting Larger Numbers Made Simple
1. What is the correct method for adding large numbers?
To correctly add large numbers, you should follow a systematic, step-by-step process. The key is to work with each place value column individually. The method is as follows:
Align the numbers: Write the numbers one below the other, carefully aligning the digits according to their place value (ones under ones, tens under tens, hundreds under hundreds, and so on).
Start from the right: Always begin adding with the digits in the rightmost column (the ones place).
Add and carry over: Add the digits in the first column. If the sum is 9 or less, write it below. If the sum is 10 or more, write the last digit of the sum below and carry over the other digit to the top of the next column to the left.
Repeat for all columns: Continue this process, moving from right to left, column by column, until you have added all the digits.
2. How do you subtract large numbers, especially when you need to borrow?
Subtracting large numbers involves a method called regrouping or borrowing. Here are the steps:
Position the numbers: Place the larger number on top of the smaller number. Ensure all digits are aligned by their place value.
Subtract from right to left: Start with the ones column. If the top digit is larger than the bottom digit, subtract normally.
Borrow when necessary: If the top digit in a column is smaller than the bottom digit, you must 'borrow' from the next place value column to its left. Reduce the digit in the column to the left by 1, and add 10 to the digit you are currently working on. Then, perform the subtraction.
Continue across: Repeat this process for each column, moving from right to left, until the entire subtraction is complete.
3. What are some real-world examples of adding and subtracting large numbers?
Adding and subtracting large numbers is a crucial skill used in many real-world situations. For example:
Finance and Banking: Calculating the total money in a bank account after deposits (addition) and withdrawals (subtraction).
Population Statistics: Finding the total population of a city by adding up people in different areas, or calculating population change by subtracting deaths from births.
Inventory Management: Businesses add new stock to their inventory count and subtract items that have been sold to know how much is left.
Budgeting: Calculating total monthly expenses (addition) and finding out the remaining money from a salary (subtraction).
4. Why is aligning numbers by place value so important when adding or subtracting?
Aligning numbers by place value is the most critical step because our number system is based on it. Each digit in a number has a specific value based on its position (ones, tens, hundreds, etc.). If you don't align them correctly, you end up adding or subtracting digits of different values—for example, adding a 'ten' to a 'hundred'. This fundamentally breaks the logic of the calculation and will always lead to an incorrect answer. Correct alignment ensures you are combining values of the same type.
5. What does it mean to 'carry over' in addition, and how does it work?
The 'carry-over' in addition is a shortcut for regrouping values into the next highest place value. When the sum of digits in any column is 10 or more, it means you have enough to form one or more units of the next place value. For example, if you add 8 and 7 in the ones column, you get 15. This is equivalent to 1 ten and 5 ones. So, you write the '5' in the ones place of the answer and 'carry over' the '1' to be added with the other digits in the tens column. It’s how we handle sums that are too large for a single column.
6. How can you check if your answer to a large subtraction problem is correct?
You can easily check your subtraction answer by using the inverse operation, which is addition. If you calculated that A - B = C, you can verify it by adding your result (C) to the number you subtracted (B). The sum should be the number you started with (A). For example, if you calculated 5,400 - 1,200 = 4,200, you can check it by adding 4,200 + 1,200. The result is 5,400, which confirms your original subtraction was correct.















