




Stepwise Derivation of Torricelli’s Theorem Using Bernoulli’s Principle
Torricelli’s theorem is a fundamental principle in fluid mechanics describing the velocity of liquid flowing out from a hole in a tank under gravity. It is derived from Bernoulli’s theorem and is often used in JEE Main Physics for numerical and conceptual questions. This law is essential for understanding real-life phenomena like the jet from a water tank and finds direct application in scoring exam problems. Vedantu’s concise guide here will clarify the derivation, applications, and common missteps in using Torricelli’s theorem for competitive physics.
Torricelli’s Theorem: Statement and Definition
Torricelli’s theorem states that *the speed (v) with which a liquid escapes from an orifice at depth h beneath a free surface (open to atmosphere) is equal to that acquired by a body falling freely through vertical distance h under gravity.*
Mathematically, the theorem is written as: v = √(2gh), where g is acceleration due to gravity and h is the vertical height of liquid above the orifice.
Derivation of Torricelli’s Theorem Using Bernoulli’s Equation
Let’s derive Torricelli’s law step by step for JEE Main using Bernoulli’s theorem. Assume a large tank filled with liquid, with a small opening at depth h below the surface. The top surface is open to atmospheric pressure, and liquid density is ρ. Let the velocity at surface be negligible (since tank is large) compared to the velocity from the orifice.
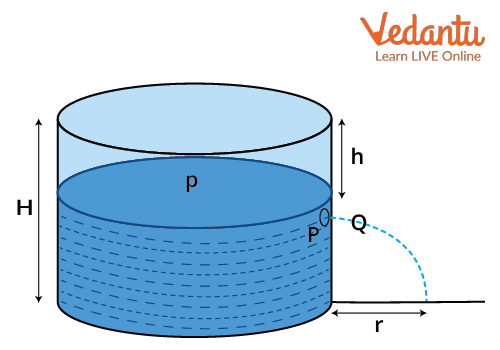
Apply Bernoulli’s theorem between liquid surface (point A) and hole at depth h (point B):
- At A: Pressure = atmospheric (Patm), velocity ≈ 0, height = h
- At B: Pressure = atmospheric (Patm), velocity = v, height = 0
Bernoulli’s equation:
Patm + ρgh + ½ρ(0)² = Patm + ρg(0) + ½ρv²
Cancel Patm terms and rearrange:
- ρgh = ½ρv²
- h = v² / (2g)
- So, v = √(2gh)
Here, h is the vertical height from the free liquid surface to the center of the orifice, and v is the efflux velocity just outside the opening.
Understanding Torricelli’s Experiment
Torricelli designed an experiment with a vessel filled with liquid and a hole at a certain depth. He observed that the stream’s speed matched what a ball would acquire falling freely through the same height, thus confirming the theory. This simple setup forms the benchmark for many JEE and practical physics demonstrations.
- Large tank partially filled with liquid (usually water or mercury)
- Small orifice at depth h below the free surface
- Measure the speed of outgoing jet and compare with theoretical value √(2gh)
- Confirmed that a freely falling body and liquid jet from the same height have equal speeds
Formula, Units, and Meaning in Torricelli’s Theorem
The efflux velocity formula is v = √(2gh). Unit of v is m/s, g is 9.8 m/s2, and h is in meters. This formula is strictly valid for non-viscous, incompressible, steady fluids with the orifice in the side or bottom of a vessel and open to air.
| Symbol | Physical Quantity | SI Unit |
|---|---|---|
| v | Speed of efflux | m/s |
| g | Acceleration due to gravity | m/s2 |
| h | Height of liquid column | m |
Applications and Sample Numericals Using Torricelli’s Theorem
Common JEE questions around Torricelli’s law ask for speed or range of emitted liquid or analyze the flow rate for practical cases. Here are real-life applications and a standard solved example:
- Water jets from tanks and fountains
- Design of reservoirs and overflow pipes
- Spillways in dams and irrigation channels
- Laboratory measurements in fluid mechanics experiments
- Predicting drain times for tanks with a bottom/side hole
- Understanding capillary action runoff with efflux scenarios
Example: A tank has water to a height of 2.5 m above a small hole. Calculate the velocity with which water exits.
- Given: h = 2.5 m, g = 9.8 m/s2
- v = √(2gh) = √(2 × 9.8 × 2.5) = √49 = 7.0 m/s
- Equations of motion confirm this consistency
Torricelli’s Theorem vs. Bernoulli’s Theorem
Torricelli’s theorem is a direct application of Bernoulli’s theorem under specific conditions. The table below highlights the difference for JEE Main clarity:
| Torricelli’s Theorem | Bernoulli’s Theorem |
|---|---|
| Gives speed of fluid outflow from orifice | Relates pressure, velocity, and height for flowing fluids |
| Special case for stationary liquid tanks | General law for any streamline in ideal fluid |
| Formula: v = √(2gh) | Formula: P + ½ρv² + ρgh = constant |
- Use Torricelli’s theorem when asked about efflux/jet speed from a tank
- Use Bernoulli’s theorem for energy/pressure balance in any steady fluid flow
Common Mistakes and Quick Revision Tips
JEE candidates sometimes forget to measure height h vertically or neglect velocity at the liquid surface when the tank cross-section is not large. The theorem is valid for non-viscous, incompressible fluids only. Always ensure the orifice faces into the atmosphere and is small compared to the tank size.
- Always take h as the vertical depth from the free surface, not slant height
- Do not use Torricelli’s theorem for viscous or compressible fluids
- Neglect surface velocity only if tank is very large
- If the orifice is not at the bottom, use correct h
Review related topics like hydrostatics, viscous forces, and surface tension for advanced challenges.
JEE Main Focus: Why Torricelli’s Theorem Matters
Strong command of Torricelli’s theorem helps tackle both direct formula numericals and theoretical questions connecting fluid dynamics with real-world cases. Mastery also supports scoring in linked concepts like fluid pressure and fluid energy calculations, a recurring theme in JEE practice sets. Always connect answers to the physical meaning of spewed velocity and review pitfalls before attempting exam problems.
FAQs on Torricelli's Theorem Explained with Derivation, Formula & Examples
1. What is Torricelli's theorem in physics?
Torricelli's theorem in physics states that the speed of efflux (flow speed) of a liquid out of an orifice under gravity is equal to the speed that a body would acquire falling freely from the same height.
Key points:
- The formula is v = √(2gh), where v is the velocity, g is gravity, and h is the height of liquid above the opening.
- It explains how fast a liquid exits through an orifice due to gravity.
- This law connects the principles of fluid mechanics and is based on Bernoulli's theorem.
2. How is Torricelli’s law derived from Bernoulli’s theorem?
Torricelli’s law is derived using Bernoulli's theorem by comparing pressure and velocity at the liquid surface and at the orifice:
- Apply Bernoulli’s equation between the open surface and the orifice at depth h below it.
- Assume atmospheric pressure acts at both points; ignore surface velocity (large tank).
- Equate pressure-energy terms and solve for efflux speed: v = √(2gh).
- This method uses fluid statics, hydrostatic pressure, and kinetic energy relations.
3. What did Torricelli's experiment prove?
Torricelli's experiment demonstrated that the velocity of fluid flowing out of an orifice depends only on the height of the fluid above it.
- He showed liquid flows as if it were falling freely from the top surface height.
- This was experimentally verified by matching the velocity using falling objects.
- It confirmed the relationship v = √(2gh) and supported Bernoulli's principle.
- The experiment forms the foundation of many fluid mechanics applications.
4. What is the formula for speed of efflux according to Torricelli's law?
The formula given by Torricelli's law for the speed of efflux is v = √(2gh).
- v: velocity of liquid leaving the orifice
- g: acceleration due to gravity (9.8 m/s²)
- h: vertical height of liquid surface above the orifice
5. What are real-life applications of Torricelli’s theorem?
Real-life applications of Torricelli’s theorem include:
- Designing water tanks and reservoirs for cities and agriculture
- Predicting flow from holes in dams or containers
- Calculating discharge in fountains and fire hoses
- Used in fluid mechanics calculations in engineering
- Determining leak rates in industrial and laboratory settings
6. What is the difference between Torricelli's theorem and Bernoulli's theorem?
Torricelli's theorem is a specific application of Bernoulli’s theorem.
- Bernoulli’s theorem explains energy conservation for fluids in motion.
- Torricelli’s theorem is derived by applying Bernoulli to an orifice in a tank, focusing on efflux velocity.
- Torricelli gives an exact formula (v = √(2gh)) for outflow speed, while Bernoulli is more general.
7. How do you use Torricelli’s theorem in numerical problems?
To use Torricelli's theorem in numericals:
- Identify the height h of liquid above the orifice.
- Use g = 9.8 m/s² if not otherwise mentioned.
- Insert values into the formula v = √(2gh).
- Calculate the speed or use it to find time/volume as required.
- Always check units for consistency in JEE or board exams.
8. Is atmospheric pressure considered in Torricelli's derivation?
Yes, atmospheric pressure is included but cancels out in most derivations because:
- Atmospheric pressure acts on both the tank surface and the orifice exit.
- This allows it to be omitted in the calculation, simplifying the formula to v = √(2gh).
- Only the pressure difference due to liquid height matters in the final result.
9. Can Torricelli's theorem be applied to viscous fluids or gases?
Torricelli's theorem assumes non-viscous (ideal) liquids and neglects fluid friction.
- For viscous fluids, energy losses mean actual velocity will be less than predicted.
- It does not directly apply to gases because their density and compressibility affect flow rate.
- Correcting factors are needed for real fluids as covered in advanced fluid mechanics.
10. What common mistakes do students make in Torricelli's law numericals?
Common student mistakes when applying Torricelli's law include:
- Using the wrong value or unit for g or h
- Forgetting to convert cm to m for height
- Not properly identifying the orifice height above the ground
- Ignoring the assumption of a large tank (surface velocity zero)
- Confusing efflux velocity with horizontal range in projectile motion
11. How does Torricelli’s theorem relate to the speed of efflux?
Torricelli’s theorem gives the direct mathematical relationship for the speed of efflux:
- The efflux speed (v = √(2gh)) tells you how fast liquid exits an orifice under gravity.
- The result is based on energy conversion from potential to kinetic energy.
- This law is used in fluid flow problems and real-life engineering designs.






















