




Range Formula for Projectile Motion on Inclined Surface with Stepwise Derivation
The study of projectile motion on inclined plane is crucial for JEE Main aspirants, as it combines concepts of 2D motion and vector decomposition in physics. This topic often appears in competitive exams, mirroring real-life scenarios like cricket balls bouncing uphill or missiles fired on mountain slopes. By understanding the underlying principles and formulas for such cases, you gain confidence in solving both direct numericals and conceptual problems tested in the exam.
A projectile on an inclined surface behaves differently than one projected onto flat ground. The inclination changes its range, time of flight, and trajectory path, making its study more challenging and interesting for physics students. You’ll often need to resolve velocities, carefully handle coordinate systems, and be alert for sign convention errors—common pitfalls for even well-prepared examinees.
Projectile Motion on Inclined Plane: Concepts and Key Equations
For projectile motion on inclined plane, always define your axes: usually, one axis is chosen parallel to the incline. Assume the projectile is thrown with speed u making angle θ with the horizontal, onto a plane inclined at α with respect to the horizontal. Gravity (g) acts vertically downwards.
When you work with numeric and symbolic cases, ensure you clearly resolve velocity components and use correct trigonometric identities to avoid errors in formulas and results.
- Initial velocity (u): Speed at which the body is projected.
- Angle θ: With respect to horizontal axis.
- Incline angle α: Slope with respect to horizontal.
- g: Acceleration due to gravity (9.8 m/s2 or 10 m/s2 for JEE).
- Range (R): Distance along the inclined surface where the projectile lands.
- Time of flight (T): Total air-time before striking incline.
| Quantity | Formula on Inclined Plane | Units |
|---|---|---|
| Range (R) | [2u2 cosθ sin(θ−α)] / [g cos2α] | metre (m) |
| Time of flight (T) | [2u sin(θ−α)] / [g cosα] | second (s) |
| Maximum height (H) | (u2 sin2θ)/(2g cos2α) | metre (m) |
For reference, revise general projectile motion, and study equations of motion for kinematics essentials. Using these, you can understand the subtle differences between flat ground and sloped projections.
Derivation of Range for Projectile Motion on Inclined Plane
Let’s derive the inclined-plane range formula step by step, a favorite JEE Main conceptual and formula-based problem.
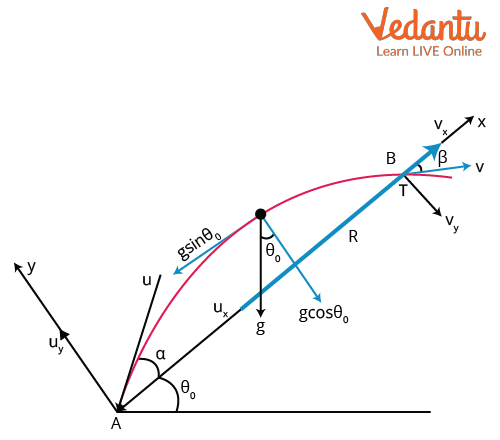
1. Split the initial velocity u into x and y components—horizontal and vertical to the ground.
2. Write the usual projectile equations for x and y positions as functions of time (t):
- x = u cosθ·t
- y = u sinθ·t − (1/2)gt2
3. The projectile lands when y = x tanα (where y is vertical and x is horizontal displacement, tanα is the inclination slope). Set this condition and solve for t = T.
4. Substitute x and y above into y = x tanα, rearrange the terms, and isolate t using algebraic manipulation.
5. Solve for time of flight (T):
- T = [2u sin(θ−α)] / [g cosα]
6. Use x = u cosθ·T to get the range R along the horizontal, and then relate it to the slope. Apply a little trigonometry to derive the expression for actual range along the inclined surface:
R = [2u2 cosθ sin(θ−α)] / [g cos2α] is the derived formula used in most JEE problems on projectiles on inclines.
When θ = α, range becomes zero as the projectile moves along the incline’s surface. For θ < α, the projectile lands behind the thrower on the slope. For θ > α, it lands ahead.
To visualize, check related diagrams in motion in 2D dimensions and equation of trajectory derivation.
Numerical Example: Solving a Projectile on Inclined Plane Question
Let’s solve a classic JEE Main-style numerical using the inclined range formula.
Question: A stone is projected from the foot of a hill (inclined at 30° to horizontal), with speed u = 20 m/s, making an angle θ = 45° from horizontal. Find the range along the incline. (Take g = 10 m/s2).
Stepwise Solution:
- Given u = 20, θ = 45°, α = 30°, g = 10.
- Find sin(θ−α) = sin(45°−30°) = sin(15°) ≈ 0.2588.
- cosθ = cos45° = 0.7071; cosα = cos30° = 0.8660.
- Plug into formula:
R = [2 × (20)2 × 0.7071 × 0.2588] / [10 × (0.8660)2] - Numerator: 2 × 400 × 0.7071 × 0.2588 ≈ 146.27
- Denominator: 10 × 0.7498 ≈ 7.498
- Final Range R = 146.27 / 7.498 ≈ 19.5 m
So, the projectile lands at a range of 19.5 m along the inclined plane.
Try making similar calculations for varying projection angles. For more problems, visit kinematics practice paper and kinematics mock test 2 sections.

Common Mistakes in Projectile Motion on Inclined Plane for JEE
Mastering projectile motion on inclined plane means avoiding certain conceptual and mathematical traps, especially during the fast pace of JEE exams.
- Mixing up θ and α: Never interchange projection and incline angles.
- Incorrect velocity components: Always resolve along axes parallel and perpendicular to the incline.
- Misapplying sign convention for gravity or initial velocity.
- Forgetting to use cos²α in the denominator of the range formula.
- Ignoring units or trigonometric values, leading to calculation errors.
Check related errors in kinematics revision notes and get tips from physics preparation tips for stress-free problem solving.
Application and Practice: Extend Your Learning on Projectile Motion on Inclined Plane
This topic models many real-world events, from military ballistics to athletes’ throws on hilly tracks. Practising a wide set of problems builds confidence for JEE Main—especially for maximum range, trajectory analysis, and variable angles.
- Sports: Balls projected upwards or downwards in games on slopes.
- Engineering: Calculating correct angles for civil structures on hilly terrains.
- Physics Olympiads: Advanced problems use vector techniques on inclines.
- Research: Simulation of projectiles on irregular surfaces.
Revise these by exploring motion in one dimension basics, or study angle of repose and vector resolution methods for further depth.
Download unsolved exercises (PDF) from the relevant modules or see JEE Main’s physics question paper section to test yourself. Revisiting topic summaries on Vedantu ensures you are aligned with the latest exam pattern and clear in concepts for all JEE projectile motion scenarios.
FAQs on Projectile Motion on an Inclined Plane: Concepts, Formulas & Applications
1. What is the formula for the range of a projectile on an inclined plane?
The range (R) of a projectile on an inclined plane is given by:
R = [2u² cos θ sin(θ - α)] / [g cos² α]
where:
• u = initial velocity
• θ = angle of projection with the horizontal
• α = angle of inclination of the plane
• g = acceleration due to gravity
This formula helps solve exam numericals on projectiles launched on or to inclined surfaces.
2. How do you derive the equation of motion for a projectile on an inclined plane?
To derive the equation of motion for a projectile on an inclined plane:
- Resolve initial velocity into components parallel and perpendicular to the inclined plane using vector decomposition.
- Use kinematic equations for each direction, considering the angle of inclination α.
- Eliminate time to obtain the trajectory equation in terms of x and y coordinates (or along and perpendicular to the incline).
This stepwise process allows calculation of path, time of flight, and range on an inclined surface for JEE and board exams.
3. What is the direction of the acceleration of a projectile on an inclined plane?
The acceleration of a projectile on an inclined plane is always vertically downward due to gravity (g), regardless of the plane's inclination. It does not change direction with respect to the incline, even though velocity components are resolved using the inclined axis for calculation simplicity.
- Gravity acts vertically downwards.
- Components of motion are analyzed along and perpendicular to the inclined plane.
4. What is the equation for projectile motion at an angle?
The general equation for projectile motion when launched at an angle θ with the horizontal is:
- Range: R = (u² sin 2θ) / g (for horizontal surface)
- Time of flight: T = (2u sin θ) / g
- Maximum height: H = (u² sin² θ) / (2g)
For an inclined plane, the angle is adjusted, and the range formula changes as per the incline's orientation.
5. How does the angle of inclination affect the range of a projectile?
The inclination angle (α) changes the projectile's range by altering the effective gravity component and the projection direction. Range is maximized for a specific combination of projection angle (θ) and incline angle (α):
- As the inclination increases up the slope, the range decreases for the same initial velocity.
- Range is calculated using the modified formula for inclines.
Choosing the correct projection angle is essential to achieve maximum range on inclined planes.
6. What is the difference between projectile motion on a horizontal and an inclined plane?
The key difference is the landing surface orientation:
- Horizontal plane: The range uses R = (u² sin 2θ)/g and the trajectory is symmetric.
- Inclined plane: The effective acceleration and displacement components change; the range formula is adjusted for the angle of inclination α.
On inclines, students must carefully resolve velocities and distances along and perpendicular to the slope for correct answers in board and JEE exams.
7. Can projectile motion on an incline appear in JEE Main or Advanced numericals?
Yes, projectile motion on inclined planes is a popular and exam-relevant topic for JEE Main and Advanced numericals. Students should:
- Know all inclined plane projectile formulas.
- Practice derivations and variety of numerical problems (up and down inclines).
- Review vector resolution and direction conventions for exam accuracy.
8. What common mistakes do students make with angles and directions in projectile motion on inclined planes?
Common student mistakes include:
- Confusing projection angle θ with inclination α.
- Using the horizontal range formula instead of the incline formula.
- Improper vector decomposition of velocity.
- Forgetting to use sin(θ - α) or sign conventions.
- Errors in trigonometric calculations and direction (up the incline vs. down).
Careful diagram analysis and stepwise problem-solving are crucial for correct answers in exams.
9. What happens if the projection angle and incline angle are the same?
If projection angle θ = inclination angle α: The value sin(θ - α) = 0, meaning the range (R) becomes zero. The projectile lands immediately on the incline at the same spot it was projected, showing the sensitivity of the formula to these angles.
10. Can you use the same formula for projectiles launched down the incline?
The range formula applies for both up and down incline launches, but always ensure:
- Use the correct sign and direction for (θ - α) in sin(θ - α).
- For downward launches, θ is measured below the horizontal (or negative relative to the incline).
Always sketch the scenario before applying the formula in JEE or board numericals.


































