




What is Two-Dimensional Motion? Definition, Formulas & Applications
Understanding Motion in 2d Dimensions is essential for JEE Main Physics, as many real-life and exam-centric motions involve simultaneous movement along x and y axes. In such cases, the object's position changes in a plane, and both horizontal and vertical components must be analyzed together to compute displacement, velocity, and acceleration accurately.
Two-dimensional motion includes scenarios like a ball thrown at an angle, a car turning on a curved road, or a bullet fired at an incline. Compared to one-dimensional motion, it uses vectors for representing direction and magnitude, making vector addition, decomposition, and graphical representation core skills for problem solving.
Differences Between 1D, 2D, and 3D Motion
| Parameter | 1D Motion | 2D Motion | 3D Motion |
|---|---|---|---|
| Position changes along | x (or y) only | x and y axes | x, y, and z axes |
| Graph | Straight line | Plane curve | Space curve |
| Example | A car in a lane | Projectile motion | Bird flying freely |
In Motion in 2d Dimensions, vectors are fundamental since each motion parameter (displacement, velocity, acceleration) is described using both magnitude and direction. Understanding how to represent and combine vectors is crucial for JEE questions involving trajectories and resultant motion.
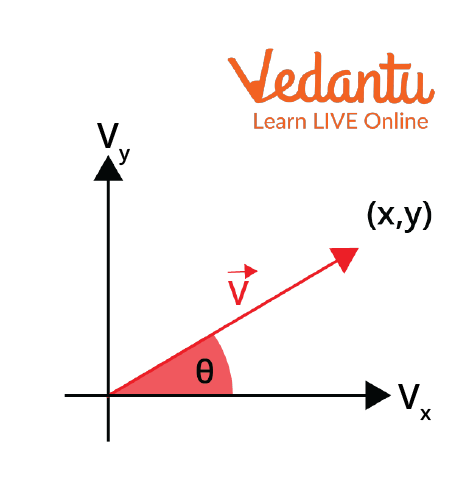
Displacement in 2D is the straight-line vector from the initial to the final position. Velocity and acceleration are also vectors, each with x and y components. For example, if position vector is r = x̂ + yĵ, then velocity vector is v = vx̂ + vyĵ, where vx and vy are components along x and y.
Equations and Formulas for Motion in 2d Dimensions
In Motion in 2d Dimensions, each motion is resolved along x and y axes, using independent kinematic equations. This enables calculation of position, velocity, and time for each direction separately before combining them for the resultant motion.
| Quantity | x-direction | y-direction |
|---|---|---|
| Displacement (s) | sx = ux t + ½ axt2 | sy = uy t + ½ ayt2 |
| Velocity (v) | vx = ux + axt | vy = uy + ayt |
| Resultant speed | v = √(vx2 + vy2) | |
Always treat acceleration independently along each axis unless a problem states otherwise. Resolve initial velocity and acceleration components with trigonometric functions for angles.
Projectile Motion as a Key Example of 2D Motion
Projectile motion demonstrates motion in 2d dimensions, where an object is launched at an angle θ with an initial speed u. The only acceleration present is gravity (g), acting vertically downward, making x and y motions independent.
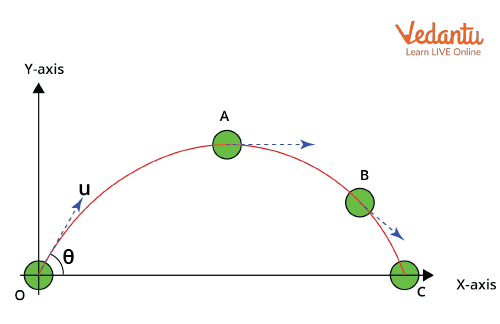
The horizontal velocity remains constant (ux = u cosθ), while the vertical velocity changes due to gravity (uy = u sinθ, ay = -g). The classic equations are:
- Horizontal displacement: sx = (u cosθ) t
- Vertical displacement: sy = (u sinθ) t - ½gt2
- Maximum height: H = u2 sin2θ / (2g)
- Time of flight: T = 2u sinθ / g (see derivation)
- Range: R = u2 sin2θ / g
For full steps, explore projectile motion details and equation of trajectory derivation on Vedantu.
Solved Examples: Motion in 2d Dimensions
Reviewing classic problems sharpens your numerical skills in 2D motion. Each requires resolving vectors and applying equations for each axis.
- A ball is projected with u = 20 m/s at 30°. Find the range and maximum height.
- Given: u = 20 m/s, θ = 30°, g = 9.8 m/s²
- Range R = u2sin2θ/g = 400 × 0.5 / 9.8 ≈ 20.4 m
- Max height H = u2sin2θ/(2g) ≈ 400 × 0.25 / 19.6 ≈ 5.1 m
- Resolve components: ux = 20 × cos30° ≈ 17.32 m/s, uy = 20 × sin30° = 10 m/s
- At maximum height, vertical velocity vy = 0; find time to reach H by vy = uy - gt = 0 → t = uy/g ≈ 1.02 s
Practice more with the Motion in 2d Dimensions worksheet and cross-check your solutions.
Common Mistakes and Fast Revision Tips
- Forgetting to resolve velocity and acceleration into x and y components.
- Assuming acceleration acts in both directions; in projectile motion, ax = 0.
- Combining final answers without using vector addition for resultant quantities.
- Ignoring units or sign (especially for vertical direction).
- Not drawing a motion diagram before calculations.
- Use trigonometric functions correctly for components.
- Check if acceleration is constant before using kinematic formulas.
- Always visualize vectors and label axes on diagrams.
- Practice numericals from multiple JEE question papers.
JEE Applications and Advanced Topics
Mastering Motion in 2d Dimensions is necessary for tackling river-boat, airplane-crosswind, oblique collision, and advanced projectile questions in JEE Main and Advanced. Building intuition for vector resolution, signs, and independent axis analysis unlocks high-scoring problems. For a deep dive, study vectors in JEE Physics and related advanced topics below.
- Motion in One Dimension
- Projectile Motion
- Time of Flight
- Relative Motion
- Rotational Motion
- Laws of Motion
Stay consistent with regular practice, and refer to trusted resources like Vedantu and standard textbooks. For expert guidance, check out more JEE-centric motion and kinematics solutions across the platform.
FAQs on Motion in 2D Dimensions: Complete Physics Guide
1. What is two-dimensional motion in physics?
Two-dimensional motion refers to the movement of an object in a plane, having components of displacement and velocity in both the x and y directions. Key features include:
- Motion occurs simultaneously along two axes (horizontal and vertical).
- Examples include projectile motion, circular motion in a plane, and the movement of a car taking a curved path.
- Requires using vector addition and component analysis for solving problems.
2. How do you calculate velocity and displacement in 2D motion?
Velocity and displacement in two-dimensional motion are calculated by resolving the motion into x and y components and then applying vector addition. Key steps:
- Find the x and y parts using formulas: vx = ux + axt and vy = uy + ayt
- Total velocity: v = √(vx2 + vy2)
- Displacement: s = √(sx2 + sy2)
- Use vector diagrams to combine and visualise these quantities accurately.
3. What are some real-life examples of motion in two dimensions?
Typical examples of two-dimensional motion include:
- Projectile motion (ball thrown at an angle)
- Car taking a curved turn on a racetrack
- Uniform circular motion in a horizontal plane
- Aircraft following a curved flight path
4. What is the main formula used for 2D motion problems?
The main formulas for 2D motion problems extend the standard kinematics equations into two axes:
- x direction: sx = uxt + 0.5 axt2
- y direction: sy = uyt + 0.5 ayt2
- Combine components: Resultant displacement or velocity = √(componentx2 + componenty2)
5. Why is projectile motion considered two-dimensional motion?
Projectile motion is considered two-dimensional because the object moves horizontally (x-axis) and vertically (y-axis) at the same time. Key reasons:
- It involves two independent components: uniform motion along x and accelerated motion (due to gravity) along y.
- The path traced (parabola) depends on both directions.
- Formulas require calculation of both horizontal and vertical positions together using 2D equations.
6. What is the difference between one-dimensional, two-dimensional, and three-dimensional motion?
The difference lies in the number of axes the object moves along:
- One-dimensional (1D): Movement along a single axis (x or y) only.
- Two-dimensional (2D): Movement happens in a plane, covering both x and y axes (e.g., projectile motion).
- Three-dimensional (3D): Movement occurs along x, y, and z axes (e.g., movement of a drone in space).
7. Can 2D motion always be broken into independent x and y components?
Yes, in classical physics, two-dimensional motion can be resolved into independent x and y components if the forces or accelerations are constant and act independently along each axis. This allows for:
- Solving each direction separately using standard equations.
- Applying vector decomposition for displacement, velocity, and acceleration.
8. What are the common mistakes students make in 2D motion problems?
Common mistakes include:
- Not resolving vectors into x and y components correctly.
- Using direct addition instead of the Pythagorean theorem for resultant values.
- Confusing magnitude with direction in vector answers.
- Forgetting to use the correct formula for each axis.
- Neglecting unit consistency and angle reference directions.
9. Is uniform circular motion also a type of two-dimensional motion?
Yes, uniform circular motion is a key example of two-dimensional motion, where the object moves with constant speed along a circle in a plane. Characteristics are:
- Constant magnitude of velocity, but changing direction.
- Motion is confined to two axes (usually x and y) forming a circle.
- Acceleration (centripetal) always points towards the centre of the path.
10. How does neglecting air resistance affect 2D motion problems?
Neglecting air resistance in two-dimensional motion problems simplifies calculations by allowing you to:
- Assume constant acceleration due to gravity in the vertical direction only.
- Treat horizontal velocity as constant (no opposing forces).
- Apply standard kinematic equations without needing drag force adjustments.
























