
What is the critical angle ?
Answer
465k+ views
Hint: We use the concept of refraction of light for denser medium to rarer medium and how does light bend for incidence of light from denser medium to rarer medium and also study about total internal reflection. Total internal reflection happens when light rays come from denser medium to rarer medium from a certain angle.
Formula used:
Snell’s law of refraction is given by,
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}}\]
where, \[i\] is the angle of incidence \[r\] is the angle of refraction, \[{n_1}\] is the absolute refractive index of first medium and \[{n_2}\] is the refractive index of second medium.
Complete step by step answer:
If a ray of light goes from denser medium to rarer medium there is a certain angle above which if a light ray is incident then the light ray does not get refracted rather its bends totally and comes back to the denser medium again or reflection happens. This phenomenon is called total reflection of light.
In optics, the smallest angle of incidence beyond which if a light ray is incident from denser medium to rarer medium that causes the total internal reflection of light is known as the critical angle.
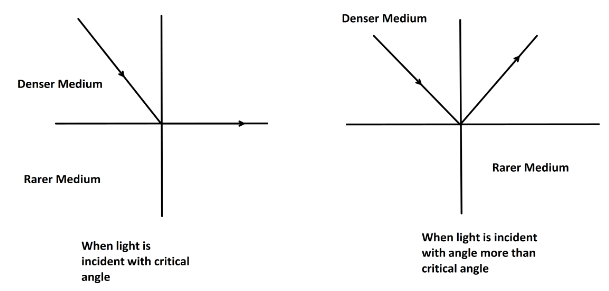
For, incident ray of light at a critical angle the refracted ray passes through the boundary of the denser and rarer medium. So, angle of refraction is \[{90^ \circ }\].Hence, from Snell’s law we can write,
\[\dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{\sin {i_c}}}{{\sin {{90}^ \circ }}}\]
\[{i_c}\] is the angle of incidence or critical angle and angle of refraction is \[{90^ \circ }\].
\[\sin {i_c} = \dfrac{{{n_2}}}{{{n_1}}}\]
\[\therefore {i_c} = {\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)\]
This is the mathematical expression for critical angle.
Note: Total internal takes place when only the angle of incidence is greater than critical angle. If the angle of incidence is less than or equal to the critical angle total internal reflection does not take place. Property of total internal reflection is used to make optical fibre which is heavily used in broadband connections now. This property is also used to make mirrors, since in total reflection the total light gets reflected to the denser medium but in a normal mirror some of the light gets refracted so intensity of the emergent ray becomes lesser than the original.
Formula used:
Snell’s law of refraction is given by,
\[\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}}\]
where, \[i\] is the angle of incidence \[r\] is the angle of refraction, \[{n_1}\] is the absolute refractive index of first medium and \[{n_2}\] is the refractive index of second medium.
Complete step by step answer:
If a ray of light goes from denser medium to rarer medium there is a certain angle above which if a light ray is incident then the light ray does not get refracted rather its bends totally and comes back to the denser medium again or reflection happens. This phenomenon is called total reflection of light.
In optics, the smallest angle of incidence beyond which if a light ray is incident from denser medium to rarer medium that causes the total internal reflection of light is known as the critical angle.

For, incident ray of light at a critical angle the refracted ray passes through the boundary of the denser and rarer medium. So, angle of refraction is \[{90^ \circ }\].Hence, from Snell’s law we can write,
\[\dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{\sin {i_c}}}{{\sin {{90}^ \circ }}}\]
\[{i_c}\] is the angle of incidence or critical angle and angle of refraction is \[{90^ \circ }\].
\[\sin {i_c} = \dfrac{{{n_2}}}{{{n_1}}}\]
\[\therefore {i_c} = {\sin ^{ - 1}}\left( {\dfrac{{{n_2}}}{{{n_1}}}} \right)\]
This is the mathematical expression for critical angle.
Note: Total internal takes place when only the angle of incidence is greater than critical angle. If the angle of incidence is less than or equal to the critical angle total internal reflection does not take place. Property of total internal reflection is used to make optical fibre which is heavily used in broadband connections now. This property is also used to make mirrors, since in total reflection the total light gets reflected to the denser medium but in a normal mirror some of the light gets refracted so intensity of the emergent ray becomes lesser than the original.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

Give 10 examples of unisexual and bisexual flowers

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?

How many single covalent bonds can nitrogen form class 12 chemistry CBSE

The idea of the Constitution of India was first of class 12 social science CBSE

What is the feedback mechanism of hormone regulation class 12 biology CBSE




