
We know that $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$ , so verify this identity for $\theta =30{}^\circ $ .
Answer
567k+ views
Hint: To solve the above question, you need to individually solve the right-hand side and left-hand side of the equation individually by putting the required values and show that both sides of the equation are equal. For putting the required values you need to use the trigonometric ratio table contains the values of different trigonometric ratios for trigonometric standard angles such as $0{}^\circ ,30{}^\circ ,45{}^\circ ,60{}^\circ \text{ and 90}{}^\circ $ .
Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.
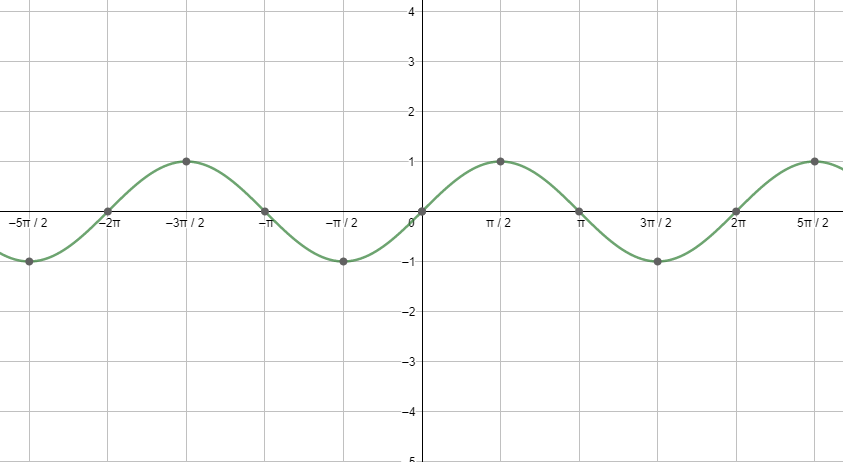
Next, let us see the graph of cosx.
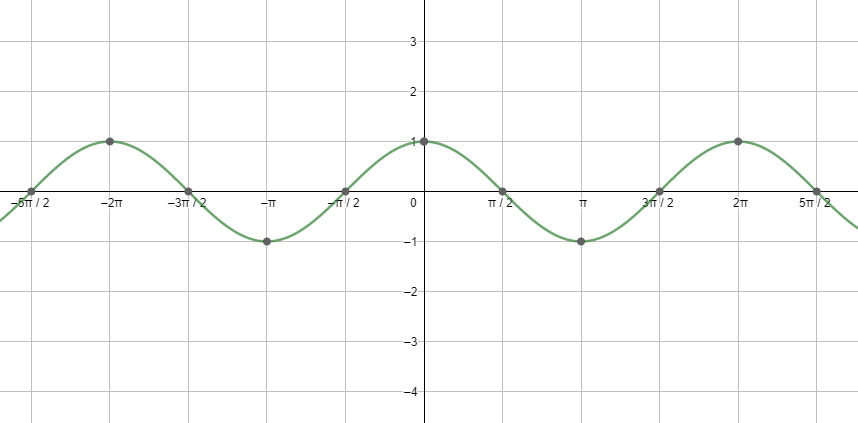
Looking at both the graphs, and using the relations between the different trigonometric ratios, we get
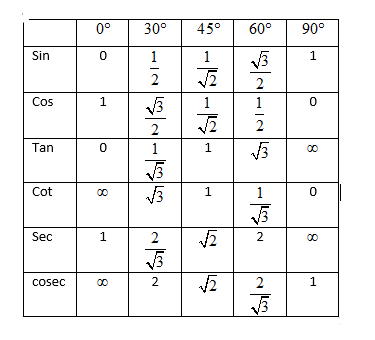
Let us start the solution to the above question by simplifying the left-hand side of the equation $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$ by putting the value $\theta =30{}^\circ $ .
$\sin 2\theta $
$=\sin \left( 2\times 30{}^\circ \right)$
$=\sin 60{}^\circ $
And we know that the value of $\sin 60{}^\circ $ is equal to $\dfrac{\sqrt{3}}{2}$ . So, we get
$=\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$
So, the left-hand side of the equation $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$ is equal to $\dfrac{\sqrt{3}}{2}$ .
Now let us simplify the right-hand side of the equation by putting the values $\theta =30{}^\circ $ .
$\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$
$=\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$
Now we know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$ .
$=\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$
$=\dfrac{2\left( \dfrac{1}{\sqrt{3}} \right)}{1+{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}}$
$=\dfrac{\dfrac{2}{\sqrt{3}}}{1+\dfrac{1}{3}}=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{4}{3}}=\dfrac{\sqrt{3}}{2}$
Therefore, we can say that the left-hand side of the equation $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$ is equal to the right-hand side. So, we have verified the above equation.
Note: Be careful while putting the values of the different trigonometric ratios in the expression for solving the question as the values of different trigonometric ratios are really confusing and there is always a possibility that you may get confused and put $\sin 30{}^\circ =\dfrac{\sqrt{3}}{2}\text{ and sin60}{}^\circ \text{=}\dfrac{1}{2}$ , which is wrong.
Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

Next, let us see the graph of cosx.

Looking at both the graphs, and using the relations between the different trigonometric ratios, we get

Let us start the solution to the above question by simplifying the left-hand side of the equation $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$ by putting the value $\theta =30{}^\circ $ .
$\sin 2\theta $
$=\sin \left( 2\times 30{}^\circ \right)$
$=\sin 60{}^\circ $
And we know that the value of $\sin 60{}^\circ $ is equal to $\dfrac{\sqrt{3}}{2}$ . So, we get
$=\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$
So, the left-hand side of the equation $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$ is equal to $\dfrac{\sqrt{3}}{2}$ .
Now let us simplify the right-hand side of the equation by putting the values $\theta =30{}^\circ $ .
$\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$
$=\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$
Now we know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$ .
$=\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$
$=\dfrac{2\left( \dfrac{1}{\sqrt{3}} \right)}{1+{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}}$
$=\dfrac{\dfrac{2}{\sqrt{3}}}{1+\dfrac{1}{3}}=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{4}{3}}=\dfrac{\sqrt{3}}{2}$
Therefore, we can say that the left-hand side of the equation $\sin 2\theta =\dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta }$ is equal to the right-hand side. So, we have verified the above equation.
Note: Be careful while putting the values of the different trigonometric ratios in the expression for solving the question as the values of different trigonometric ratios are really confusing and there is always a possibility that you may get confused and put $\sin 30{}^\circ =\dfrac{\sqrt{3}}{2}\text{ and sin60}{}^\circ \text{=}\dfrac{1}{2}$ , which is wrong.
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Why is Sardar Vallabhbhai Patel called the Iron man class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




