
Verify the identity $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ for the value $\theta =30{}^\circ $ .
Answer
561k+ views
Hint: The values of trigonometric ratios of standard angles are known to us from the trigonometric tables. Using the trigonometric table substitute the values of $\cos 90{}^\circ =0\text{ and cos30}{}^\circ \text{=}\dfrac{\sqrt{3}}{2}$ in the expressions that you get after substituting $\theta =30{}^\circ $ in the RHS and the LHS of the equation given in the question. If the values that you get from the RHS and the LHS are equal, you can say that you have verified the equation.
Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.
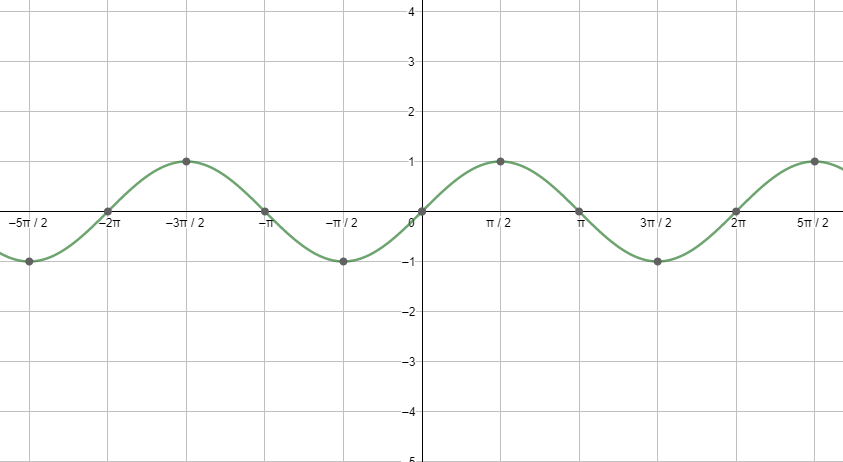
Next, let us see the graph of cosx.
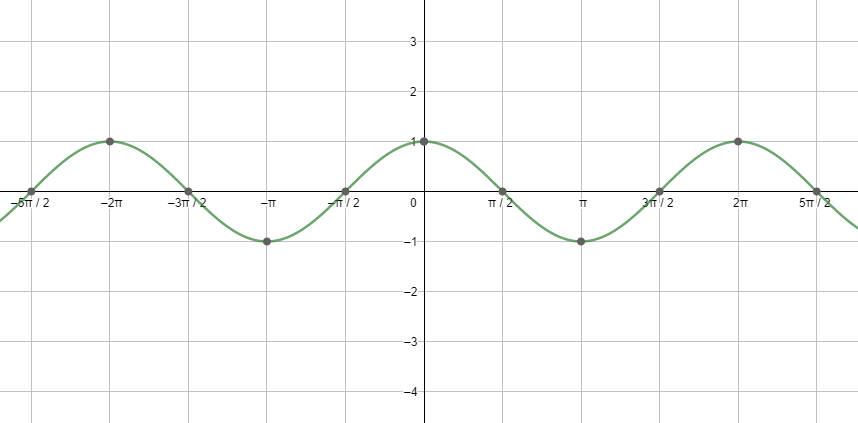
Looking at both the graphs, and using the relations between the different trigonometric ratios, we get
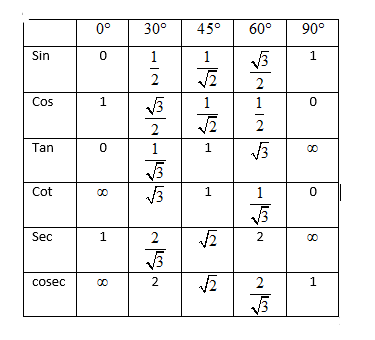
Let us start the solution to the above question by simplifying the left-hand side of the equation $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ by putting the value $\theta =30{}^\circ $ .
$\cos 3\theta $
$=\cos \left( 3\times 30{}^\circ \right)$
$=\cos 90{}^\circ $
And we know that the value of $\cos 90{}^\circ $ is equal to 0. So, we get
$=\cos 90{}^\circ =0$
So, the left-hand side of the equation $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ is equal to $0$ .
Now let us simplify the right-hand side of the equation by putting the values $\theta =30{}^\circ $ .
$4{{\cos }^{3}}\theta -3\cos \theta $
$=4{{\cos }^{3}}30{}^\circ -3\cos 30{}^\circ $
Now we know that $\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}$ .
$=4{{\cos }^{3}}30{}^\circ -3\cos 30{}^\circ $
$=4\times {{\left( \dfrac{\sqrt{3}}{2} \right)}^{3}}-3\times \dfrac{\sqrt{3}}{2}$
$=\dfrac{\sqrt{3}}{2}\left( 4\times \dfrac{3}{4}-3 \right)=0$
Therefore, we can say that the left-hand side of the equation $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ is equal to the right-hand side. So, we have verified the above equation.
Note: It is generally seen that students are very confused in the values of $\sin 30{}^\circ ,\sin 60{}^\circ ,\cos 30{}^\circ \text{ and cos60}{}^\circ $ and very frequently make mistakes in their values. So, it is very important that you thoroughly learn the trigonometric table and properties related to complementary angles and specially the values of $\sin 30{}^\circ ,\sin 60{}^\circ ,\cos 30{}^\circ \text{ and cos60}{}^\circ $ .
Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

Next, let us see the graph of cosx.

Looking at both the graphs, and using the relations between the different trigonometric ratios, we get

Let us start the solution to the above question by simplifying the left-hand side of the equation $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ by putting the value $\theta =30{}^\circ $ .
$\cos 3\theta $
$=\cos \left( 3\times 30{}^\circ \right)$
$=\cos 90{}^\circ $
And we know that the value of $\cos 90{}^\circ $ is equal to 0. So, we get
$=\cos 90{}^\circ =0$
So, the left-hand side of the equation $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ is equal to $0$ .
Now let us simplify the right-hand side of the equation by putting the values $\theta =30{}^\circ $ .
$4{{\cos }^{3}}\theta -3\cos \theta $
$=4{{\cos }^{3}}30{}^\circ -3\cos 30{}^\circ $
Now we know that $\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}$ .
$=4{{\cos }^{3}}30{}^\circ -3\cos 30{}^\circ $
$=4\times {{\left( \dfrac{\sqrt{3}}{2} \right)}^{3}}-3\times \dfrac{\sqrt{3}}{2}$
$=\dfrac{\sqrt{3}}{2}\left( 4\times \dfrac{3}{4}-3 \right)=0$
Therefore, we can say that the left-hand side of the equation $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ is equal to the right-hand side. So, we have verified the above equation.
Note: It is generally seen that students are very confused in the values of $\sin 30{}^\circ ,\sin 60{}^\circ ,\cos 30{}^\circ \text{ and cos60}{}^\circ $ and very frequently make mistakes in their values. So, it is very important that you thoroughly learn the trigonometric table and properties related to complementary angles and specially the values of $\sin 30{}^\circ ,\sin 60{}^\circ ,\cos 30{}^\circ \text{ and cos60}{}^\circ $ .
Recently Updated Pages
A number is selected from numbers 1 to 25 The probability class 10 maths CBSE

A bag contains 12 blue balls and x red balls If one class 10 maths CBSE

If the probability of winning a game is dfrac511 what class 10 maths CBSE

There are 20 cylindrical pillars in a path The radius class 10 maths CBSE

Identify the kind of letter for which of the following class 10 english CBSE

Which of the following is not a laboratory safety rule class 10 chemistry CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




