
Two identical parallel plate capacitors are placed in series and connected to a constant voltage source \[{{V}_{o}}\] volt. If one of the capacitors is completely immersed in liquid with dielectric constant K, the potential difference between the plates of other capacitor will change to:
A. \[\left( \dfrac{K+1}{K} \right){{V}_{o}}\]
B. \[\left( \dfrac{K}{K+1} \right){{V}_{o}}\]
C. \[\left( \dfrac{K+1}{2K} \right){{V}_{o}}\]
D. \[\left( \dfrac{2K}{K+1} \right){{V}_{o}}\]
Answer
516.6k+ views
Hint: In this question we are asked to calculate the potential difference of a capacitor. It is given that other capacitor connected in series is later filled with dielectric with dielectric constant K. To solve this, we will assume the potential difference in the capacitor plates and later again calculate the potential difference when the dielectric is filed. We know that the charge in the circuit is conserved. Therefore, we will be using this to calculate our final answer.
Formula Used: -
\[{{V}_{1}}+{{V}_{2}}={{V}_{o}}\]
Where,
V is the potential difference
\[{{C}_{1}}{{V}_{1}}={{C}_{2}}{{V}_{2}}\]
Where,
C is the capacitance
Complete answer:
We know that potential difference in over circuit when the capacitors are connected in series is given by,
\[{{V}_{1}}+{{V}_{2}}={{V}_{o}}\] ……………………… (1)
\[{{V}_{1}}\] and \[{{V}_{2}}\] is the potential difference between the plates of capacitors as shown in the figure below,
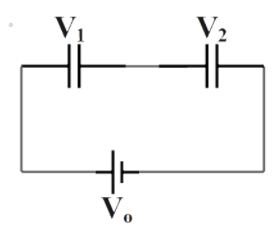
Now, we also know that the charge in both the capacitors will be equal and conserved. It can be given by,
\[{{C}_{1}}{{V}_{1}}={{C}_{2}}{{V}_{2}}\] ……………………. (2)
Now, assume that the capacitor 1 is filled with dielectric with dielectric constant K. We know the capacitance in both the capacitors is equal as they are said to be identical. Therefore, above equation will become,
\[KC{{V}_{1}}=C{{V}_{2}}\]
Therefore,
\[{{V}_{1}}=\dfrac{{{V}_{2}}}{K}\]
After substituting the above value in equation (1)
We get,
\[\dfrac{{{V}_{2}}}{K}+{{V}_{2}}={{V}_{o}}\]
Therefore,
\[{{V}_{2}}\left( 1+\dfrac{1}{K} \right)={{V}_{o}}\]
On solving,
We get,
\[{{V}_{2}}=\left( \dfrac{K}{K+1} \right){{V}_{o}}\]
Therefore, the correct answer is option B.
Note:
A capacitor is a device used to store the electric energy in an electric field. A capacitor works on the principle that the capacitance of the conductor increases when an earthed conductor is brought near it. We know that the positive and negative charges attract each other. The plates of the capacitor contain the opposite charged particles. This creates an electric field in between the plates. This is how a capacitor stores energy.
Formula Used: -
\[{{V}_{1}}+{{V}_{2}}={{V}_{o}}\]
Where,
V is the potential difference
\[{{C}_{1}}{{V}_{1}}={{C}_{2}}{{V}_{2}}\]
Where,
C is the capacitance
Complete answer:
We know that potential difference in over circuit when the capacitors are connected in series is given by,
\[{{V}_{1}}+{{V}_{2}}={{V}_{o}}\] ……………………… (1)
\[{{V}_{1}}\] and \[{{V}_{2}}\] is the potential difference between the plates of capacitors as shown in the figure below,

Now, we also know that the charge in both the capacitors will be equal and conserved. It can be given by,
\[{{C}_{1}}{{V}_{1}}={{C}_{2}}{{V}_{2}}\] ……………………. (2)
Now, assume that the capacitor 1 is filled with dielectric with dielectric constant K. We know the capacitance in both the capacitors is equal as they are said to be identical. Therefore, above equation will become,
\[KC{{V}_{1}}=C{{V}_{2}}\]
Therefore,
\[{{V}_{1}}=\dfrac{{{V}_{2}}}{K}\]
After substituting the above value in equation (1)
We get,
\[\dfrac{{{V}_{2}}}{K}+{{V}_{2}}={{V}_{o}}\]
Therefore,
\[{{V}_{2}}\left( 1+\dfrac{1}{K} \right)={{V}_{o}}\]
On solving,
We get,
\[{{V}_{2}}=\left( \dfrac{K}{K+1} \right){{V}_{o}}\]
Therefore, the correct answer is option B.
Note:
A capacitor is a device used to store the electric energy in an electric field. A capacitor works on the principle that the capacitance of the conductor increases when an earthed conductor is brought near it. We know that the positive and negative charges attract each other. The plates of the capacitor contain the opposite charged particles. This creates an electric field in between the plates. This is how a capacitor stores energy.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Which are the Top 10 Largest Countries of the World?

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Pomato is a Somatic hybrid b Allopolyploid c Natural class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE




